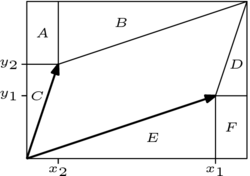
Man begründe anhand des Bildes, dass zu zwei Vektoren ${\displaystyle {}(x_{1},y_{1})}$ und ${\displaystyle {}(x_{2},y_{2})}$ die Determinante der durch die Vektoren definierten ${\displaystyle {}2\times 2}$-Matrix mit dem Flächeninhalt des von den beiden Vektoren aufgespannten Parallelogramms (bis auf das Vorzeichen) übereinstimmt.

${\displaystyle {}\,}$

Es seien ${\displaystyle {}P_{1}=(a_{1},b_{1}),\,P_{2}=(a_{2},b_{2})}$ und ${\displaystyle {}P_{3}=(a_{3},b_{3})}$ drei Punkte im ${\displaystyle {}\mathbb {R} ^{2}}$. Stelle den Flächeninhalt des zugehörigen Dreiecks mit ${\displaystyle {}a_{1},b_{1},a_{2},b_{2},a_{3},b_{3}}$ dar.

Berechne den Flächeninhalt des von den Vektoren

${\displaystyle (1,3,5){\text{ und }}(-2,4,1)}$

im ${\displaystyle {}\mathbb {R} ^{3}}$ erzeugten Parallelogramms (in dem von diesen Vektoren erzeugten Unterraum).

Zeige, dass die Determinante einer linearen Isometrie

${\displaystyle \varphi \colon \mathbb {R} ^{n}\longrightarrow \mathbb {R} ^{n}}$

gleich ${\displaystyle {}1}$ oder gleich ${\displaystyle {}-1}$ ist.

Es sei

${\displaystyle L\colon \mathbb {R} ^{n}\longrightarrow \mathbb {R} ^{n}}$

eine lineare Abbildung und ${\displaystyle {}c\in \mathbb {R} _{\geq 0}}$. Zeige die Gleichheit ${\displaystyle {}L_{*}(c\lambda ^{n})=c(L_{*}\lambda ^{n})}$.

Sei ${\displaystyle {}n\in \mathbb {N} }$. Zeige, dass es eine positive reelle Zahl ${\displaystyle {}\kappa _{n}}$ gibt derart, dass das ${\displaystyle {}n}$-dimensionale Volumen einer abgeschlossenen Kugel im ${\displaystyle {}\mathbb {R} ^{n}}$ mit Radius ${\displaystyle {}r}$ und mit einem beliebigen Mittelpunkt gleich ${\displaystyle {}\kappa _{n}r^{n}}$ ist.

Man gebe ein Beispiel für eine lineare Abbildung

${\displaystyle \varphi \colon \mathbb {R} ^{n}\longrightarrow \mathbb {R} ^{n}}$

derart, dass ${\displaystyle {}\varphi }$ volumentreu, aber keine Isometrie ist.

Es sei

${\displaystyle \varphi \colon \mathbb {R} ^{n}\longrightarrow \mathbb {R} ^{n}}$

ein linearer Endomorphismus, der nicht bijektiv sei. Zeige, dass das Bildmaß ${\displaystyle {}\varphi _{*}\lambda ^{n}}$ nicht ${\displaystyle {}\sigma }$-endlich ist.

Berechne das Volumen des von den Vektoren

${\displaystyle (2,1,3,4),(4,0,-1,3){\text{ und }}(5,-2,-2,0)}$

im ${\displaystyle {}\mathbb {R} ^{4}}$ erzeugten Parallelotops (in dem von diesen Vektoren erzeugten Unterraum).

Berechne den Flächeninhalt des von den Vektoren ${\displaystyle {}(0,1),\,(2,0),\,(1,3)}$ erzeugten „Pseudoparallelogramms“, also von

${\displaystyle S={\left\{a(0,1)+b(2,0)+c(1,3)\mid a,b,c\in [0,1]\right\}}.}$

Es sei

${\displaystyle \varphi \colon \mathbb {R} ^{n}\longrightarrow \mathbb {R} ^{m}}$

eine lineare Abbildung, die surjektiv, aber nicht injektiv sei. Zeige, dass das Bildmaß ${\displaystyle {}\mu =\varphi _{*}\lambda ^{n}}$ für jede Borelmenge ${\displaystyle {}T\subseteq \mathbb {R} ^{m}}$ durch

${\displaystyle \mu (T)={\begin{cases}0,{\text{ falls }}\lambda ^{m}(T)=0\,,\\\infty ,{\text{ falls }}\lambda ^{m}(T)>0\,,\end{cases}}}$

bestimmt ist.

Sei

${\displaystyle S={\left\{(x,y,z)\in \mathbb {R} ^{3}\mid x^{2}+y^{2}+z^{2}=1\right\}}}$

die Oberfläche der Einheitskugel. Zeige, dass das Volumen dieser Oberfläche ${\displaystyle {}0}$ ist.

Es sei ${\displaystyle {}u\in \mathbb {C} }$ eine komplexe Zahl mit ${\displaystyle {}\vert {u}\vert =1}$. Zeige, dass die Multiplikationsabbildung

${\displaystyle \mathbb {C} \longrightarrow \mathbb {C} ,\,z\longmapsto uz,}$

flächentreu ist.