Definiere die folgenden (kursiv gedruckten) Begriffe.

1. Der affine Raum.
2. Der Produktring zu kommutativen Ringen ${\displaystyle {}R_{1},\ldots ,R_{n}}$.
3. Ein ${\displaystyle {}K}$-wertiger Punkt zu einem kommutativen Monoid ${\displaystyle {}M}$.
4. Die Normalisierung eines Integritätsbereiches ${\displaystyle {}R}$.
5. Die Einbettungsdimension eines lokalen kommutativen noetherschen Ringes ${\displaystyle {}R}$.
6. Die Zariski-Topologie auf dem projektiven Raum ${\displaystyle {}{\mathbb {P} }_{K}^{n}}$.

Formuliere die folgenden Sätze.

1. Der Satz über die Noethersche Normalisierung für eine Kurve.
2. Die geometrische Version des Hilbertschen Basissatzes.
3. Der Satz über die Multiplizität für ein numerisches Monoid.

Berechne in

${\displaystyle \mathbb {Z} /(7)[X]/(X^{3}+4X^{2}+X+5)}$

${\displaystyle (2x^{2}+5x+3)\cdot (3x^{2}+x+6)}$

(${\displaystyle {}x}$ bezeichne die Restklasse von ${\displaystyle {}X}$).

Es ist

${\displaystyle {}x^{3}=3x^{2}+6x+2\,}$

und

${\displaystyle {}{\begin{aligned}x^{4}&=x(3x^{2}+6x+2)\\&=3x^{3}+6x^{2}+2x\\&=3(3x^{2}+6x+2)+6x^{2}+2x\\&=x^{2}+6x+6.\end{aligned}}}$

Daher ist

${\displaystyle {}{\begin{aligned}(2x^{2}+5x+3)\cdot (3x^{2}+x+6)&=6x^{4}+3x^{3}+5x^{2}+5x+4\\&=6(x^{2}+6x+6)+3(3x^{2}+6x+2)+5x^{2}+5x+4\\&=6x^{2}+3x+4.\end{aligned}}}$

Berechne die Schnittpunkte der beiden Kreise ${\displaystyle {}K_{1}}$ und ${\displaystyle {}K_{2}}$, wobei ${\displaystyle {}K_{1}}$ den Mittelpunkt ${\displaystyle {}(3,4)}$ und den Radius ${\displaystyle {}6}$ und ${\displaystyle {}K_{2}}$ den Mittelpunkt ${\displaystyle {}(-8,1)}$ und den Radius ${\displaystyle {}7}$ besitzt.

Die Kreisgleichungen der beiden Kreise sind

${\displaystyle {}(x-3)^{2}+(y-4)^{2}=x^{2}-6x+y^{2}-8y+25=36\,}$

und

${\displaystyle {}(x+8)^{2}+(y-1)^{2}=x^{2}+16x+y^{2}-2y+65=49\,.}$

Die Differenz der beiden Gleichungen ergibt

${\displaystyle {}22x+6y+40=13\,.}$

Also ist

${\displaystyle {}y={\frac {-22x-27}{6}}\,.}$

Dies setzen wir in die erste Kreisgleichung ein und erhalten

${\displaystyle {}{\begin{aligned}x^{2}-6x+{\left({\frac {-22x-27}{6}}\right)}^{2}-8{\frac {-22x-27}{6}}-11&=x^{2}+{\frac {121}{9}}x^{2}-6x+33x+{\frac {81}{4}}+{\frac {88}{3}}x+36-11\\&={\frac {130}{9}}x^{2}+{\frac {169}{3}}x+{\frac {181}{4}}\\&=0.\end{aligned}}}$

Nach der Lösungsformel für eine quadratische Gleichung ist

${\displaystyle {}{\begin{aligned}x_{1,2}&={\frac {-{\frac {169}{3}}\pm {\sqrt {{\frac {28561}{9}}-4\cdot {\frac {130}{9}}\cdot {\frac {181}{4}}}}}{\frac {260}{9}}}\\&={\frac {-169\pm {\sqrt {28561-130\cdot 181}}}{\frac {260}{3}}}\\&={\frac {-3\cdot 169\pm 3{\sqrt {28561-23530}}}{260}}\\&={\frac {-507\pm 3{\sqrt {5031}}}{260}}\\&={\frac {-507\pm 9{\sqrt {559}}}{260}}.\end{aligned}}}$

Somit ist

${\displaystyle {}{\begin{aligned}y_{1}&={\frac {-22x_{1}-27}{6}}\\&={\frac {-22{\frac {-507+9{\sqrt {559}}}{260}}-27}{6}}\\&=-11{\frac {-169+3{\sqrt {559}}}{260}}-{\frac {9}{2}}\\&=-{\frac {33{\sqrt {559}}}{260}}+{\frac {11\cdot 13}{20}}-{\frac {9}{2}}\\&=-{\frac {33{\sqrt {559}}}{260}}+{\frac {53}{20}}\end{aligned}}}$

und

${\displaystyle {}{\begin{aligned}y_{2}&={\frac {-22x_{2}-27}{6}}\\&={\frac {-22{\frac {-507-9{\sqrt {559}}}{260}}-27}{6}}\\&=-11{\frac {-169-3{\sqrt {559}}}{260}}-{\frac {9}{2}}\\&={\frac {33{\sqrt {559}}}{260}}+{\frac {11\cdot 13}{20}}-{\frac {9}{2}}\\&={\frac {33{\sqrt {559}}}{260}}+{\frac {53}{20}}.\end{aligned}}}$

Die Schnittpunkte sind also

${\displaystyle \left({\frac {-507+9{\sqrt {559}}}{260}},\,-{\frac {33{\sqrt {559}}}{260}}+{\frac {53}{20}}\right)}$

und

${\displaystyle \left({\frac {-507-9{\sqrt {559}}}{260}},\,{\frac {33{\sqrt {559}}}{260}}+{\frac {53}{20}}\right).}$

Wir betrachten die durch die Gleichung

${\displaystyle {}X^{3}+Y^{3}=1\,}$

gegebene ebene algebraische Kurve.

1. Bestimme die Anzahl der Punkte dieser Kurve für den Körper ${\displaystyle {}\mathbb {Z} /(5)}$.
2. Bestimme die Anzahl der Punkte dieser Kurve für den Körper ${\displaystyle {}\mathbb {Z} /(7)}$.
3. Bestimme die Anzahl der Punkte dieser Kurve für den Körper ${\displaystyle {}\mathbb {Z} /(13)}$.
4. Bestimme die Anzahl der Punkte dieser Kurve für einen endlichen Körper ${\displaystyle {}{\mathbb {F} }_{q}}$ mit der Eigenschaft, dass ${\displaystyle {}q-1}$ und ${\displaystyle {}3}$ teilerfremd sind.

Wir schreiben die Gleichung als

${\displaystyle {}Y^{3}=1-X^{3}\,.}$

Dabei kann man sich für ${\displaystyle {}X}$ einen beliebigen Wert aus dem Körper vorgeben und muss sich fragen, ob und wie viele Lösungen es dann für ${\displaystyle {}Y}$ gibt. Da die Einheitengruppe eines endlichen Körpers zyklisch mit ${\displaystyle {}q-1}$ Elementen ist, ist das Potenzieren zum Exponenten ${\displaystyle {}3}$ bijektiv, wenn ${\displaystyle {}3}$ und ${\displaystyle {}q-1}$ teilerfremd sind, und hat einen Kern mit drei Elementen, falls ${\displaystyle {}3}$ und ${\displaystyle {}q-1}$ nicht teilerfremd sind. Im letzteren Fall gibt es ${\displaystyle {}{\frac {q-1}{3}}}$ Einheiten, die dritte Potenzen sind.

1. Siehe (4).
2. Es ist

   ${\displaystyle {}X}$	${\displaystyle {}0}$	${\displaystyle {}1}$	${\displaystyle {}2}$	${\displaystyle {}3}$	${\displaystyle {}4}$	${\displaystyle {}5}$	${\displaystyle {}6}$
   ${\displaystyle {}X^{3}}$	${\displaystyle {}0}$	${\displaystyle {}1}$	${\displaystyle {}1}$	${\displaystyle {}6}$	${\displaystyle {}1}$	${\displaystyle {}6}$	${\displaystyle {}6}$

   Somit gibt es bei ${\displaystyle {}X=0}$ drei Lösungen für ${\displaystyle {}Y^{3}=1-X^{3}}$, bei ${\displaystyle {}X=1,2,4}$ gibt es eine Lösung für ${\displaystyle {}Y^{3}=1-X^{3}}$ und bei ${\displaystyle {}X=3,5,6}$ gibt es keine Lösung für ${\displaystyle {}Y^{3}=1-X^{3}}$. Insgesamt gibt es also sechs Lösungen für diese Gleichung über ${\displaystyle {}\mathbb {Z} /(7)}$.

3. Bei ${\displaystyle {}\mathbb {Z} /(13)}$ gibt es nur vier Einheiten, die dritte Potenzen sind, da das Potenzieren zum Exponenten drei einen Kern mit drei Elementen besitzt. Diese vier dritten Potenzen sind (neben der ${\displaystyle {}0}$) gleich

   ${\displaystyle 1,\,8=2^{3},\,12=4^{3},\,5=8^{3}.}$

   Die einzige Möglichkeit, mit diesen Potenzen die Summe ${\displaystyle {}1}$ zu erhalten, ist ${\displaystyle {}0+1=1}$. Da ${\displaystyle {}1}$ drei dritte Einheitswurzeln besitzt, gibt es sechs Lösungen für diese Gleichung über ${\displaystyle {}\mathbb {Z} /(13)}$.

4. Nach Voraussetzung sind ${\displaystyle {}q-1}$ und ${\displaystyle {}3}$ teilerfremd, das bedeutet, dass das dritte Potenzieren bijektiv ist. Es gibt also zu jedem ${\displaystyle {}X\in {\mathbb {F} }_{q}}$ ein eindeutig bestimmtes ${\displaystyle {}Y}$, das die Gleichung ${\displaystyle {}Y^{3}=1-X^{3}}$ erfüllt. Somit gibt es in diesem Fall ${\displaystyle {}q}$ Lösungen.

Beweise den Satz über die Zerlegung einer affin-algebraischen Menge ${\displaystyle {}V\subseteq {{\mathbb {A} }_{K}^{n}}}$ in irreduzible Komponenten.

Die Existenz beweisen wir durch noethersche Induktion. Angenommen, nicht jede affin-algebraische Menge habe eine solche Zerlegung. Dann gibt es auch eine minimale Teilmenge, sagen wir ${\displaystyle {}V}$, ohne eine solche Zerlegung. ${\displaystyle {}V}$ kann nicht irreduzibel sein, sondern es gibt eine nicht-triviale Darstellung ${\displaystyle {}V=V_{1}\cup V_{2}}$. Da ${\displaystyle {}V_{1}}$ und ${\displaystyle {}V_{2}}$ echte Teilmengen von ${\displaystyle {}V}$ sind, gibt es für diese beiden jeweils endliche Darstellungen als Vereinigung von irreduziblen Teilmengen. Diese beiden vereinigen sich zu einer endlichen Darstellung von ${\displaystyle {}V}$, was ein Widerspruch ist.
Zur Eindeutigkeit. Seien

${\displaystyle {}V=V_{1}\cup \ldots \cup V_{k}=W_{1}\cup \ldots \cup W_{m}\,}$

zwei Zerlegungen in irreduzible Teilmengen (jeweils ohne Inklusionsbeziehung). Es ist

${\displaystyle {}V_{1}=V_{1}\cap V=V_{1}\cap (W_{1}\cup \ldots \cup W_{m})=(V_{1}\cap W_{1})\cup \ldots \cup (V_{1}\cap W_{m})\,.}$

Da ${\displaystyle {}V_{1}}$ irreduzibel ist, muss ${\displaystyle {}V_{1}\subseteq W_{j}}$ für ein ${\displaystyle {}j}$ sein. Umgekehrt ist mit dem gleichen Argument ${\displaystyle {}W_{j}\subseteq V_{i}}$ für ein ${\displaystyle {}i}$, woraus ${\displaystyle {}i=1}$ und ${\displaystyle {}V_{1}=W_{j}}$ folgt. Ebenso findet sich ${\displaystyle {}V_{2}}$ etc. in der Zerlegung rechts wieder, so dass die Zerlegung eindeutig ist.

Wir betrachten den Restklassenring

${\displaystyle {}R=K[U,V]/(U^{2}-U,V^{2}-V,U-2UV+V)\,}$

über einem Körper der Charakteristik ${\displaystyle {}\neq 2}$. Zeige ${\displaystyle {}U=V}$ in ${\displaystyle {}R}$.

Wir multiplizieren die Gleichung

${\displaystyle {}U+V-2UV=0\,}$

mit ${\displaystyle {}U}$ und erhalten

${\displaystyle {}0=U{\left(U+V-2UV\right)}=U^{2}+UV-2U^{2}V=U+UV-2UV=U-UV\,.}$

Durch Multiplikation mit ${\displaystyle {}V}$ erhält man entsprechend

${\displaystyle {}0=V-UV\,.}$

Also ist

${\displaystyle {}U=UV=V\,.}$

Es sei ${\displaystyle {}M}$ ein kommutatives Monoid, ${\displaystyle {}\Gamma }$ seine Differenzengruppe und ${\displaystyle {}K}$ ein Körper. Zeige, dass die Spektrumsabbildung

${\displaystyle K\!\!-\!\operatorname {Spek} \,{\left(\Gamma \right)}\longrightarrow K\!\!-\!\operatorname {Spek} \,{\left(M\right)}}$

injektiv ist.

Seien

${\displaystyle \varphi _{1},\varphi _{2}\colon \Gamma \longrightarrow K}$

Monoidhomomorphismen, also Elemente aus dem Spektrum zu ${\displaystyle {}\Gamma }$. Die Einschränkungen auf ${\displaystyle {}M}$, also die Verknüpfungen ${\displaystyle {}\varphi _{1}\circ i}$ und ${\displaystyle {}\varphi _{2}\circ i}$ mit ${\displaystyle {}i\colon M\rightarrow \Gamma }$, seien identisch. Es ist ${\displaystyle {}\varphi _{1}=\varphi _{2}}$ zu zeigen. Sei ${\displaystyle {}f-g\in \Gamma }$ mit ${\displaystyle {}f,g\in M}$. Da ${\displaystyle {}\Gamma }$ eine Gruppe ist, wird jedes Element auf eine Einheit in ${\displaystyle {}K}$ abgebildet. Also ist

${\displaystyle {}{\begin{aligned}\varphi _{1}(f-g)&=\varphi _{1}(f)\cdot \varphi _{1}(g)^{-1}\\&=\varphi _{2}(f)\cdot \varphi _{2}(g)^{-1}\\&=\varphi _{2}(f-g).\end{aligned}}}$

Beweise den Satz über die Charakterisierung von ganzen Elementen.

(1) ${\displaystyle {}\Rightarrow }$ (2). Wir betrachten die von den Potenzen von ${\displaystyle {}x}$ erzeugte ${\displaystyle {}R}$-Unteralgebra ${\displaystyle {}R[x]}$ von ${\displaystyle {}S}$, die aus allen polynomialen Ausdrücken in ${\displaystyle {}x}$ mit Koeffizienten aus ${\displaystyle {}R}$ besteht. Aus einer Ganzheitsgleichung

${\displaystyle {}x^{n}+r_{n-1}x^{n-1}+r_{n-2}x^{n-2}+\cdots +r_{1}x+r_{0}=0\,}$

ergibt sich

${\displaystyle {}x^{n}=-r_{n-1}x^{n-1}-r_{n-2}x^{n-2}-\cdots -r_{1}x-r_{0}\,.}$

Man kann also ${\displaystyle {}x^{n}}$ durch einen polynomialen Ausdruck von einem kleineren Grad ausdrücken. Durch Multiplikation dieser letzten Gleichung mit ${\displaystyle {}x^{i}}$ kann man jede Potenz von ${\displaystyle {}x}$ mit einem Exponenten ${\displaystyle {}\geq n}$ durch einen polynomialen Ausdruck von einem kleineren Grad ersetzen. Insgesamt kann man dann aber all diese Potenzen durch polynomiale Ausdrücke vom Grad ${\displaystyle {}\leq n-1}$ ersetzen. Damit ist

${\displaystyle {}R[x]=R+Rx+Rx^{2}+\cdots +Rx^{n-2}+Rx^{n-1}\,}$

und die Potenzen ${\displaystyle {}x^{0}=1,x^{1},x^{2},\ldots ,x^{n-1}}$ bilden ein endliches Erzeugendensystem von ${\displaystyle {}T=R[x]}$.

(2) ${\displaystyle {}\Rightarrow }$ (3). Sei ${\displaystyle {}x\in T\subseteq S}$, ${\displaystyle {}T}$ eine ${\displaystyle {}R}$-Unteralgebra, die als ${\displaystyle {}R}$-Modul endlich erzeugt sei. Dann ist ${\displaystyle {}xT\subseteq T}$, und ${\displaystyle {}T}$ enthält den Nichtnullteiler ${\displaystyle {}1}$.

(3) ${\displaystyle {}\Rightarrow }$ (1). Sei ${\displaystyle {}M\subseteq S}$ ein endlich erzeugter ${\displaystyle {}R}$-Untermodul mit ${\displaystyle {}xM\subseteq M}$. Seien ${\displaystyle {}y_{1},\ldots ,y_{n}}$ erzeugende Elemente von ${\displaystyle {}M}$. Dann ist insbesondere ${\displaystyle {}xy_{i}}$ für jedes ${\displaystyle {}i}$ eine ${\displaystyle {}R}$-Linearkombination der ${\displaystyle y_{j},\,j=1,\ldots ,n}$. Dies bedeutet

${\displaystyle {}xy_{i}=\sum _{j=1}^{n}r_{ij}y_{j}\,}$

mit ${\displaystyle {}r_{ij}\in R}$, oder, als Matrix geschrieben,

${\displaystyle {}x{\begin{pmatrix}y_{1}\\y_{2}\\\vdots \\y_{n}\end{pmatrix}}={\begin{pmatrix}r_{1,1}&r_{1,2}&\ldots &r_{1,n}\\r_{2,1}&r_{2,2}&\ldots &r_{2,n}\\\vdots &\vdots &\ddots &\vdots \\r_{n,1}&r_{n,2}&\ldots &r_{n,n}\end{pmatrix}}{\begin{pmatrix}y_{1}\\y_{2}\\\vdots \\y_{n}\end{pmatrix}}\,.}$

Dies schreiben wir als

${\displaystyle {}0={\begin{pmatrix}x-r_{1,1}&-r_{1,2}&\ldots &-r_{1,n}\\-r_{2,1}&x-r_{2,2}&\ldots &-r_{2,n}\\\vdots &\vdots &\ddots &\vdots \\-r_{n,1}&-r_{n,2}&\ldots &x-r_{n,n}\end{pmatrix}}{\begin{pmatrix}y_{1}\\y_{2}\\\vdots \\y_{n}\end{pmatrix}}\,.}$

Nennen wir diese Matrix ${\displaystyle {}A}$ (die Einträge sind aus ${\displaystyle {}S}$), und sei ${\displaystyle {}A^{\operatorname {adj} }}$ die adjungierte Matrix. Dann gilt ${\displaystyle {}A^{\operatorname {adj} }Ay=0}$ (${\displaystyle {}y}$ bezeichne den Vektor ${\displaystyle (y_{1},\ldots ,y_{n})}$) und nach der Cramerschen Regel ist ${\displaystyle {}A^{\operatorname {adj} }A=(\det A)E_{n}}$, also gilt ${\displaystyle {}((\det A)E_{n})y=0}$. Es ist also ${\displaystyle {}(\det A)y_{j}=0}$ für alle ${\displaystyle {}j}$ und damit

${\displaystyle {}(\det A)z=0\,}$

für alle ${\displaystyle {}z\in M}$. Da ${\displaystyle {}M}$ nach Voraussetzung einen Nichtnullteiler enthält, muss ${\displaystyle {}\det A=0}$ sein. Die Determinante ist aber ein normierter polynomialer Ausdruck in ${\displaystyle {}x}$ vom Grad ${\displaystyle {}n}$, so dass eine Ganzheitsgleichung vorliegt.

1. Skizziere die Nullstellengebilde

   ${\displaystyle {}V=V(XY,XZ,YZ)\subseteq {{\mathbb {A} }_{K}^{3}}\,}$

   und

   ${\displaystyle {}W=V(ST(S-T))\subseteq {\mathbb {A} }_{K}^{2}\,}$

   im reellen Fall.

2. Stifte einen bijektiven Morphismus

   ${\displaystyle \varphi \colon V\longrightarrow W.}$

3. Zeige, dass der Morphismus ${\displaystyle {}\varphi }$ außerhalb des Nullpunktes ein Isomorphismus ist (die Charakteristik des Körpers sei ${\displaystyle {}\neq 2}$).

1. 

   ${\displaystyle {}V=V(XY,XZ,YZ)=V(XY)\cup V(XZ)\cup V(YZ)\,}$

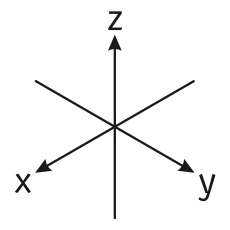
   ist die Vereinigung der drei Achsen im Raum.

2. Die lineare Abbildung

   ${\displaystyle K^{3}\longrightarrow K^{2},}$

   die durch die Matrix ${\displaystyle {}{\begin{pmatrix}1&0&1\\0&1&1\end{pmatrix}}}$ bezüglich der Standardbasen gegeben ist, bildet die ${\displaystyle {}X-Y}$-Ebene identisch auf sich ab und die ${\displaystyle {}Z}$-Achse auf die Hauptdiagonale in dieser Ebene. Damit liegt das Bild des Achsenkreuzes ganz im Nullstellengebilde ${\displaystyle {}W=V(ST(S-T))}$ und ergibt somit einen Morphismus ${\displaystyle {}\varphi \colon V\rightarrow W}$. Dieser ist bijektiv, da jede beteiligte Gerade bijektiv auf eine Gerade abgebildet wird.

3. Algebraisch liegt der ${\displaystyle {}K}$-Algebrahomomorphismus

   ${\displaystyle K[S,T]/(ST(S-T))\longrightarrow K[X,Y,Z]/(XY,XZ,YZ)}$

   mit ${\displaystyle {}S\mapsto X+Z}$ und ${\displaystyle {}T\mapsto Y+Z}$ vor. Dies induziert einen ${\displaystyle {}K}$-Algebrahomomorphismus der Nenneraufnahmen

   ${\displaystyle (K[S,T]/(ST(S-T)))_{S+T}\longrightarrow (K[X,Y,Z]/(XY,XZ,YZ))_{X+Y+2Z}.}$

   Dabei ist der Schnittpunkt von ${\displaystyle {}V(S+T)}$ bzw. ${\displaystyle {}V(X+Y+2Z)}$ mit den drei Geraden jeweils der Nullpunkt (die Charakteristik ist nicht ${\displaystyle {}2}$), so dass diese Nenneraufnahmen jeweils das Komplement des Nullpunktes beschreiben. Der rechte Ring ist, geschrieben in den Variablen ${\displaystyle {}A=X+Z,B=Y+Z,Z}$, gleich

   ${\displaystyle K[A,B,Z,(A+B)^{-1}]/((A-Z)Z,(B-Z)Z,(A-Z)(B-Z))).}$

   In diesem Ring ist Wegen

   ${\displaystyle {}2AB=2Z(A+B)-2Z^{2}=2Z(A+B)-AZ-BZ=Z(A+B)\,}$

   und somit ist

   ${\displaystyle {}Z={\frac {2AB}{A+B}}\,.}$

   Man kann also ${\displaystyle {}Z}$ eliminieren, die Idealerzeuger werden dann wegen

   ${\displaystyle {}A-Z=A-{\frac {2AB}{A+B}}={\frac {A^{2}+AB-2AB}{A+B}}={\frac {A^{2}-AB}{A+B}}\,}$

   zu

   ${\displaystyle {}{\begin{aligned}(A-Z)Z&={\frac {A^{2}-AB}{A+B}}\cdot {\frac {2AB}{A+B}}\\&={\frac {2A^{2}B(A-B)}{(A+B)^{2}}},\end{aligned}}}$

   ${\displaystyle {}{\begin{aligned}(B-Z)Z&={\frac {2AB^{2}(A-B)}{(A+B)^{2}}}\\\end{aligned}}}$

   und

   ${\displaystyle {}(A-Z)(B-Z)={\frac {A^{2}-AB}{A+B}}\cdot {\frac {B^{2}-AB}{A+B}}={\frac {A^{2}B^{2}+A^{2}B^{2}-AB^{3}-A^{3}B}{(A+B)^{2}}}\,.}$

   Da ${\displaystyle {}A+B}$ und ${\displaystyle {}2}$ Einheiten sind, bedeuten die beiden ersten Idealerzeuger

   ${\displaystyle {}A^{3}B=A^{2}B^{2}=AB^{3}\,,}$

   so dass der dritte Erzeuger überflüssig ist. Wegen

   ${\displaystyle {}AB(A-B)(A+B)=AB{\left(A^{2}-B^{2}\right)}\,}$

   gehört auch ${\displaystyle {}AB(A-B)}$ zum Ideal, das andererseits das Ideal erzeugt. Also ist die durch ${\displaystyle {}S\mapsto A}$ und ${\displaystyle {}T\mapsto B}$ gegebene Abbildung ein Isomorphismus.

Man gebe ein Beispiel einer integren, endlich erzeugten ${\displaystyle {}\mathbb {C} }$-Algebra ${\displaystyle {}R}$ und eines multiplikativen Systems ${\displaystyle {}S\subseteq R}$, ${\displaystyle {}0\not \in S}$, an derart, dass die Nenneraufnahme ${\displaystyle {}R_{S}}$ kein Körper ist, aber jedes maximale Ideal aus ${\displaystyle {}R}$ zum Einheitsideal in ${\displaystyle {}R_{S}}$ wird.

Sei ${\displaystyle {}R=\mathbb {C} [X,Y]}$ und ${\displaystyle {}S}$ das multiplikative System, das aus allen Produkten von Elementen der Form ${\displaystyle {}X-a,\,a\in \mathbb {C} }$, besteht. Die maximalen Ideale in ${\displaystyle {}R}$ haben die Form ${\displaystyle {}(X-a,Y-b)}$. Daher enthält jedes maximale Ideal ein Element aus ${\displaystyle {}S}$ und wird daher zum Einheitsideal in ${\displaystyle {}R_{S}}$. Das ist aber kein Körper, da genau die Primelemente ${\displaystyle {}X-a}$ zu Einheiten gemacht werden, alle anderen Primelemente (beispielsweise ${\displaystyle {}Y}$) aber nicht.

Beweise das Lemma von Nakayama.

Sei ${\displaystyle {}v_{1},\ldots ,v_{n}}$ ein Erzeugendensystem von ${\displaystyle {}V}$. Nach Voraussetzung gibt es wegen ${\displaystyle {}v_{i}\in {\mathfrak {m}}V}$ zu jedem ${\displaystyle {}v_{i}}$ eine Darstellung

${\displaystyle {}v_{i}=a_{i1}v_{1}+\cdots +a_{in}v_{n}\,}$

mit ${\displaystyle {}a_{ij}\in {\mathfrak {m}}}$. Daraus ergibt sich für jedes ${\displaystyle {}i}$ eine Darstellung

${\displaystyle {}(1-a_{ii})v_{i}=a_{i1}v_{1}+\cdots +a_{i,i-1}v_{i-1}+a_{i,i+1}v_{i+1}+a_{in}v_{n}\,.}$

Da ${\displaystyle {}a_{ii}\in {\mathfrak {m}}}$ ist, ist der Koeffizient ${\displaystyle {}1-a_{ii}}$ eine Einheit. Dies bedeutet aber, dass man nach ${\displaystyle {}v_{i}}$ auflösen kann, so dass also ${\displaystyle {}v_{i}}$ überflüssig ist. So kann man sukzessive auf alle Erzeuger verzichten, was bedeutet, dass der Nullmodul vorliegen muss.

Sei ${\displaystyle {}K}$ ein Körper. Zeige, dass sämtliche lokale Ringe der projektiven Geraden ${\displaystyle {}{\mathbb {P} }_{K}^{1}}$ isomorph zueinander sind. Man gebe eine möglichst einfache Beschreibung dieses Ringes.

Ein jeder Punkt ${\displaystyle {}P\in {\mathbb {P} }_{K}^{1}}$ liegt auf einer affinen Geraden ${\displaystyle {}P\in {\mathbb {A} }_{K}^{1}=D_{+}(L)\subset {\mathbb {P} }_{K}^{1}}$. Dabei bezeichnet ${\displaystyle {}L}$ eine homogene Linearform. Weiter kann man durch Verschieben auf der affinen Geraden annehmen, dass es sich um den Nullpunkt handelt. Da man dies für jeden Punkt machen kann und da dies den lokalen Ring nicht ändert, sind alle lokalen Ringe isomorph untereinander. Der Nullpunkt auf der affinen Geraden besitzt als lokalen Ring die Lokalisierung ${\displaystyle {}K[X]_{(X)}}$.

Bestimme den Durchschnitt

${\displaystyle V_{+}(X)\cap V_{+}(Y)}$

in ${\displaystyle {}{\mathbb {P} }_{K}^{2}}$.

Für einen Punkt

${\displaystyle {}P=(a,b,c)\in V_{+}(X)\cap V_{+}(Y)\,}$

muss die erste und die zweite Koordinate gleich ${\displaystyle {}0}$ sein, der einzige Punkt auf den beiden Geraden ist demnach in homogenen Geraden gleich ${\displaystyle {}(0,0,1)}$.