- Übungsaufgaben
Die folgende Aufgabe löse man direkt ohne Ableitungsregeln und durch Induktion mit Hilfe der Produktregel.
Aufgabe
Aufgabe
Aufgabe
Aufgabe
Aufgabe *
Bestimme direkt (ohne Verwendung von Ableitungsregeln) die Ableitung der Funktion
in einem beliebigen Punkt .
Aufgabe *
Wir betrachten die Funktion
Bestimme die Tangenten an , die lineare Funktionen sind (die also durch den Nullpunkt verlaufen).
Aufgabe
Aufgabe *
Beweise die Produktregel für differenzierbare Funktionen unter Verwendung der Regel
mit Hilfe von
Aufgabe
Aufgabe
Zeige, dass die Ableitung einer rationalen Funktion wieder eine rationale Funktion ist.
Aufgabe
Es sei und . Bestimme die Ableitung der Hintereinanderschaltung direkt und mittels der Kettenregel.
Aufgabe *
Es sei und .
a) Bestimme die Ableitung von und von .
b) Berechne die Hintereinanderschaltung .
c) Bestimme die Ableitung von mit Hilfe von Teil b).
d) Bestimme die Ableitung von mittels der Kettenregel.
Aufgabe
Es sei und . Bestimme die Ableitung der Hintereinanderschaltung direkt und mittels der Kettenregel.
Aufgabe
Zeige, dass ein Polynom genau dann einen Grad besitzt (oder ist), wenn die -te Ableitung von das Nullpolynom ist.
Aufgabe *
Es seien
zwei differenzierbare Funktionen und sei
a) Drücke die Ableitung mit den Ableitungen von und aus.
b) Sei nun
Berechne auf zwei verschiedene Arten, einerseits über und andererseits über die Formel aus Teil .
Aufgabe *
Es sei
eine differenzierbare Funktion. Zeige durch Induktion, dass für die -fache Hintereinanderschaltung ()
die Beziehung
gilt.
Aufgabe
Aufgabe
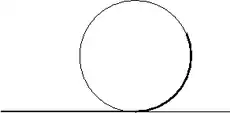
Die Funktion
sei für negatives konstant gleich und folge für dem unteren rechten Viertelkreis mit Mittelpunkt und Radius . Bestimme den Grad der Differenzierbarkeit dieser Funktion.
Aufgabe *
Aufgabe
Es sei
ein Polynom vom Grad und die Tangente an im Punkt . Zeige die Beziehung
mit einem Polynom vom Grad .
Aufgabe *
Es sei
ein Polynom vom Grad , ein Punkt und die Tangente an im Punkt . Zeige die Beziehung
mit einem Polynom vom Grad .
- Aufgaben zum Abgeben
Aufgabe (3 Punkte)
Bestimme die Ableitung der Funktion
wobei die Menge sei, auf der das Nennerpolynom nicht verschwindet.
Aufgabe (4 Punkte)
Aufgabe (3 Punkte)
Aufgabe (4 Punkte)
Es sei ein Polynom, und . Zeige, dass genau dann ein Vielfaches von ist, wenn eine Nullstelle sämtlicher Ableitungen ist.
Aufgabe (4 Punkte)
Es sei
eine rationale Funktion. Zeige, dass genau dann ein Polynom ist, wenn es eine (höhere) Ableitung mit gibt.
| << | Kurs:Analysis (Osnabrück 2014-2016)/Teil I | >> |
|---|