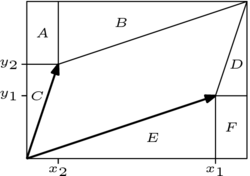
Man begründe anhand des Bildes, dass zu zwei Vektoren ${\displaystyle {}(x_{1},y_{1})}$ und ${\displaystyle {}(x_{2},y_{2})}$ die Determinante der durch die Vektoren definierten ${\displaystyle {}2\times 2}$-Matrix mit dem Flächeninhalt des von den beiden Vektoren aufgespannten Parallelogramms (bis auf das Vorzeichen) übereinstimmt.

${\displaystyle {}\,}$

Es seien ${\displaystyle {}P_{1}=(a_{1},b_{1}),\,P_{2}=(a_{2},b_{2})}$ und ${\displaystyle {}P_{3}=(a_{3},b_{3})}$ drei Punkte im ${\displaystyle {}\mathbb {R} ^{2}}$. Stelle den Flächeninhalt des zugehörigen Dreiecks mit ${\displaystyle {}a_{1},b_{1},a_{2},b_{2},a_{3},b_{3}}$ dar.

Drücke die Funktion ${\displaystyle {}\nu ^{2}}$ als Funktion der ${\displaystyle {}L_{ij}^{2}}$ (siehe Vorlesung 1) aus.

Drücke die Funktion ${\displaystyle {}S_{12}+S_{13}+S_{23}}$ als Funktion der ${\displaystyle {}L_{ij}^{2}}$ (siehe Vorlesung 1) aus.

Wir betrachten die Abbildung

${\displaystyle \mathbb {R} ^{6}\longrightarrow \mathbb {R} ^{3},\,\left(x_{1},\,y_{1},\,x_{2},\,y_{2},\,x_{2},\,y_{2}\right)\longmapsto \left({\sqrt {{\left(x_{1}-x_{2}\right)}^{2}+{\left(y_{1}-y_{2}\right)}^{2}}},\,{\sqrt {{\left(x_{1}-x_{3}\right)}^{2}+{\left(y_{1}-y_{3}\right)}^{2}}},\,{\sqrt {{\left(x_{2}-x_{3}\right)}^{2}+{\left(y_{2}-y_{3}\right)}^{2}}}\right),}$

die einem Dreieck die Längen seiner Seiten zuordnet. Zeige, dass das Bild dieser Abbildung die Punkte ${\displaystyle {}\left(\ell _{1},\,\ell _{2},\,\ell _{3}\right)\in \mathbb {R} _{\geq 0}^{3}}$ sind, die die Dreiecksungleichung erfüllen.

Diskutiere die Ähnlichkeit von Dreiecken analog zu Beispiel 1.1.

Wir fassen ein Dreieck ${\displaystyle {}\triangle }$ als ein geordnetes Tripel ${\displaystyle {}(P_{1},P_{2},P_{3})\in \mathbb {R} ^{6}}$ auf. Begründe die folgenden topologischen Eigenschaften.

1. Die Menge der nichtentarteten Dreiecke ist offen.
2. Die Menge der gleichseitigen Dreiecke ist abgeschlossen.
3. Die Menge der gleichschenkligen Dreiecke ist abgeschlossen.

Wir betrachten die Abbildung

${\displaystyle \mathbb {R} ^{6}\longrightarrow \mathbb {R} ^{3},\,\left(x_{1},\,y_{1},\,x_{2},\,y_{2},\,x_{2},\,y_{2}\right)\longmapsto \left({\left(x_{1}-x_{2}\right)}^{2}+{\left(y_{1}-y_{2}\right)}^{2},\,{\left(x_{1}-x_{3}\right)}^{2}+{\left(y_{1}-y_{3}\right)}^{2},\,{\left(x_{2}-x_{3}\right)}^{2}+{\left(y_{2}-y_{3}\right)}^{2}\right),}$

die einem Dreieck die Längenquadrate seiner Seiten zuordnet. Bestimme die regulären Punkte der Abbildung.

Es sei ${\displaystyle {}K}$ ein Körper und sei ${\displaystyle {}R=K[X_{1},\ldots ,X_{n}]}$ der Polynomring über ${\displaystyle {}K}$. Zeige, dass ein Polynom ${\displaystyle {}F\in R}$ genau dann symmetrisch ist, wenn die homogenen Komponenten von ${\displaystyle {}F}$ symmetrisch sind.

Es sei ${\displaystyle {}K}$ ein Körper und sei ${\displaystyle {}R=K[X_{1},\ldots ,X_{n}]}$ der Polynomring über ${\displaystyle {}K}$. Zu ${\displaystyle {}f\in R}$, ${\displaystyle {}f\neq 0}$, sei ${\displaystyle {}\operatorname {LM} _{}^{}{\left(f\right)}}$ das Leitmonom zu ${\displaystyle {}f}$ in der gradlexikographischen Ordnung. Zeige, dass das Leitmonom sich multiplikativ verhält, dass also

${\displaystyle {}\operatorname {LM} _{}^{}{\left(fg\right)}=\operatorname {LM} _{}^{}{\left(f\right)}\cdot \operatorname {LM} _{}^{}{\left(g\right)}\,}$

für Polynome ${\displaystyle {}f,g\neq 0}$ gilt.

Schreibe das symmetrische Polynom

${\displaystyle X^{3}Y^{3}-2X^{2}-2Y^{2}+5XY}$

als Polynom in den elementarsymmetrischen Polynomen.

Schreibe das symmetrische Polynom

${\displaystyle 3X^{2}Y^{2}Z^{2}-X^{4}-Y^{4}-Z^{4}+X^{3}Y^{3}Z^{3}}$

als Polynom in den elementarsymmetrischen Polynomen.

Schreibe die symmetrischen Polynome

${\displaystyle X_{1}^{k}+\cdots +X_{n}^{k}}$

als Polynom in den elementarsymmetrischen Polynomen.

Bestimme die Fasern (bis auf Homöomorphie) der Längenabbildung ${\displaystyle {}L}$ aus Beispiel 1.1.

Wir betrachten die Abbildung

${\displaystyle L\colon \mathbb {R} ^{6}\longrightarrow \mathbb {R} ^{3},\,\left(x_{1},\,y_{1},\,x_{2},\,y_{2},\,x_{2},\,y_{2}\right)\longmapsto \left({\sqrt {{\left(x_{1}-x_{2}\right)}^{2}+{\left(y_{1}-y_{2}\right)}^{2}}},\,{\sqrt {{\left(x_{1}-x_{3}\right)}^{2}+{\left(y_{1}-y_{3}\right)}^{2}}},\,{\sqrt {{\left(x_{2}-x_{3}\right)}^{2}+{\left(y_{2}-y_{3}\right)}^{2}}}\right),}$

die einem Dreieck die Längen seiner Seiten zuordnet. Es sei ${\displaystyle {}B}$ das Bild der Abbildung. Gibt es eine stetige Abbildung

${\displaystyle s\colon B\longrightarrow \mathbb {R} ^{6}}$

${\displaystyle {}L\circ s=\operatorname {Id} _{B}\,?}$

Es sei ${\displaystyle {}K}$ ein algebraisch abgeschlossener Körper. Zeige, dass die Abbildung

${\displaystyle K^{6}\longrightarrow K^{3},\,\left(x_{1},\,y_{1},\,x_{2},\,y_{2},\,x_{2},\,y_{2}\right)\longmapsto \left({\left(x_{1}-x_{2}\right)}^{2}+{\left(y_{1}-y_{2}\right)}^{2},\,{\left(x_{1}-x_{3}\right)}^{2}+{\left(y_{1}-y_{3}\right)}^{2},\,{\left(x_{2}-x_{3}\right)}^{2}+{\left(y_{2}-y_{3}\right)}^{2}\right),}$

surjektiv ist.

Es sei ${\displaystyle {}K}$ ein Körper, der eine dritte primitive Einheitswurzel ${\displaystyle {}\zeta }$ enthalte. Zeige, dass das Polynom

${\displaystyle {\left(X_{1}+\zeta X_{2}+\zeta ^{2}X_{3}\right)}^{3}\in K[X_{1},X_{2},X_{3}]}$

symmetrisch ist und bestimme seine Darstellung mit den elementarsymmetrischen Polynomen.

Bestimme die kritischen Punkte der durch die elementarsymmetrischen Polynome definierten Gesamtabbildung

${\displaystyle \mathbb {R} ^{n}\longrightarrow \mathbb {R} ^{n},\,{\left(x_{1},\ldots ,x_{n}\right)}\longmapsto {\left(E_{1}{\left(x_{1},\ldots ,x_{n}\right)},\ldots ,E_{n}{\left(x_{1},\ldots ,x_{n}\right)}\right)}.}$