| Aufgabe | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Punkte | 3 | 3 | 4 | 2 | 4 | 4 | 3 | 3 | 3 | 2 | 3 | 4 | 2 | 3 | 1 | 5 | 5 | 2 | 2 | 4 | 2 | 64 |
Aufgabe * (3 Punkte)
Definiere die folgenden (kursiv gedruckten) Begriffe.
- Eine Gerade in Punktvektorform im .
- Die
beschreibende Matrix
zu einer
linearen Abbildung
bezüglich der Standardbasen.
- Eine Äquivalenzrelation auf einer Menge .
- Ein Dedekindscher Schnitt.
- Der trigonometrische Punkt zu einem Winkel .
- Ein endlicher Wahrscheinlichkeitsraum.
Aufgabe * (3 Punkte)
Formuliere die folgenden Sätze.
- Der Satz über den Lösungsraum bei einer linearen Gleichung.
- Der Satz über die Eindeutigkeit des Limes in einem angeordneten Körper .
- Der Satz über Nullstellen und lineare Faktoren eines Polynoms .
Aufgabe * (4 (2+2) Punkte)
Ein lineares Ungleichungssystem sei durch die Ungleichungen
gegeben.
a) Skizziere die Lösungsmenge dieses Ungleichungssystems.
b) Bestimme die Eckpunkte der Lösungsmenge.
Aufgabe * (2 Punkte)
Bestimme die Punktrichtungsform für die durch die Gleichung
im gegebene Gerade.
Aufgabe * (4 Punkte)
Beweise das Injektivitätskriterium für eine lineare Abbildung
Aufgabe * (4 Punkte)
Es seien rationale Zahlen. Zeige, dass
genau dann gilt, wenn es ein mit gibt.
Aufgabe * (3 Punkte)
Bestimme das inverse Element zu in .
Aufgabe * (3 Punkte)
Es sei ein Körper. Wir betrachten die Abbildung
Welche Eigenschaften eines Ringhomomorphismus erfüllt die Abbildung , welche nicht?
Aufgabe * (3 Punkte)
Aufgabe * (2 Punkte)
Berechne
Aufgabe * (3 Punkte)
Aufgabe * (4 Punkte)
Beweise den Satz, dass der Limes einer konvergenten Folge in einem angeordneten Körper eindeutig bestimmt ist.
Aufgabe * (2 Punkte)
Es sei eine nichtnegative reelle Zahl. Für jedes , gelte . Zeige .
Aufgabe * (3 Punkte)
Aufgabe (1 Punkt)
Erläutere die geometrische Relevanz des geometrischen Mittels.
Aufgabe * (5 Punkte)
Beweise die Lösungsformel für quadratische Gleichungen.
Aufgabe * (5 Punkte)
Es sei
ein normiertes Polynom über einem Körper . Es seien drei (verschiedene) Zahlen aus . Zeige, dass diese drei Zahlen genau dann Nullstellen von sind, wenn sie das Gleichungssystem
erfüllen.
Aufgabe * (2 Punkte)
Fridolin sagt:
„Irgendwas kann am Zwischenwertsatz nicht stimmen. Für die stetige Funktion
gilt und . Nach dem Zwischenwertsatz müsste es also eine Nullstelle zwischen und geben, also eine Zahl mit . Es ist doch aber stets .“
Wo liegt der Fehler in dieser Argumentation?
Aufgabe * (2 Punkte)
Ordne die folgenden Funktionen den Bildern zu (man schreibe ohne Begründung hinter den Funktionsausdruck den Buchstaben des zugehörigen Bildes; nur für vollständig richtige Antworten gibt es Punkte).
 a)
a) b)
b)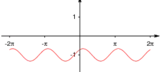 c)
c)
 d)
d) e)
e) f)
f)
Aufgabe * (4 Punkte)
Bestimme die Wahrscheinlichkeit, dass man beim Zahlenlotto (genau) drei Richtige hat.
Aufgabe * (2 Punkte)
Wir betrachten den Wahrscheinlichkeitsraum mit der Laplace-Dichte. Es sei das Ereignis, dass eine Zahl aus ein Vielfaches der ist, und das Ereignis, dass eine Zahl aus ein Vielfaches der ist. Sind und unabhängig?