- Ebene monomiale Kurven und Knoten
In den letzten beiden Vorlesungen haben wir (hauptsächlich im Zweidimensionalen) gezeigt, inwiefern sich eine isolierte Singularitäten in der lokalen Fundamentalgruppe niederschlägt. Die lokale Fundamentalgruppe ist eine intrinsische topologische Invariante der affin-algebraischen Menge und unabhängig von der Einbettung von in einen . In dieser Vorlesung werden wir eine Beispielklasse anschauen, bei der die Singularität keine Auswirkung auf die intrinsische topologische Gestalt von hat, bei der aber die Singularität eine starke topologische Auswirkung auf Invarianten der Einbettung besitzt.
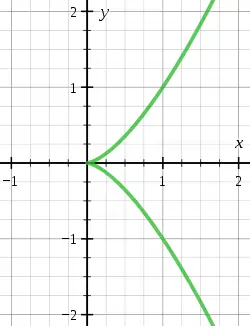
Wir betrachten die Nullstellenmenge
die bei eine isolierte Singularität im Nullpunkt besitzt. Wenn und teilerfremd sind, so ist das Polynom
irreduzibel und damit ist auch irreduzibel. Diese Eigenschaft werden wir im Folgenden voraussetzen, das einfachste singuläre Beispiel ist die Neilsche Parabel. Eine andere wichtige Beschreibung von ergibt sich als Bild der polynomialen Abbildung
Jeder Bildpunkt erfüllt offenbar die beschreibende Gleichung. Bei vorausgesetzter Teilerfremdheit der Exponenten kann man einfach zeigen, dass die Abbildung sogar bijektiv ist. Es gibt also eine polynomiale Bijektion , wobei glatt und singulär ist. Von daher könnte man meinen, dass die Singularität von topologisch keine besondere Relevanz haben sollte. In der Tat liegt ein Homöomorphismus zwischen und vor. Wir werden aber zeigen, dass die Singularität sehr wohl eine topologische Relevanz besitzt, und zwar in der Art, wie sie im umgebenden Raum
eingebettet ist. Ein erster wichtiger Hinweis in diese Richtung ergibt sich, wenn man die Abbildung mit der Standarddurchlauf des Einheitskreises verknüpft. Dieser ist durch
gegeben. Verknüpft mit erhält man die Abbildung
Da eine Homöomorphie vorliegt, ist dieser Weg ein Erzeuger der Fundamentalgruppe von , ebenso wie der Standarddurchlauf des Einheitskreises ein Erzeuger der Fundamentalgruppe von ist. Ein Unterschied besteht aber in der Verschlingung dieses Weges im .
Wir Identifizieren den mit dem und schreiben und . Im arbeiten wir also mit den reellen Koordinaten . Eine komplexe Zahl ist genau dann , wenn sowohl ihr Realteil als auch ihr Imaginäreteil ist. Die definierende Gleichung
für ein komplexes Zahlenpaar bedeutet daher ins Reelle übersetzt, wegen
(und entsprechend für ), dass die beiden reellen Geichungen
und
simultan erfüllt sein müsssen. Für die Neilsche Parabel bedeutet das, dass die beiden Gleichungen
und
erfüllt sein müssen.
Auf wirkt die multiplikative Gruppe durch die Operation
Diese Gruppenwirkung hängt mit der -Graduierung des Restklassenringes durch und zusammen. Wir schränken die Operation auf positive reelle Zahlen ein. Diese Operation setzt sich auf dem gesamten fort, durch
Die Bahnen dieser Operation zu einem Punkt sind selbst wieder reelle mit Koeffizienten versehene monomiale Kurven im Vierdimensionalen. Für streben diese Bahnen gegen den Nullpunkt und für gegen Unendlich. Diese Bahnen sollte man in Analogie zu den Strahlen (Halbgeraden) im sehen, die vom Nullpunkt ausgehen. Jedes Strahl durchstößt die Sphäre in genau einem Punkt. Eine entsprechende Aussage gilt auch für die gegenwärtigen Bahnen.
Es sei
die reell dreidimensionale Sphäre im reell vierdimensionalen Raum. Wir betrachten den Durchschnitt
Da reell zweidimensional ist, erwartet man (reelle Kodimensionen zählen) einen reell eindimensionalen Schnitt. steht hier für Link, auf Deutsch Umgebungsrand. Es ist generell ein wichtiges topologisches Hilfsmittel, zu einer affin-algebraischen Varietät
mit einer Singularität im Nullpunkt den Durchschnitt mit der reell -dimensionalen Sphäre zu betrachten, also . Dabei ist für geeignete Sphärenradien der Durchschnitt eine reelle Mannigfaltigkeit, deren Dimension um kleiner als die reelle Dimension von ist.
In unserer Situation liegt insgesamt das kommutative Diagramm
von Homöomorphismen vor. Dabei steht oben die Polarkoordinantenabbildung, rechts steht mit der Umkehrabbildung , wobei gelte (siehe Lemma 5.3), und unten , was wir gleich als bijektiv nachweisen werden.
Lemma
Es sei
mit teilerfremd. Es sei .
Dann ist die Abbildung
eine Homöomorphie. Die Verknüpfung von
mit und der Projektion auf ergibt eine Homöomorphie zwischen und .
Beweis
Die Abbildung ist wohldefiniert und stetig. Zu einem fixierten, von verschiedenen Punkt
zeigen wir, dass es ein eindeutiges Urbild gibt. Wir behaupten, dass die reelle Bahn , durch diesen Punkt die dreidimensionale Sphäre in genau einem Punkten schneidet. Die Schnittbedingung ist
Wegen der monomialen Bedingung sind sowohl als auch von verschieden und daher sind und positive reelle Zahlen. Es liegt also eine Gleichung der Form
vor. Die Gleichung
beschreibt eine Ellipse und es muss wegen der Positivität von
und
gelten. Dafür gibt es nur eine Lösung in . (dies sieht man auch, wenn man nach ableitet und das aymptotische Verhalten dieser Funktion betrachtet). Das legt über etc. auch die anderen Koordinaten im Urbild fest.
Die Norm von ist wegen
gleich . Es sei die eindeutig bestimmte positive reelle Zahl mit
Die beschriebene Hintereinanderschaltung ist dann
Wir betrachten nun das Paar bestehend aus der Sphäre und , das homöomorph zu ist.
Wenn man aus einen Punkt herausnimmt, der nicht auf dem eingebetteten liegt, so erhält man eine -Sphäre im . Ein solches Gebilde nennt man einen Knoten.
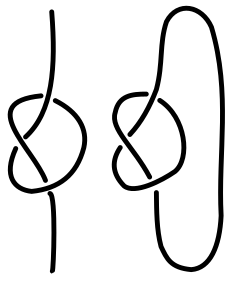
Definition
Unter einem Knoten versteht man eine topologische Einbettung der -Sphäre in den Raum
Manchmal beschränkt man sich auf stetig differenzierbar eingebettete Kreise.
Definition
Zwei Knoten und heißen äquivalent, wenn es eine stetige Abbildung
derart gibt, dass für jedes die Abbildung ein Homöomorphismus des ist, dass die Identität ist und dass
ist.
Die Bildknoten beschreiben dabei eine stetige Deformation des ersten Knoten in den zweiten Knoten mit dem Zeitparameter .

Streng genommen meint man die Standardeinbettung dieses Knotens, also di Abbildung
doch ist jeder andere Durchlauf dazu äquivalent.
Zur Orientierung der im Folgenden zu besprechenden Knoten ist der Begriff des Torus und des Torusknotens hilfreich.
Definition
Die Produktmannigfaltigkeit heißt Torus.
Der Torus ist in natürlicher Weise eine abgeschlossene zweidimensionale Untermannigfaltigkeit des . Ein Torus lässt sich aber auch einfach als abgeschlossene Untermannigfaltigkeit des realisieren, beispielsweise, indem man einen Kreis um eine Gerade außerhalb des Kreises rotieren lässt. Ein Torus ist somit einfach ein Fahrradschlauch.

Wir arbeiten nun mit Polarkoordinaten für die beiden , und zwar sei
und
Auf sind beiden Koordinaten nicht , und daher kann man mit diesen Koordinaten alles erfassen. In diesen Koordinaten ist
In der Polarkoordinatenbeschreibung wird durch
beschrieben. Dabei ist die zweite Gleichung als Winkelgleichung, also modulo zu verstehen. In dieser Darstellung erkennt man den positiven Quadranten der reellen monomialen Kurve, wenn man die Winkelgleichung vergisst. Die Lösungsmenge der Winkelgleichung, also
ist innerhalb von der „Funktionsgraph“ zu
der allerdings aus verschiedenen parallelen Strecken besteht. Sie ist homöomorph zum .
Wenn man auch auf der Normalisierung der Kurve Polarkoordinaten einführt, so ist die Normalisierungsabbildung durch
gegeben.
Der erzeugende Weg der Fundamentalgruppe von hat in beiden komplexen Koordinaten den Radius und ist daher ein Weg auf dem Torus . Er dreht sich um den ersten Kreis -fach und um den zweiten -fach. Um einen Weg auf dem Link zu erreichen, muss man den Weg
mit wie im Beweis zu Lemma 11.1 nehmen. Dies ändert nichts daran, dass der Weg auf einem Torus verläuft (wobei die beiden Kreise jetzt untershciedliche Radien haben) und wie oft sich der Weg in den beiden Richtungen dreht.
Wenn man den ohne einen Punkt auf den homöomorph abbildet (etwa durch die stereographische Projektion,) und der Projektionspunkt nicht auf diesem Torus und damit auch nicht auf liegt, so wird der Torus homöomorph auf einen Torus im abgebildet. Daraus ist ersichtlich, dass es sich bei um einen Torusknoten handelt. Bei und ist dieser Knoten die sogenannte Kleeblattschlinge.

Bei oder ergibt sich ein Torusknoten, der einmal längs des einen Kreises und beliebig oft längs des anderen Kreises läuft. Das ist dann aber ein trivialer Knoten, man denke an die homöomorphe Projektion dieses Knoten auf die Ebene, die einen geschlängelten Kreis ergibt. Wir halten die folgende topologische Auswirkung einer Singularität fest: Die ebene monomiale Kurve ist genau dann regulär, wenn der zu ihr gehörende Link trivial ist.
Wir behandeln abschließend noch den Fall, wo die Exponenten der Variablen nicht teilerfremd sind. Der Link besteht dann aus mehreren eindimensionalen Sphären, die im in einer bestimmten charakteristischen Weise miteinander verschlungen sind.
Lemma
Es sei
mit teilerfremd.
Dann gibt es eine Faktorzerlegung
wobei eine -te primitive Einheitswurzel ist. Die Komponenten sind untereinander isomorph und schneiden sich paarweise im Nullpunkt.
Beweis
Es gilt
Wenn man und einsetzt, so erhält man das Resultat. Es sei eine -te Wurzel von . Dann ist
ein Isomorphismus. Ferner ist bei
die Nullstellenmenge davon ist allein der Nullpunkt.
Dies bedeutet insbesondere, dass der Durchschnitt aus disjunkten bestehen.
Beispiel

Wir betrachen die monomiale Gleichung
in , wo also die beiden Exponenten nicht teilerfremd sind. Diese Kurve kann auch durch die Gleichung beschrieben werden, es handelt sich also um das komplexe Achsenkreuz . In diesem Fall besteht der Durchschnitt
aus zwei disjunkten Kreisen. Diese beiden Kreise sind einfach ineinander verschlungen. Man spricht von der Hopfverschlingung.
Beispiel
Wir betrachen die monomiale Gleichung
in ,die beiden Exponenten sind also nicht teilerfremd sind. Das beschreibende Polynome zerfällt , die Nullstellenmenge ist also die Vereinigung von zwei Parablen. Der Durchschnitt besteht allein aus dem Nullpunkt. Daher besteht
aus zwei disjunkten Kreisen. Diese beiden Kreise sind doppelt ineinander verschlungen.
| << | Kurs:Singularitätentheorie (Osnabrück 2019) | >> |
|---|