Steigung und y Achsenabschnitt

Lineare Funktion Alltagsbeispiel

1. 1. 
   2. ${\displaystyle H(a)\approx 205{,}63\ a+346\ }$
      (H in m und a in km)
   3. ${\displaystyle ca.\ 446{,}76\ m}$
   4. ${\displaystyle ca.\ 1041\ m}$
2. 1. 
   2. ${\displaystyle T(a)=-0{,}012\ a-1{,}4\ }$
      (T und a in m)
   3. ${\displaystyle 1{,}7\ m}$
   4. ${\displaystyle 16{,}{\dot {6}}\ m}$
3. 1. 
   2. ${\displaystyle M(e)=0{,}00405\ e+0{,}8\ }$
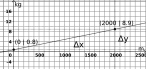
      (M in kg und e in €)
   3. ${\displaystyle 1134{,}8\ kg}$
   4. ${\displaystyle 740{,}{\overline {740}}\ {\text{€}}}$
4. 1. 
      
   
   
   2. ${\displaystyle F(k)=-0{,}004\ k+4\ }$
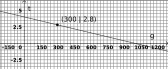
      (F in t CO₂ und k in g Obstkonsum)
   3. ${\displaystyle 0{,}48\ t}$
   4. ${\displaystyle 1000\ g}$

Tabelle für eine lineare Funktion erstellen

Diagramm einer linearen Funktion mit Hilfe von zwei Punkten erstellen

Eine lineare Funktion mit Hilfe von zwei Punkten ermitteln

1. ${\displaystyle \ y={\frac {5x-5}{4}}}$
   x: Tonnen, y: 1000 €, S: 1000 €/t
2. ${\displaystyle \ y=-0{,}5x+70}$
   x: cm, y: Hz, S: Hz/cm
3. ${\displaystyle \ y=-0{,}4x+100}$
   x: °C, y: g/L, S: g/(L mal °C).
4. ${\displaystyle \ y=-{\frac {17x}{30}}+85}$
   x: Zig./Tag, y: Jahre, S: Jahre mal Tag/Zig.
5. ${\displaystyle \ y=205{,}63x+346}$
   x: km, y: m, S: m/km
6. ${\displaystyle \ y=-0{,}004x+4}$
   x: g Obst, y: t CO₂, S: g/t
7. ${\displaystyle \ y=-3x+5{,}25}$
   x: h, y: m, S: m/h
8. ${\displaystyle \ y=-{\frac {17x}{30}}+85}$
   x: Zig./Tag, y: Jahre, S: Jahre mal Tag/Zig.

Mittlere Änderungsrate

1. 1. 0,5°C
   2. 0°C/h
   3. 0,06°C/h. Die Temperatur ist durchschnittlich um 0,06°C pro Stunde gestiegen
2. 1. 40 Prozenteinheiten
   2. 2,5% pro Minute (Abnahme)
   3. 2,5% pro Minute. Jede Minute werden durchschnittlich 2,5% des Schmutzes abgebaut
3. 1. ca. 3,5°C
   2. ca. 0,67°C/m
   3. 0°C/m. Die Temperatur ist durchschnittlich gleich geblieben
4. 1. 500000 Menschen
   2. 50000 Menschen pro Jahr
   3. ca. 166667 Menschen pro Jahr. Die Bevölkerung ist für dieses Intervall durchschnittlich um 166667 Menschen pro Jahr gewachsen.

Einheiten der Steigung

Die Steigung und ihre Zusammenhänge

1. hier klicken (Video)
2. hier klicken (Video)
3. hier klicken (Video)

Textaufgaben zu den linearen Funktionen

1. 1. ${\displaystyle V(t)=-0{,}05\ t+46\ }$ (t in min V in Liter)
   2. ${\displaystyle 920\ min}$
   3. ${\displaystyle 420\ min}$
2. 1. ${\displaystyle h(t)=3{,}5\ t+0{,}5\ }$ (t in min h in km)
   2. ${\displaystyle ca.\ 1{,}96\ km}$
   3. ${\displaystyle 60\ s\ (1\ min)}$
3. 1. ${\displaystyle H(t)=-1{,}4\ t+18\ }$ (t in h, H in cm)
   2. ${\displaystyle ca.\ 771{,}4\ min}$
   3. ${\displaystyle ca\ 18{,}0\ cm\ (17{,}9615\ cm)}$
4. 1. ${\displaystyle s(t)=-72\ t+311\ }$ (t in h, s in km)
      (Abstand von Brüssels aus)
   2. ${\displaystyle 4\,h\,19\,min\,10\,s}$
   3. ${\displaystyle 282{,}2\ km\ und\ 28{,}8\ \ }$
      (von Brüssels bzw. von Paris)
   4. ${\displaystyle 5{,}04\approx 5\ kg}$

Lineare Funktion und Regression

1. 
   
   1. 

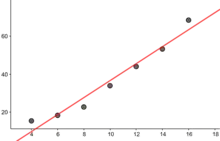      ${\displaystyle G(a)\approx 4{,}47\ a-8{,}1\ }$ (a in Jahre G in Kg)
   2. Gewicht bei Geburt, ${\displaystyle ca.\ -8{,}1,\ }$sinnlos
   3. EXP: ${\displaystyle R^{2}\approx 0{,}99,\ }$linear ${\displaystyle R^{2}\approx 0{,}96\ }$
   4. 

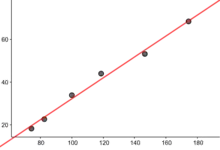      ${\displaystyle G(g)\approx 0{,}49\ g-16{,}9\ }$ (g in cm G in Kg)
   5. Wie viel kg mehr pro cm mehr eine Person wiegt
   6. ${\displaystyle 56{,}7\ -\ 61{,}6}$
   7. ${\displaystyle r\approx 0{,}9956,\ }$fast vollständige Korrelation, die Änderung des Gewichts ist fast ausschließlich durch die Änderung der Größe zu erklären, Kausalität möglich
   8. nein
   9. 2,4 dm, 4 dm, 11,2 dm
   10. 2,4 dm
2. 
   
   1. ${\displaystyle 5\ {\text{W. mit 40 S.}}\qquad \ 8\ {\text{W. mit 65 S.}}\qquad }$
   2. 

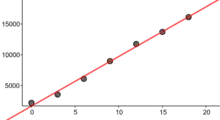      ${\displaystyle Z(t)\approx 805{,}7\ t+1657{,}4\ }$ (t in Jahre seit 2001, Z Anzahl der AbsolventInnen)
   3. Wie viel mehr AbsolventInnen es jedes Jahr gibt
   4. ${\displaystyle r\approx 0{,}9945,\ }$fast vollständige Korrelation, in der Vergangenheit gab es weniger AbsolventInnen und das Wachstum ihre Anzahl hängt extrem mit dem Verlauf der Jahren zusammen, Kausalität ist allerdings nicht vorstellbar
   5. Anzahl der AbsolventInnen im Jahr 2001, ca. 1657, sinnvoll
   6. ca. 2025
   7. nein
   8. ja
   9. 1800, 3000 bzw. 8400 AbsolventInnen
   10. 1800 AbsolventInnen
3. 
   
   1. 

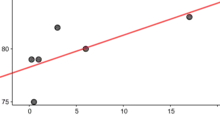      ${\displaystyle T(h)\approx 0{,}302\ h-78{,}27\ }$ (h für Häufigkeit, T in Jahren)
   2. Todesalter bei Zölibat, ${\displaystyle ca.\ 78{,}27,\ }$möglich
   3. EXP: ${\displaystyle R^{2}\approx 0{,}477,\ }$linear ${\displaystyle R^{2}\approx 0{,}480\ }$
   4. 

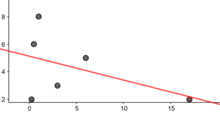      ${\displaystyle B(h)\approx -0{,}17\ g+5{,}13\ }$ (h für Häufigkeit, B Bierflaschen pro Woche)
   5. Wie viel Flaschen weniger getrunken werden, wenn ein mal mehr Sex gemacht wird (pro Woche)
   6. ${\displaystyle 5{,}47\ mal}$
   7. ${\displaystyle r\approx 0{,}9956,\ }$mittlere Korrelation, schwache Zusammenhang, die Kausalität könnte lauten: Je mehr Sex, desto weniger (Lust auf) Bier, sie könnte auch vekehrt sein: je mehr Bier, desto weniger Sex (Alkohol beeinflüsst die Sexualität tatsächlich negativ)
   8. nein
   9. 4,5, 10,5 bzw. 21 Gläser pro Woche
   10. 4,5 Gläser pro Woche
4. 
   
   1. ${\displaystyle 11\ {\text{F. mit 130 P.}}\qquad \ 15\ {\text{F. mit 150 P.}}\qquad }$
   2. 

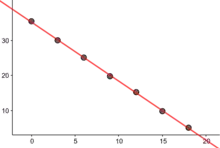      ${\displaystyle Z(t)\approx -1{,}67\ t+35{,}2\ }$ (t in Jahre seit 2001, Z Anzahl der Zigaretten)
   3. Wie viele Zigaretten mehr durchschnittlich täglich geraucht werden, wenn jemand ein Jahr früher stirbt
   4. ${\displaystyle r\approx 0{,}9998,\ }$fast vollständige Korrelation, die Änderung des Todesjahres ist fast ausschließlich durch die Änderung der täglichen Zigarettenanzahl zu erklären, Kausalität möglich
   5. Wann ein nicht Raucher durchschnittlich stirbt, ca. 21, also im Jahr 2022, sinnvoll
   6. ca. 1998
   7. ja
   8. ja
   9. 6%, 14%, 28%
   10. 6%

Darstellungen der linearen Funktion

1. 1. ${\displaystyle 2x-3y-15=0,\quad {\tbinom {x}{y}}={\tbinom {3}{2}}t+{\tbinom {0}{-5}}}$
   2. ${\displaystyle y=-{\tfrac {5}{2}}\ x+{\tfrac {13}{2}},\quad {\tbinom {x}{y}}{}={\tbinom {-2}{5}}t+{\tbinom {0}{6{,}5}}}$
   3. ${\displaystyle y={\tfrac {4}{3}}\ x+3,\quad 4x-3y+9=0}$
   4. ${\displaystyle 58{,}67^{\circ }}$
2. 1. ${\displaystyle 4\ x+7\ y+3=0,\quad {\tbinom {x}{y}}={\tbinom {7}{-4}}t+{\tbinom {0}{-{\tfrac {3}{7}}}}}$
   2. ${\displaystyle y=m\ x+n,\quad {\tbinom {x}{y}}{}={\tbinom {1}{m}}t+{\tbinom {0}{n}}}$
   3. ${\displaystyle y=-{\tfrac {1}{m}}\ x+n,\quad x+m\ y-m\ n=0}$
   4. ${\displaystyle 90^{\circ }}$(senkrecht)
3. 1. ${\displaystyle n\ x-m\ y-m\ c=0,\quad {\tbinom {x}{y}}={\tbinom {m}{n}}t+{\tbinom {0}{c}}}$
   2. ${\displaystyle y=-{\tfrac {5}{c}}\ x-{\tfrac {13}{c}},\quad {\tbinom {x}{y}}{}={\tbinom {c}{5}}t+{\tbinom {0}{13}}}$
   3. ${\displaystyle y={\tfrac {n}{m}}\ x+n,\quad {\tfrac {n}{m}}\ x-y+n=0}$
   4. ${\displaystyle 0^{\circ }}$(parallel)
4. 1. ${\displaystyle b\ x-y-5=0,\quad {\tbinom {x}{y}}={\tbinom {1}{b}}t+{\tbinom {0}{-5}}}$
   2. ${\displaystyle y={\tfrac {2}{q}}\ x-{\tfrac {w}{q}},\quad {\tbinom {x}{y}}={\tbinom {q}{2}}t+{\tbinom {0}{-{\tfrac {w}{q}}}}}$
   3. ${\displaystyle y=-{\tfrac {q\ x}{2}}+{\tfrac {3q}{2}}+4,\quad q\ x+y-3\ q-4=0}$
   4. ${\displaystyle 90^{\circ }}$(normal)
5. 1. ${\displaystyle 0{,}3x-y-5=0,\quad {\tbinom {x}{y}}={\tbinom {1}{0{,}3}}t+{\tbinom {0}{-5}}}$
   2. ${\displaystyle y={\tfrac {5x}{6}}\ +{\tfrac {13}{3}},\quad {\tbinom {x}{y}}={\tbinom {6}{5}}t+{\tbinom {0}{13}}}$
   3. ${\displaystyle y=-2\ x+9,\quad 2x+y-9=0}$
   4. ${\displaystyle 103{,}24^{\circ }}$
6. 1. ${\displaystyle {\sqrt {5}}\ x-y+3=0,\quad {\tbinom {x}{y}}={\tbinom {1}{\sqrt {5}}}t+{\tbinom {0}{3}}}$
   2. ${\displaystyle y=\ x-13,\quad {\tbinom {x}{y}}={\tbinom {1}{1}}t+{\tbinom {0}{-13}}}$
   3. ${\displaystyle y=-{\tfrac {x}{2}}-{\tfrac {7}{2}},\quad x+2y+7=0}$
   4. ${\displaystyle 71{,}57^{\circ }}$

Schnittpunkte von Funktionen in einem Diagramm

1. 1. f:{2}, g:{4,6}, r:{−0,3; 0,4; 5; 6,6; 7,4}, p:{}, h:{}, q{5}.
   2. f:{−2}, g:{2,8}, r:{−2}, p:{3}, q:{−4,4}, h{2,4}.
   3. i) {(3|1)}
      ii) {(−0,4|3,5), (0,7|2,4), (2|2),(4|3), (3,8|2,8)}
      iii) {(0,8|2,4)}${\displaystyle \qquad }$iv){}
      v) {(0|4), (2,7|0,7), (3|1), (4,5|2,5)}
      vi) {(−1,2|3,6), (3|1)}
2. 1. f:{4}, g:{1,5}, r:{−0,45; 0,62; 1,3; 2,9; 3,62}, p:{}, h:{1,3; 2,7}, q{5}.
   2. f:{2}, g:{−2}, r:{5}, p:{5}, q:{?}, h{?}.
   3. i) {(2|1)}
      ii) {(0|5), (1,6|2), (2,7|2,5), (3,8|5)}
      iii) {(3,2|3,4)}${\displaystyle \qquad }$iv){}
      v) {(−0,4|2,2), (0,4|1,8), (1,5|1,3), (2,9|0,6), (3,65|0,2)}
      vi) {(2|1), (1|−1)}
3. 1. f:{0}, g:{10}, r:{−1,5}, p:{}, h:{}, q{3; 7}.
   2. f:{0}, g:{3,3}, r:{5}, p:{5}, q:{?}, h{3,8}.
   3. i) {(4|2)}
      ii) {(0|5), (2|2), (4|5)}
      iii) {(0,7|3,1), (2,7|2,3)}${\displaystyle \qquad }$iv){(4|2), (5,2|2,4)}
      v) {(−0,6|−0,8), (6,8|3,4), (9|4,5)}
      vi) {(1|3), (4|2)}
4. 1. f:{1,6}, h:{6}, g:{−2,6; 2,2; 4,5}, e:{}, c:{1,1; 6}, d{−2,2; 6}.
   2. f:{2,5}, g:{2,5}, h:{−4}, e:{0,6}, c:{2}, d{1,2}.
   3. i) {(3|−2)}
      ii) {(−2,6|−0,5), (1,2|1,6), (4,6|0,8)}
      iii) {(3|−2), (−1|4)}${\displaystyle \qquad }$iv){}
      v) {(0|2,5), (3|−2), (3,6|−3)}
      vi) {(0,3|1,4), (6|0)}

Schnittpunkte von Funktionen in einem Text

1. 1. g:{${\displaystyle \textstyle {\frac {3}{2}}}$}, f:{0}, q{±4}, p:{0; 0,5}, h:{}.
   2. g:{−3}, f:{0}, q:{0,64}, p:{−1}, h{1}.
   3. ja für p, nein für den Rest.
   4. g: s=2 ${\displaystyle \ \ \ }$f: s=${\displaystyle \textstyle -{\frac {7}{3}}}$
   5. i) ${\displaystyle \textstyle \left({\frac {9}{13}}|{\frac {21}{13}}\right)\qquad }$ii) {}${\displaystyle \qquad }$iii) {}
2. 1. g:{5}, f:{−10}, q{}, p:{}, h:{2±2${\displaystyle {\sqrt {2}}}$}.
   2. g:{2}, f:{${\displaystyle 0{,}{\dot {6}}}$}, q:{0,49}, p:{2}, h{−1}.
   3. nein
   4. g: s=−0,4 ${\displaystyle \ \ \ }$f: s=${\displaystyle \textstyle 0{,}0{\dot {6}}}$
   5. i) ${\displaystyle \textstyle \left({\frac {20}{7}}|{\frac {6}{7}}\right)\qquad }$ii) {}${\displaystyle \qquad }$
      iii) {${\displaystyle \textstyle \left({\frac {10+{\sqrt {1531}}}{27}}{\big |}{\frac {280+{\sqrt {1531}}}{405}}\right)}$,${\displaystyle \textstyle \ \left({\frac {10-{\sqrt {1531}}}{27}}{\big |}{\frac {280-{\sqrt {1531}}}{405}}\right)}$}
3. 1. g:{${\displaystyle \textstyle -{\frac {2}{43}}}$}, f:{2,5}, q{0; 1,6}, p:{±0,75}, h:{}.
   2. g:{${\displaystyle -{\frac {1}{21}}}$}, f:{0,5}, q:{0}, p:{−2,25}, h{2}.
   3. ja für g und p, nein für den Rest.
   4. g: s=${\displaystyle \textstyle -{\frac {43}{42}}}$ ${\displaystyle \ \ \ }$f: s=−0,2
   5. i) {${\displaystyle \textstyle \left(-{\frac {115}{173}}|{\frac {219}{346}}\right)}$}${\displaystyle \qquad }$iii) { ${\displaystyle \textstyle \left(-{\frac {37}{42}}|{\frac {1507}{1764}}\right)}$,${\displaystyle \quad \textstyle \left({\frac {5}{8}}|-{\frac {11}{16}}\right)}$}
      ii) {${\displaystyle \textstyle \left({\frac {-5+5{\sqrt {190}}}{84}}{\big |}{\frac {403-25{\sqrt {190}}}{882}}\right)}$,${\displaystyle \textstyle \ \left({\frac {-5-5{\sqrt {190}}}{84}}{\big |}{\frac {403+25{\sqrt {190}}}{882}}\right)}$}${\displaystyle \qquad }$
4. 1. g:{${\displaystyle \textstyle {\frac {108}{3}}}$}, f:{${\displaystyle {\tfrac {\sqrt {5}}{\pi }}}$}, q{0; 1,6}, p:{±0,75}, h:{}.
   2. g:{2}, f:{${\displaystyle {\sqrt {5}}}$}, q:{1}, p:{0}, h{−2}.
   3. ja nur für f
   4. g: s=${\displaystyle \textstyle -{\frac {3}{7}}}$ ${\displaystyle \ \ \ }$f: s=${\displaystyle -\pi }$
   5. i) {${\displaystyle \textstyle \left({\frac {7({\sqrt {5}}-2)}{7\pi -3}}|{\frac {14\pi -3{\sqrt {5}}}{7\pi -3}}\right)}$}${\displaystyle \qquad }$ii) { }
      iii) {${\displaystyle \textstyle \left({\frac {{\sqrt {8681}}+29}{140}}{\big |}{\frac {1873-3{\sqrt {8681}}}{980}}\right)}$,${\displaystyle \textstyle \ \left({\frac {-{\sqrt {8681}}+29}{140}}{\big |}{\frac {1873+3{\sqrt {8681}}}{980}}\right)}$}${\displaystyle \qquad }$

Die quadratische Gleichung

1. 1. ${\displaystyle w_{1}=1\ \ }$und ${\displaystyle \ w_{2}=0{,}{\dot {3}}}$
   2. ${\displaystyle \mathbb {L} =\emptyset }$
   3. ${\displaystyle m_{1,\ 2}=-1{,}5}$
2. 1. ${\displaystyle w_{1}=1\ \ }$und ${\displaystyle \ w_{2}=3}$
   2. ${\displaystyle \textstyle c_{1,\ 2}=\pm {\frac {\sqrt {7}}{2}}}$
   3. ${\displaystyle \textstyle m=-{\frac {7}{4}}}$
3. 1. ${\displaystyle \textstyle w_{1}=1\ \ }$und ${\displaystyle \ w_{2}={\frac {1}{5}}}$
   2. ${\displaystyle \textstyle c={\frac {8}{5}}}$
   3. ${\displaystyle m_{1,\ 2}=\pm 5}$
4. 1. ${\displaystyle y={\tfrac {1}{2}}}$
   2. ${\displaystyle k_{1}={\tfrac {3}{5}}\quad k_{2}=-2}$
   3. ${\displaystyle \mathbb {L} =\emptyset }$

Quadratische Gleichung Textaufgaben

1. 1. ${\displaystyle v_{1}\approx 41{,}9\ {\text{oder }}173{,}1\ km/h}$
   2. ${\displaystyle t_{1}\approx 3{,}46\ {\text{oder }}0{,}84\ h}$
2. 1. ${\displaystyle v_{1}\approx 1{,}16\ m^{3}/min}$
   2. ${\displaystyle t_{1}\approx 25{,}96\ min}$
3. 1. ${\displaystyle v\approx 772{,}7\ km/h}$
   2. ${\displaystyle t\approx 21{,}8}$
4. 1. ${\displaystyle v_{1}\approx 32{,}5\ {\text{oder }}125{,}8}$
   2. ${\displaystyle t_{1}\approx 7{,}23\ {\text{oder }}1{,}87\ h}$
5. 1. ${\displaystyle v_{1}\approx 0{,}64\ }$oder${\displaystyle \ 2{,}32\ m^{3}/min}$
   2. ${\displaystyle t_{1}\approx 78{,}2\ }$oder${\displaystyle \ 21{,}6\ min}$
6. 1. ${\displaystyle v_{1}\approx 936{,}0\ km/h}$
   2. ${\displaystyle t\approx 26{,}4\ s}$

Quadratische Funktion Vertiefung

1. ${\displaystyle S:\left(-{\tfrac {7}{8}}|-5{\tfrac {1}{16}}\right);\quad c(k)=(k+2)(k-{\tfrac {1}{4}})}$
2. ${\displaystyle S:\left(-{\tfrac {1}{2}}|-6{\tfrac {1}{4}}\right);\quad b(z)=(z-2)(z+3)}$
3. ${\displaystyle S:\left({\tfrac {1}{2}}|-6{\tfrac {1}{4}}\right);\quad z(x)=(x+2)(x-3)}$
4. ${\displaystyle S:\left(-{\tfrac {1}{2}}|-16\right);\quad c(y)=(y+2{,}5)(y-1{,}5)}$
5. ${\displaystyle S:\left({\tfrac {1}{2}}|-{\tfrac {9}{4}}\right);\quad k(c)=(c+1)(c-2)}$
6. ${\displaystyle S:\left({\tfrac {1}{2}}|-16\right);\quad c(v)=(v-2{,}5)(v+1{,}5)}$

Funktionserkennung in Diagramm

1 → G, 2 → E, 3→ D, 4 → B H
5 → F,6 → B H, 7 → K M N, 8 → A
9 → C, 10 → B H, 11 → L, 12 → A
13 → M, 14 → K, 15 → C D N

Funktionsdiagramme Eigenschaften erkennen

1. Hier klicken!
2. Hier klicken!

Funktionserkennung in Text

1. Hier klicken!