Beweisarchiv: Geometrie: Trigonometrie: Additionstheoreme: Sinus

Kreis: Mittelpunktswinkel-Umfangswinkel · Satz des Ptolemäus · Sehnensatz · Sehnentangentenwinkel · Sehnenviereck · Sekantensatz · Japanischer Satz für konzyklische Vierecke · Satz des Thales

Rechtwinkliges Dreieck: Satz des Pythagoras

Ellipse: Satz vom Flüstergewölbe · Konjugierte Durchmesser

Regelmäßige Vielecke: Dreieck · Viereck · Fünfeck · Sechseck ·

Dreieck: Satz des Heron · Berechnung des Flächeninhalts des Diagonalendreiecks im Quader · Elementarer Satz zur Charakterisierung des Schwerpunkts im Dreieck via Flächeninhalte

Inzidenzgeometrie ·

affine Geometrie: einfache Hilfssätze · Homothetien und Translationen · Desarguesche affine Ebenen sind Vektorräume

Trigonometrie

Additionstheoreme: Sinus · Kosinus · Tangens · Kotangens

Trigonometriesätze: Sinussatz · Kosinussatz · Neue Folgerungen aus dem Projektionssatz der Dreiecksgeometrie

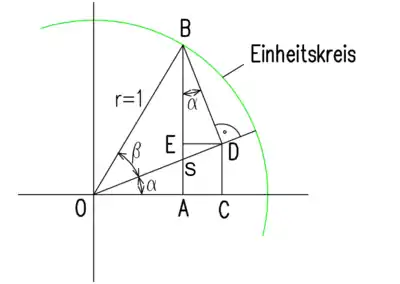
Additionstheoreme (Sinus)

Beweis für:

$\sin(\alpha \pm \beta )=\sin \alpha \cdot \cos \beta \pm \sin \beta \cdot \cos \alpha$

Im rechtwinkligen Dreieck $\triangle {AOB}$ ist

(1) $\sin(\alpha +\beta )={\frac {\overline {AB}}{1}}={\overline {AB}}$

Im rechtwinkligen Dreieck $\triangle {BOD}$ ist

(2) $\sin \beta ={\frac {\overline {BD}}{1}}={\overline {BD}}$

und

(3) $\cos \beta ={\frac {\overline {OD}}{1}}={\overline {OD}}$

Im rechtwinkligen Dreieck $\triangle {OCD}$ ist

(4.1) $\sin \alpha ={\frac {\overline {CD}}{\overline {OD}}}$

(3) eingesetzt

(4.2) $\sin \alpha ={\frac {\overline {CD}}{\cos \beta }}$

(4.3) $\sin \alpha \cdot \cos \beta ={\overline {CD}}$

Dreiecke $\triangle {BSD}$ und $\triangle {OSA}$ sind beide rechtwinkelig
und $\angle {BSD}=\angle {OSA},$ daher:

(5.0) $\angle {SOA}=\angle {SBD}=\alpha$

Im rechtwinkligen Dreieck $\triangle {EDB}$ gilt:

(5.1) $\cos \alpha ={\frac {\overline {BE}}{\overline {BD}}}$

(2) eingesetzt

(5.2) $\cos \alpha ={\frac {\overline {BE}}{\sin \beta }}$

(5.3) $\sin \beta \cdot \cos \alpha ={\overline {BE}}$

(6.1) ${\overline {AB}}={\overline {CD}}+{\overline {BE}}$

(4.3) und (5.3) eingesetzt

(6.2) ${\overline {AB}}=\sin \alpha \cdot \cos \beta +\sin \beta \cdot \cos \alpha$

in (1) eingesetzt

(7) $\sin(\alpha +\beta )=\sin \alpha \cdot \cos \beta +\sin \beta \cdot \cos \alpha$

Wenn Winkel $\beta$ negativ:

(8) $\sin(\alpha -\beta )=\sin \alpha \cdot \cos(-\beta )+\sin(-\beta )\cdot \cos \alpha$

(9a) $\cos(-\beta )=+\cos \beta \,$

und

(9b) $\sin(-\beta )=-\sin \beta \,$

eingesetzt in (8)

(10) $\sin(\alpha -\beta )=\sin \alpha \cdot \cos \beta -\sin \beta \cdot \cos \alpha$

(7) und (10) zusammengefasst

(11) $\sin(\alpha \pm \beta )=\sin \alpha \cdot \cos \beta \pm \sin \beta \cdot \cos \alpha$

Additionstheoreme (Sinus)

Beweis für

$\sin \left(\alpha \pm \beta \right)=\sin \left(\alpha \right)\cdot \cos \left(\beta \right)\pm \sin \left(\beta \right)\cdot \cos \left(\alpha \right)$

Für den Beweis werden die Beziehungen
${\begin{aligned}\sin \left(\alpha \right)&={\frac {1}{2\cdot {\mathsf {i}}}}\cdot \left({\mathsf {e}}^{{\mathsf {i}}\cdot \alpha }-{\mathsf {e}}^{-{\mathsf {i}}\cdot \alpha }\right)\\\cos \left(\alpha \right)&={\frac {1}{2}}\cdot \left({\mathsf {e}}^{{\mathsf {i}}\cdot \alpha }+{\mathsf {e}}^{-{\mathsf {i}}\cdot \alpha }\right)\end{aligned}}$
verwendet.

Es gilt:
${\begin{aligned}\sin \left(\alpha \pm \beta \right)&=\sin \left(\alpha \right)\cdot \cos \left(\beta \right)\pm \sin \left(\beta \right)\cdot \cos \left(\alpha \right)\\&={\frac {1}{2\cdot {\mathsf {i}}}}\cdot \left({\mathsf {e}}^{{\mathsf {i}}\cdot \alpha }-{\mathsf {e}}^{-{\mathsf {i}}\cdot \alpha }\right)\cdot {\frac {1}{2}}\cdot \left({\mathsf {e}}^{{\mathsf {i}}\cdot \beta }+{\mathsf {e}}^{-{\mathsf {i}}\cdot \beta }\right)\pm {\frac {1}{2\cdot {\mathsf {i}}}}\cdot \left({\mathsf {e}}^{{\mathsf {i}}\cdot \beta }-{\mathsf {e}}^{-{\mathsf {i}}\cdot \beta }\right)\cdot {\frac {1}{2}}\cdot \left({\mathsf {e}}^{{\mathsf {i}}\cdot \alpha }+{\mathsf {e}}^{-{\mathsf {i}}\cdot \alpha }\right)\\&={\frac {1}{4\cdot {\mathsf {i}}}}\cdot \left(\left({\mathsf {e}}^{{\mathsf {i}}\cdot \alpha }-{\mathsf {e}}^{-{\mathsf {i}}\cdot \alpha }\right)\cdot \left({\mathsf {e}}^{{\mathsf {i}}\cdot \beta }+{\mathsf {e}}^{-{\mathsf {i}}\cdot \beta }\right)\pm \left({\mathsf {e}}^{{\mathsf {i}}\cdot \beta }-{\mathsf {e}}^{-{\mathsf {i}}\cdot \beta }\right)\cdot \left({\mathsf {e}}^{{\mathsf {i}}\cdot \alpha }+{\mathsf {e}}^{-{\mathsf {i}}\cdot \alpha }\right)\right)\\&={\frac {1}{4\cdot {\mathsf {i}}}}\cdot \left({\mathsf {e}}^{{\mathsf {i}}\cdot \left(\alpha +\beta \right)}+{\mathsf {e}}^{{\mathsf {i}}\cdot \left(\alpha -\beta \right)}-{\mathsf {e}}^{-{\mathsf {i}}\cdot \left(\alpha -\beta \right)}-{\mathsf {e}}^{-{\mathsf {i}}\cdot \left(\alpha +\beta \right)}\pm {\mathsf {e}}^{{\mathsf {i}}\cdot \left(\alpha +\beta \right)}\pm {\mathsf {e}}^{-{\mathsf {i}}\cdot \left(\alpha -\beta \right)}\mp {\mathsf {e}}^{{\mathsf {i}}\cdot \left(\alpha -\beta \right)}\mp {\mathsf {e}}^{-{\mathsf {i}}\cdot \left(\alpha +\beta \right)}\right)\\&={\frac {1}{4\cdot {\mathsf {i}}}}\cdot \left(\left(1\pm 1\right)\cdot {\mathsf {e}}^{{\mathsf {i}}\cdot \left(\alpha +\beta \right)}+\left(1\mp 1\right)\cdot {\mathsf {e}}^{{\mathsf {i}}\cdot \left(\alpha -\beta \right)}-\left(1\mp 1\right)\cdot {\mathsf {e}}^{-{\mathsf {i}}\cdot \left(\alpha -\beta \right)}-\left(1\pm 1\right)\cdot {\mathsf {e}}^{-{\mathsf {i}}\cdot \left(\alpha +\beta \right)}\right)\\&={\frac {1}{2\cdot {\mathsf {i}}}}\cdot \left({\mathsf {e}}^{{\mathsf {i}}\cdot \left(\alpha \pm \beta \right)}-{\mathsf {e}}^{-{\mathsf {i}}\cdot \left(\alpha \pm \beta \right)}\right)\end{aligned}}$
Die Umformung zum vorletzten Schritt ist zulässig, da entweder $\left(1\pm 1\right)\cdot {\mathsf {e}}^{\pm {\mathsf {i}}\cdot \left(\alpha +\beta \right)}$ oder $\left(1\mp 1\right)\cdot {\mathsf {e}}^{\pm {\mathsf {i}}\cdot \left(\alpha -\beta \right)}$ auftritt.

Beweisarchiv: Geometrie

Schwerpunktsätze von Leibniz

Planimetrie