Beweisarchiv: Geometrie

Schwerpunktsätze von Leibniz

Planimetrie

Kreis: Mittelpunktswinkel-Umfangswinkel · Satz des Ptolemäus · Sehnensatz · Sehnentangentenwinkel · Sehnenviereck · Sekantensatz · Japanischer Satz für konzyklische Vierecke · Satz des Thales

Rechtwinkliges Dreieck: Satz des Pythagoras

Ellipse: Satz vom Flüstergewölbe · Konjugierte Durchmesser

Regelmäßige Vielecke: Dreieck · Viereck · Fünfeck · Sechseck ·

Dreieck: Satz des Heron · Berechnung des Flächeninhalts des Diagonalendreiecks im Quader · Elementarer Satz zur Charakterisierung des Schwerpunkts im Dreieck via Flächeninhalte

Inzidenzgeometrie ·

affine Geometrie: einfache Hilfssätze · Homothetien und Translationen · Desarguesche affine Ebenen sind Vektorräume

Trigonometrie

Additionstheoreme: Sinus · Kosinus · Tangens · Kotangens

Trigonometriesätze: Sinussatz · Kosinussatz · Neue Folgerungen aus dem Projektionssatz der Dreiecksgeometrie

Sehnentangentenwinkelsatz

Der Sehnentangentenwinkel eines Kreisbogens ist so groß wie der zugehörigen Umfangswinkel (Peripheriewinkel) und halb so groß wie der zugehörige Mittelpunktswinkel (Zentriwinkel).

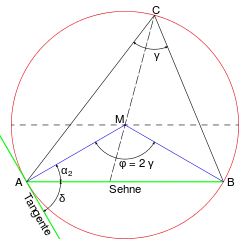
Sehnentangentenwinkel

Nachweis, dass der Sehnentangentenwinkel gleich dem Umfangswinkel ist:

(Siehe Skizze)

Der Mittelpunktswinkel ist doppelt so groß wie der Umfangswinkel (siehe weiter oben):

${\displaystyle \varphi =2\gamma }$

Winkelsumme im gleichschenkligen ${\displaystyle \bigtriangleup {AMB}}$:

${\displaystyle 2\alpha _{2}+2\gamma =180^{\circ }\,}$

${\displaystyle \alpha _{2}={\frac {180^{\circ }-2\gamma }{2}}=90^{\circ }-\gamma }$

Sehnentangentenwinkel:

${\displaystyle \delta =90^{\circ }-\alpha _{2}=90^{\circ }-(90^{\circ }-\gamma )}$

${\displaystyle \delta =\gamma \,}$