| ||||||||||||||||
Theorie in Kürze (mit Geogebra)
- Integral Fläche
- Geogebra: Integral(Funktion ohne f(x) schreiben, )
- Bei entsprechenden Aufgaben entsprechende Fläche schraffieren.
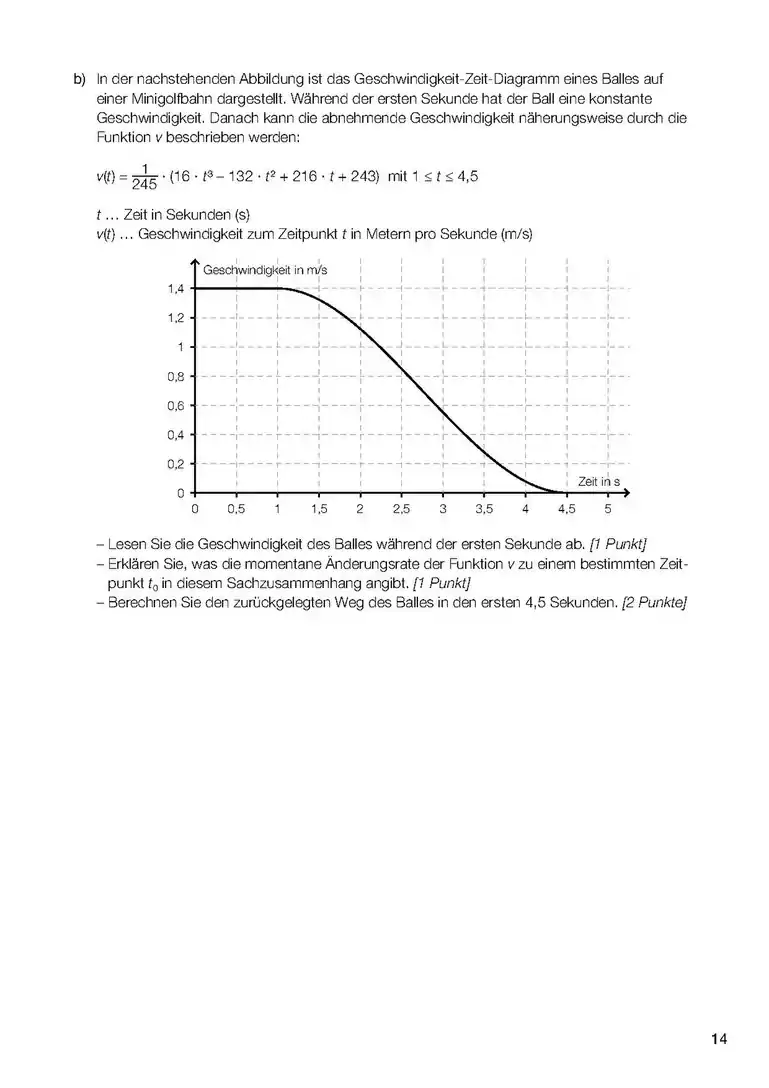
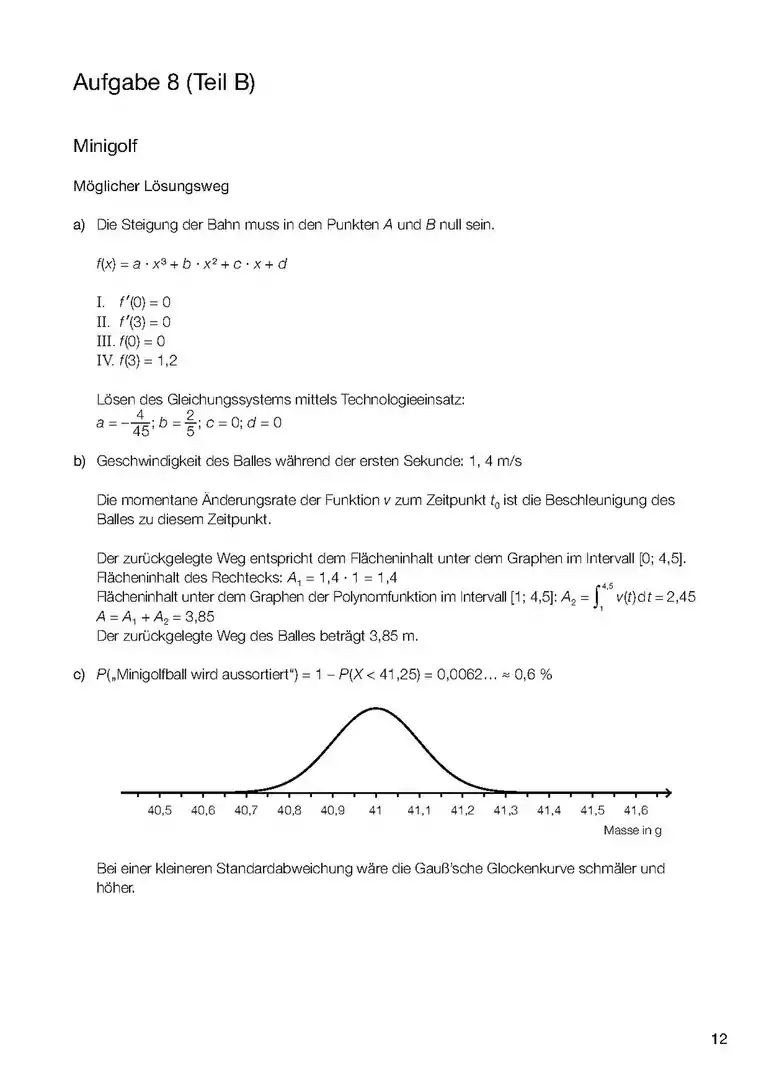
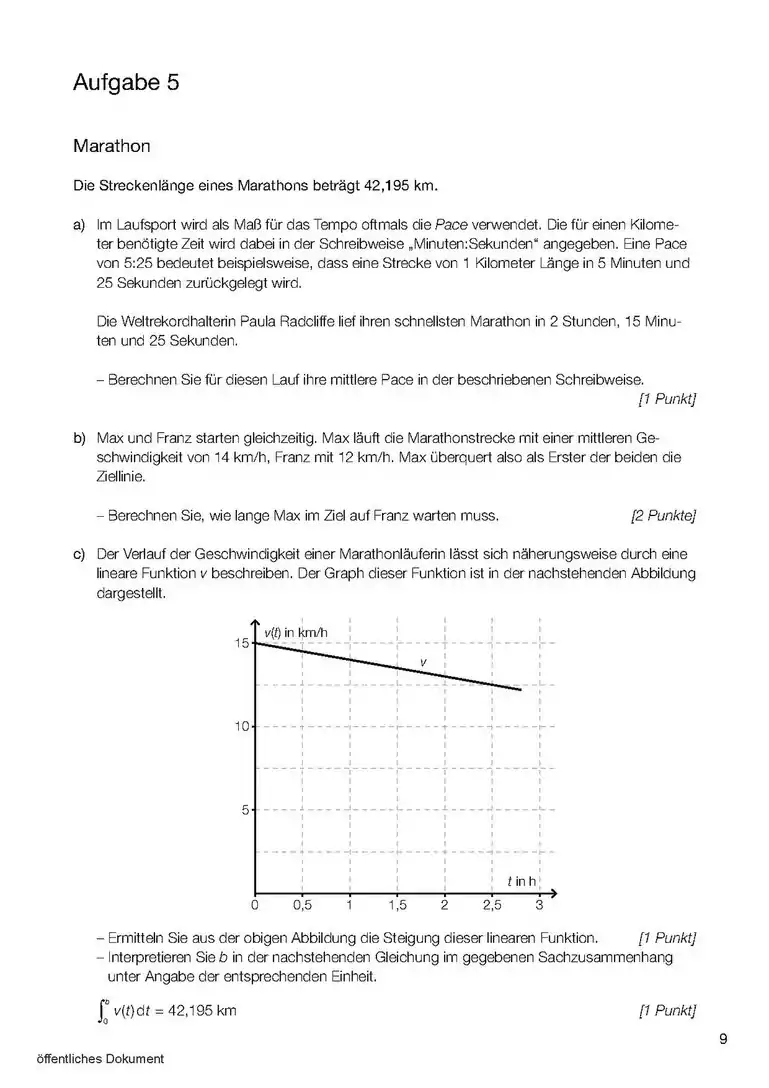
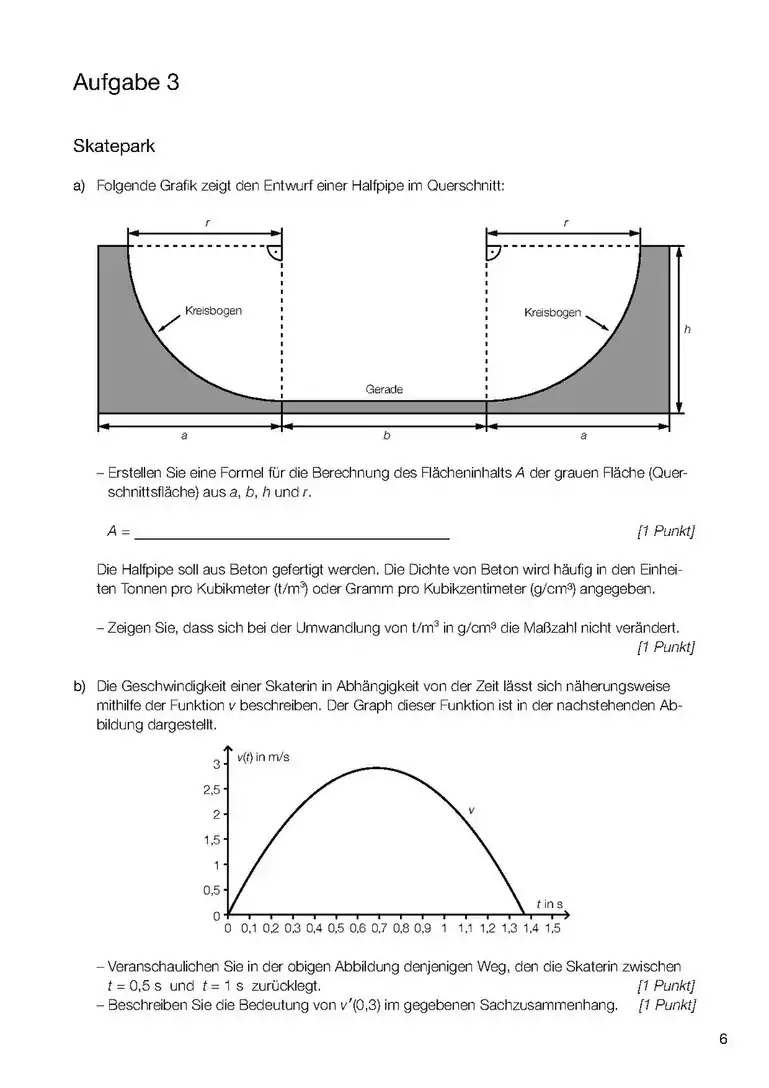
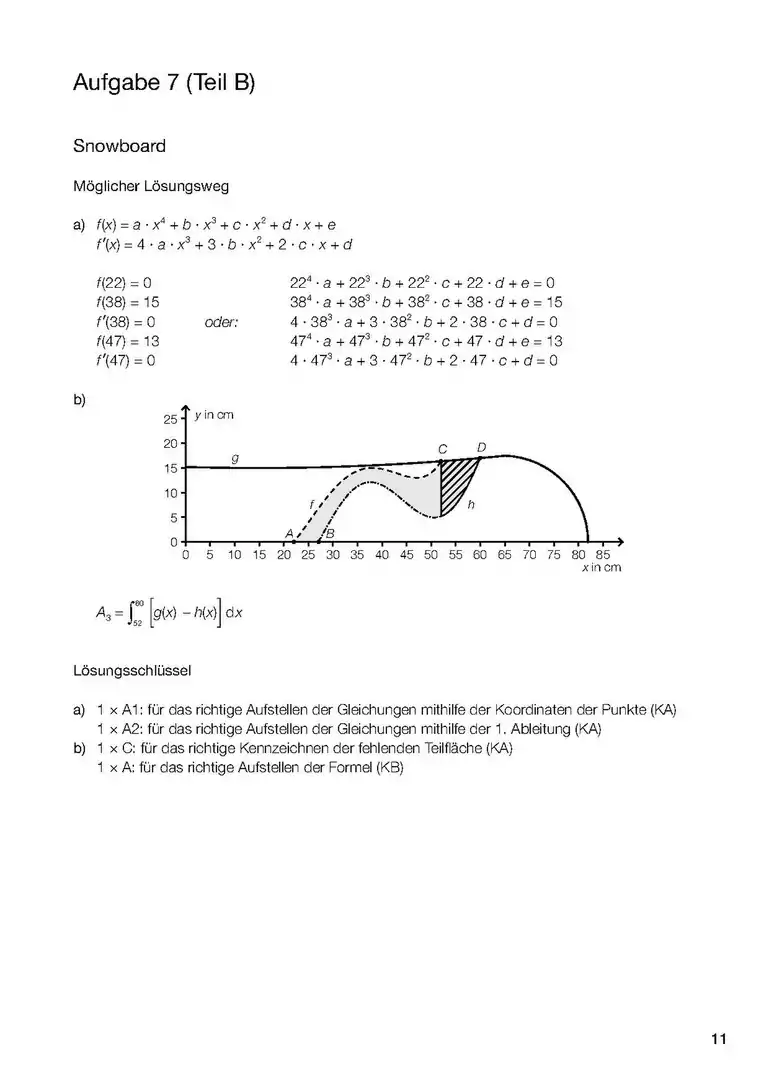
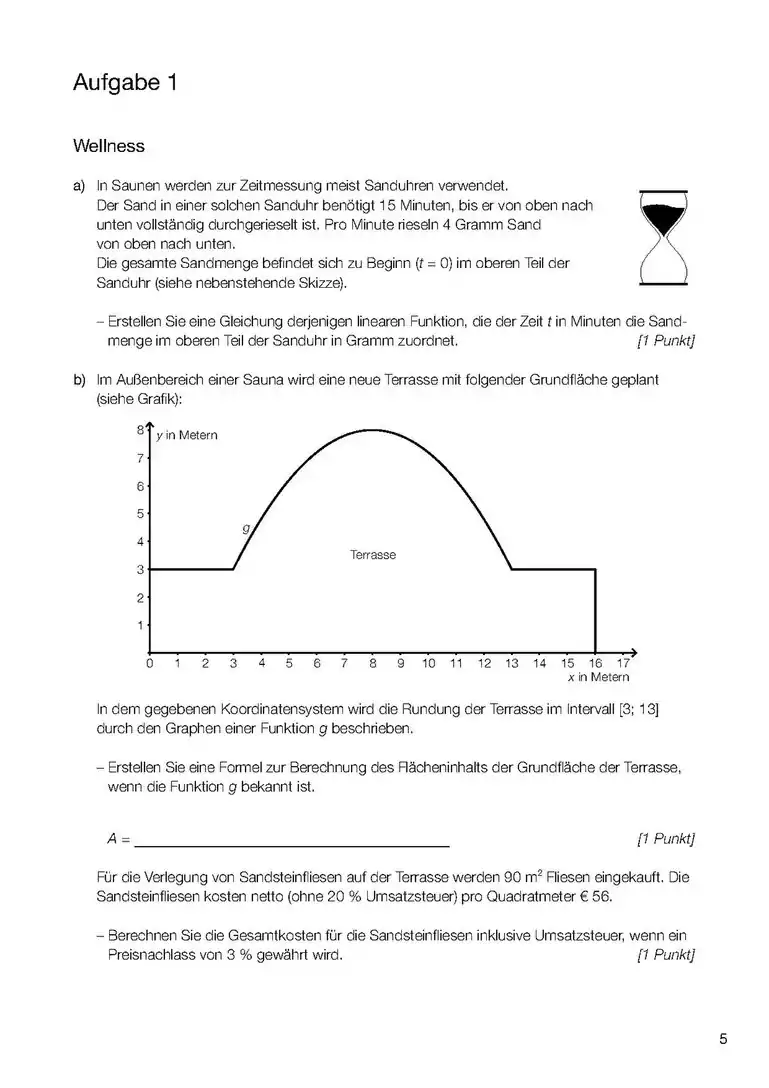
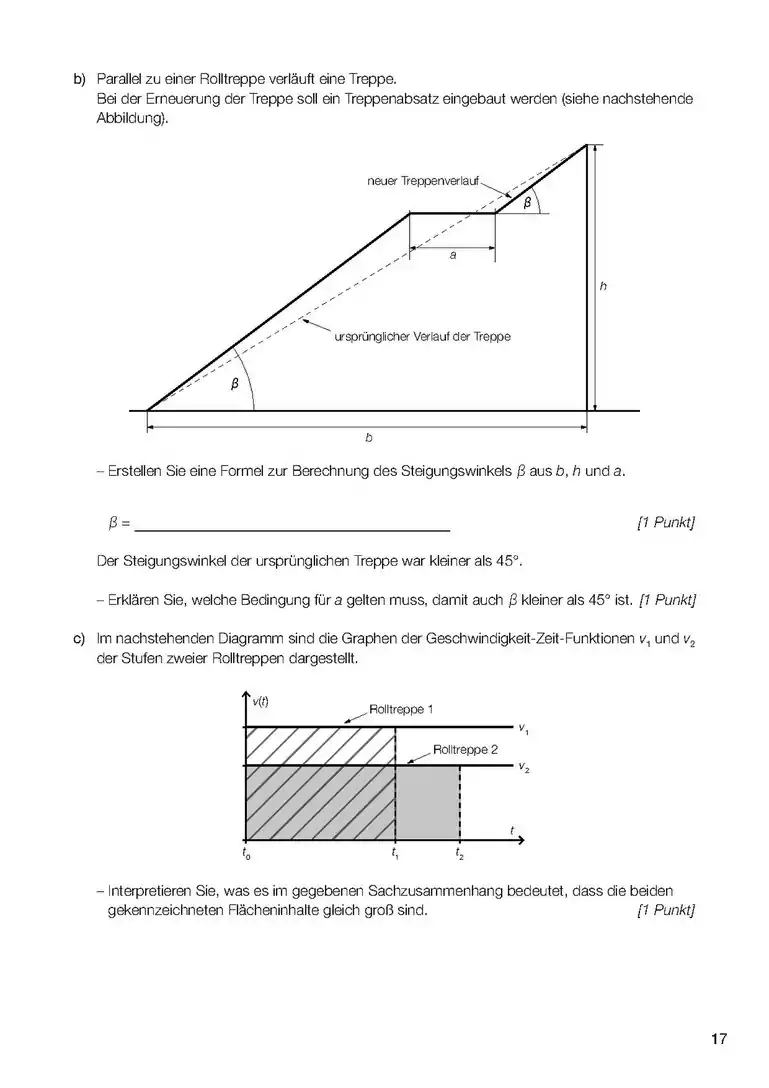
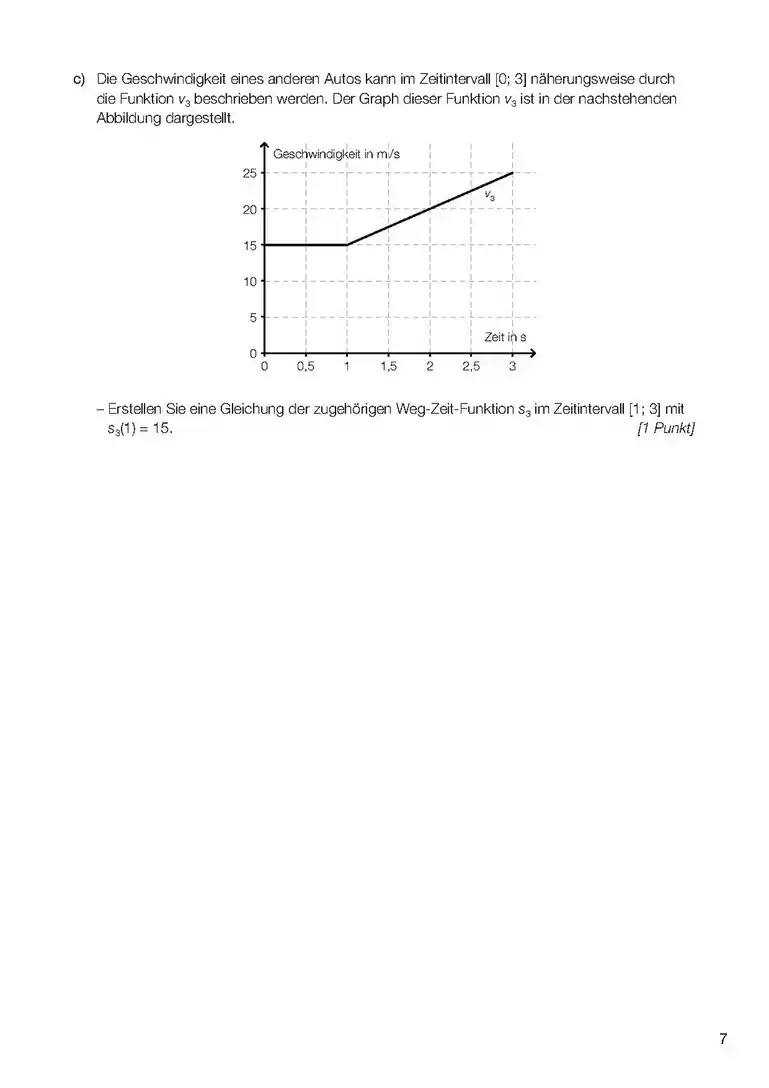
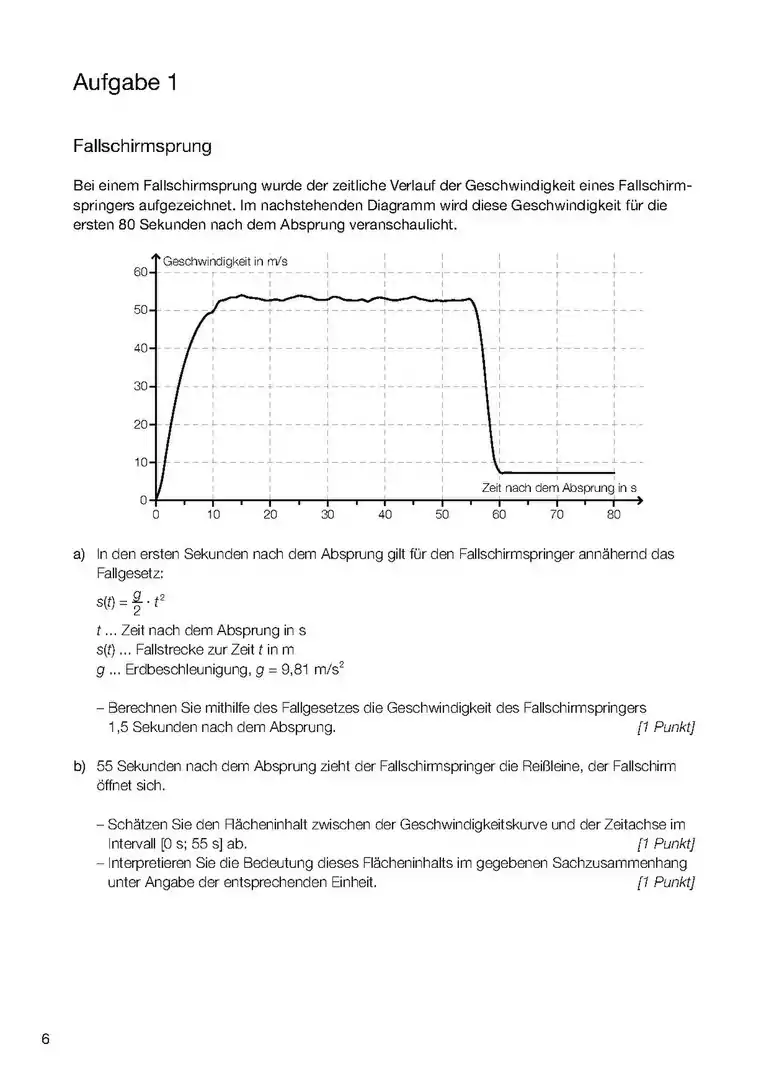
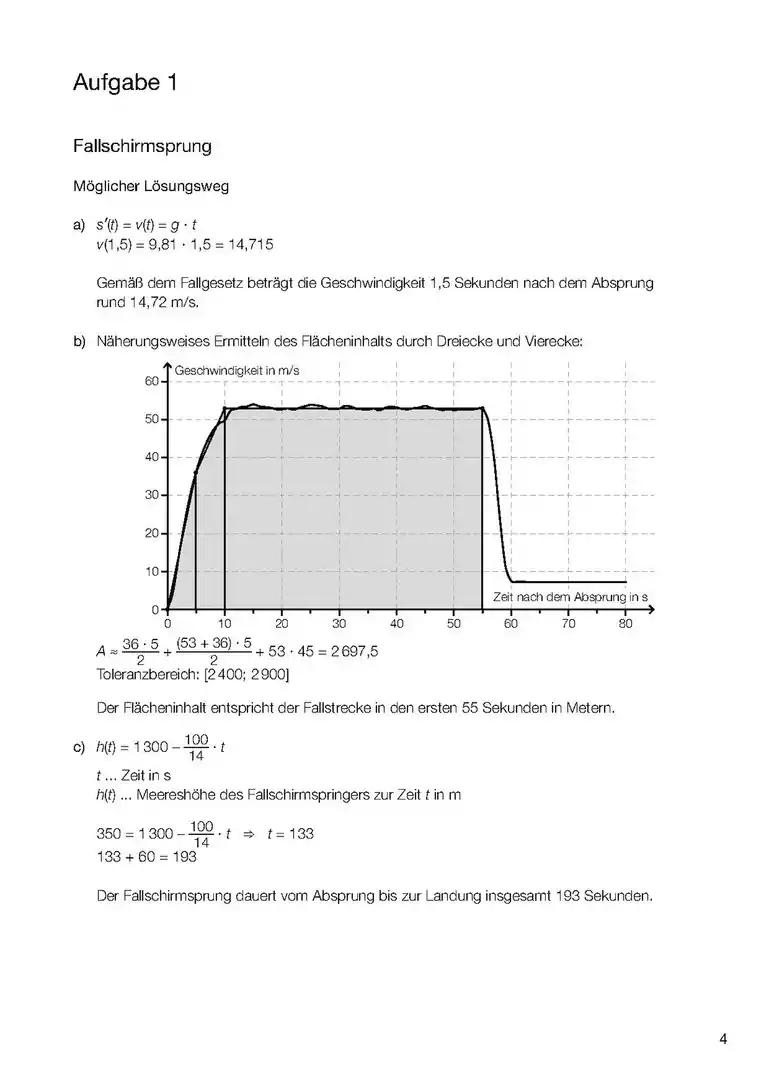
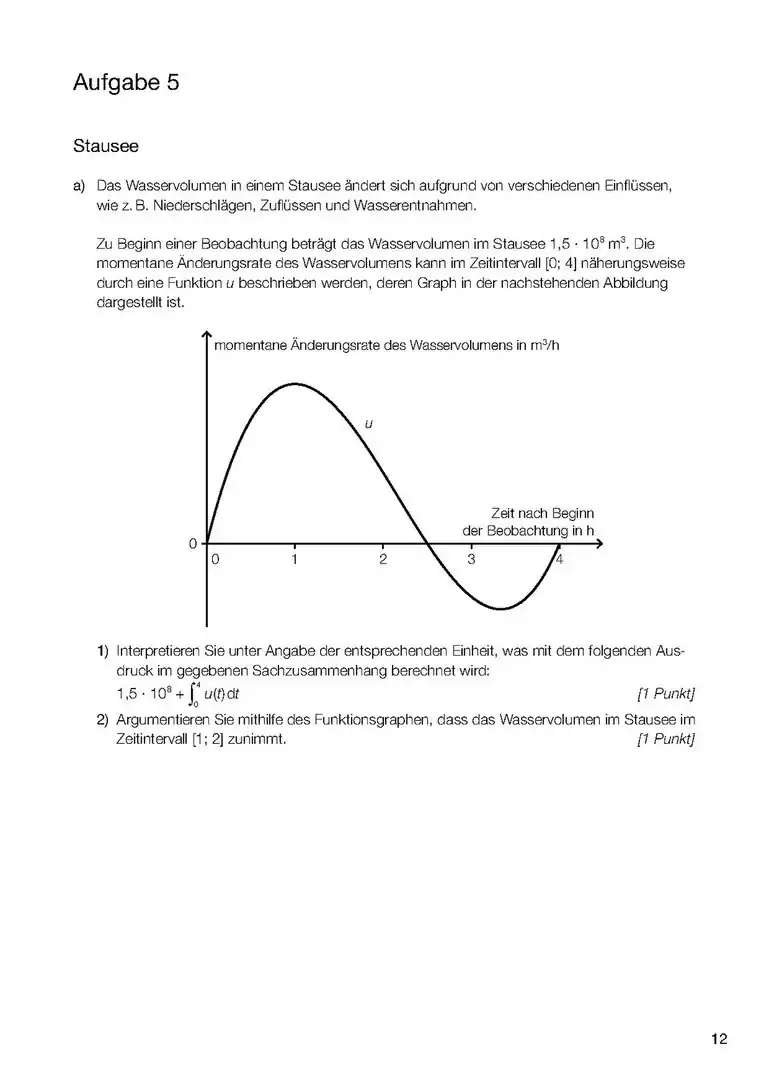
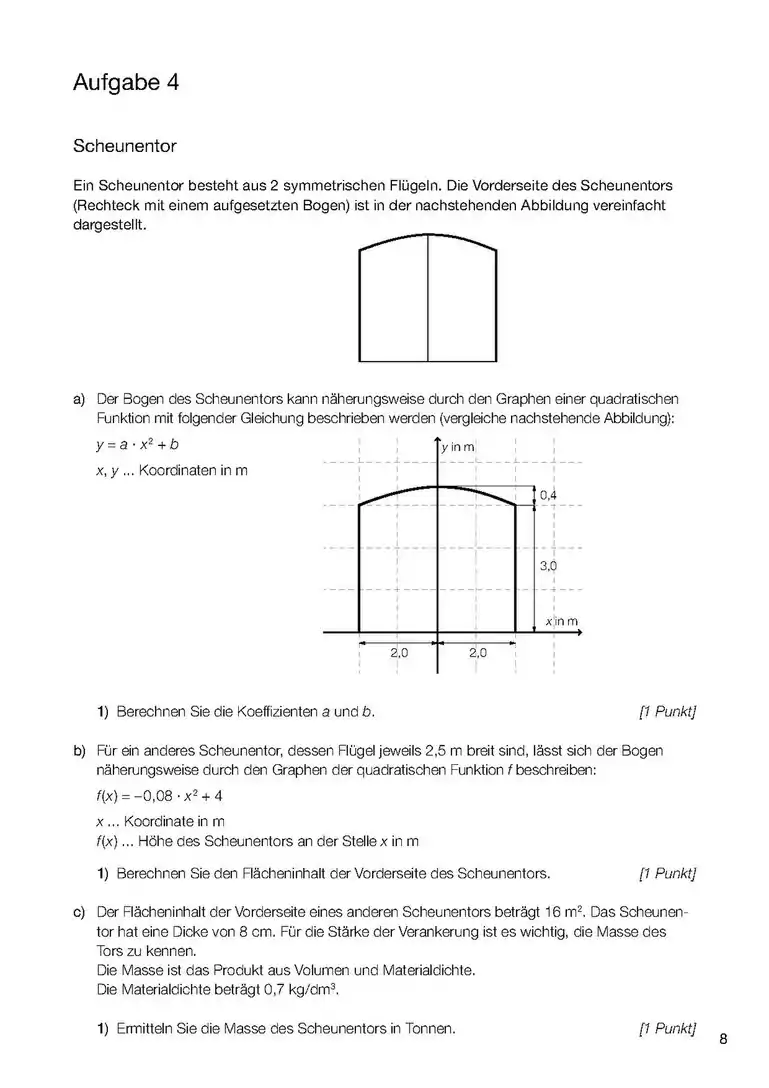
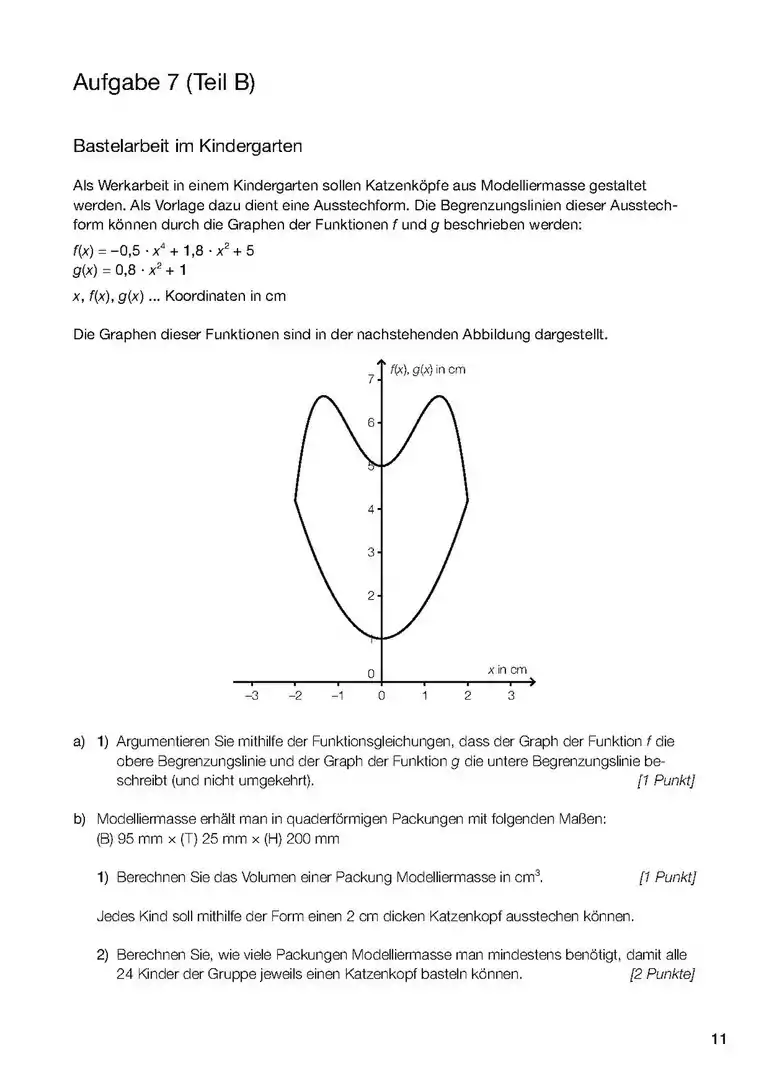
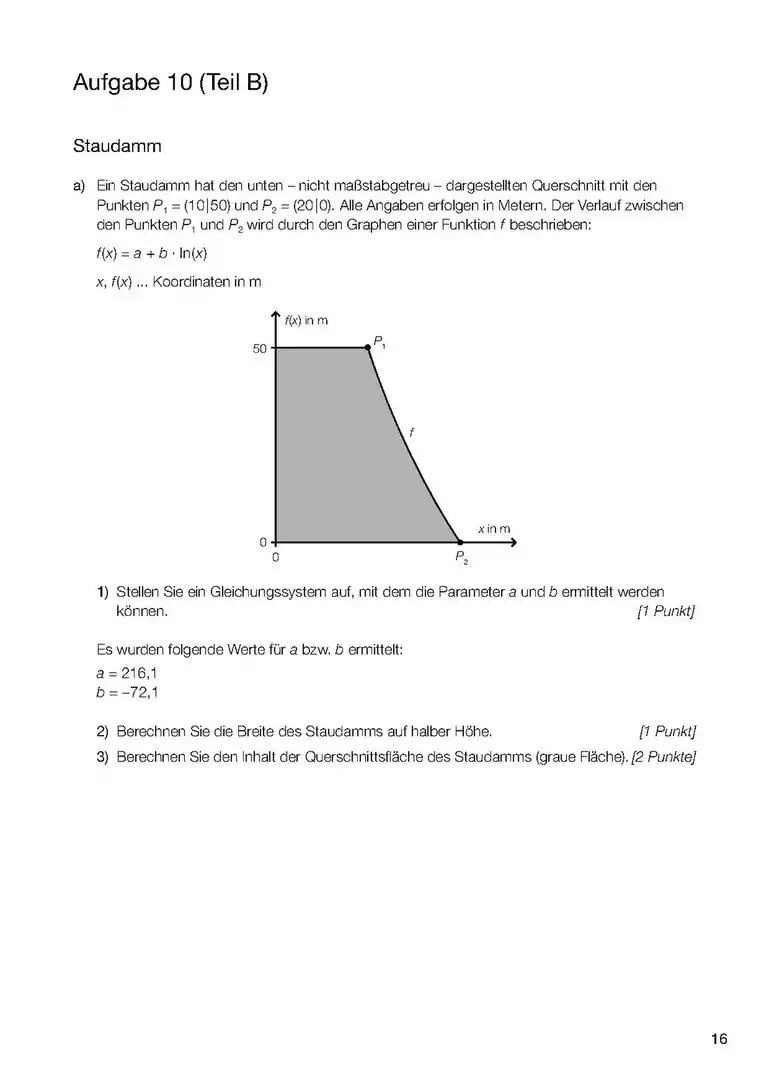
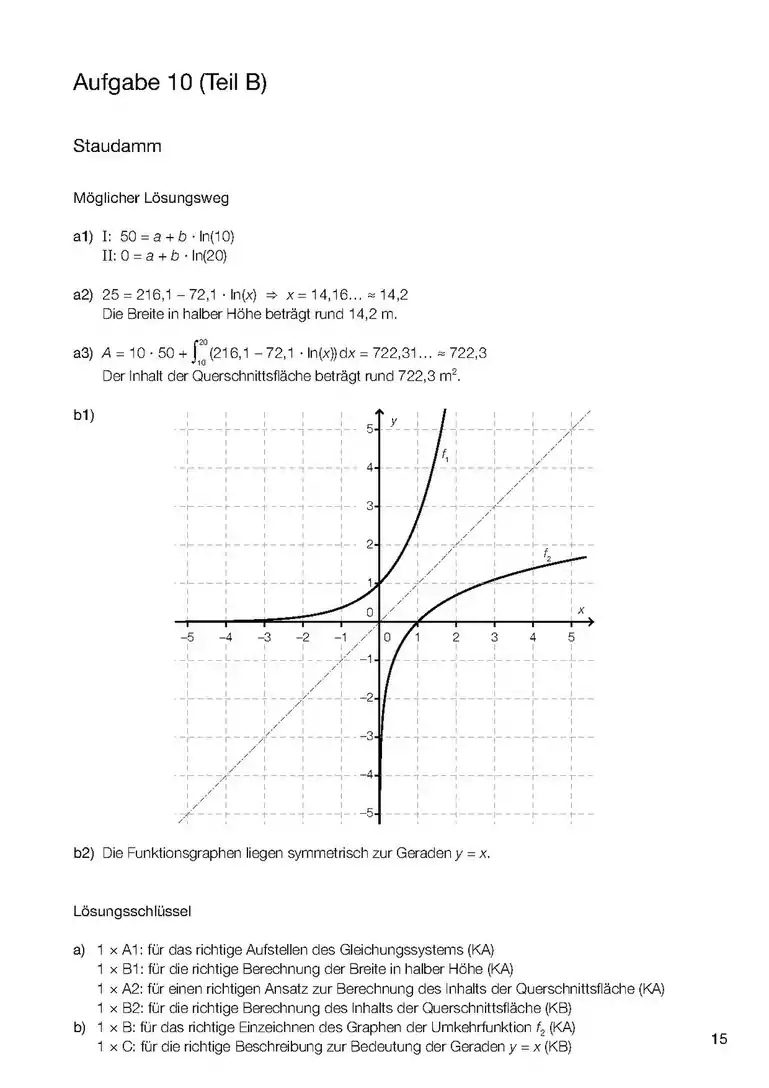
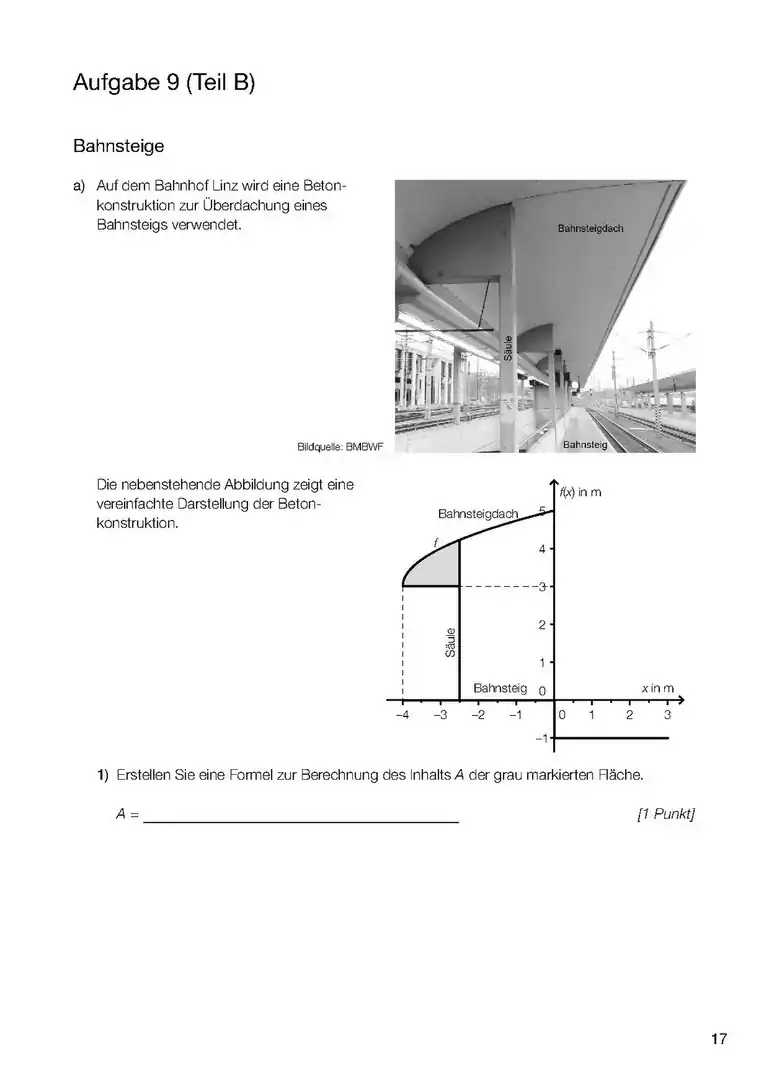
- Wenn es um das Integral einer Funktion (und nicht einer Differen)z geht, dann ist das Integral dieser Funktion die Fläche zwischen Kurve und x-Achse und zwischen den Grenzen (Stellen, x-Werte), die im Integral angegeben werden. (1. Bild). sind daher hier Werte von x (Stellen) also ein Intervall [a;b] zwischen a und b auf der x-Achse, das die seitlichen (links und rechts) Grenzen des Integrals angibt. Die Funktion f(x) kann auch eine Zahl sein (!), z.B ist die Fläche zwischen der Gerade y=3 (parallel zur x-Achse) und zwischen x=a und x=b, also die Fläche eines Rechtecks im Diagramm (ähnlich wie im 2. Bild).
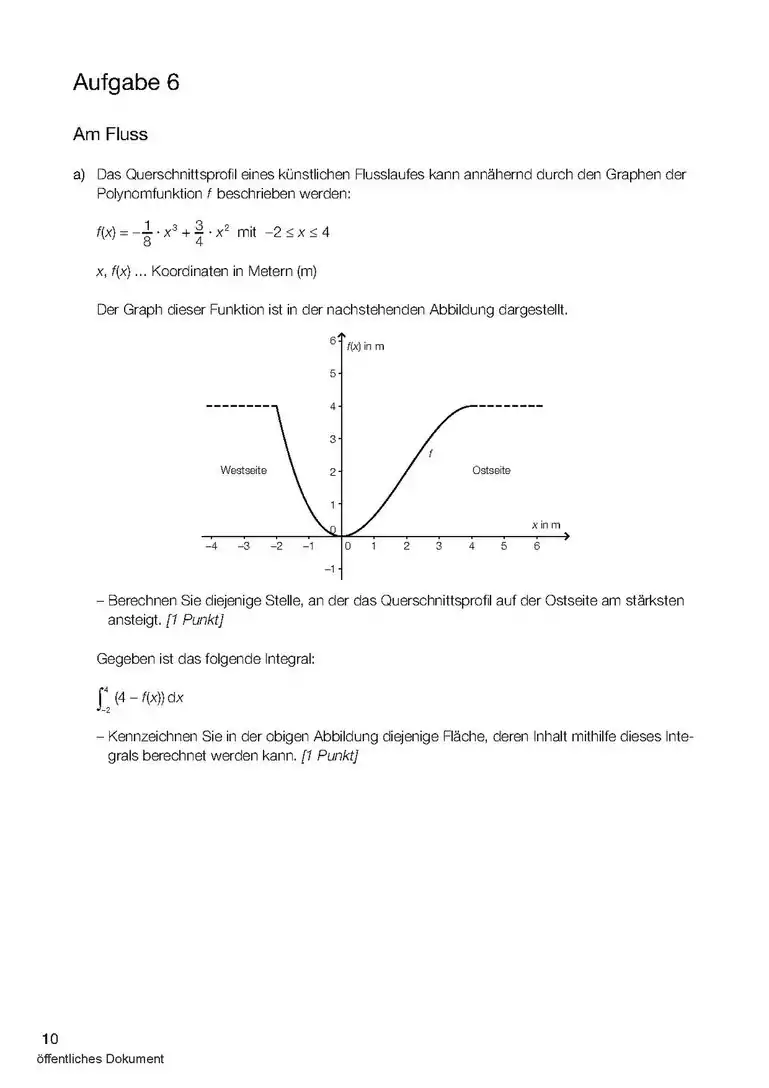
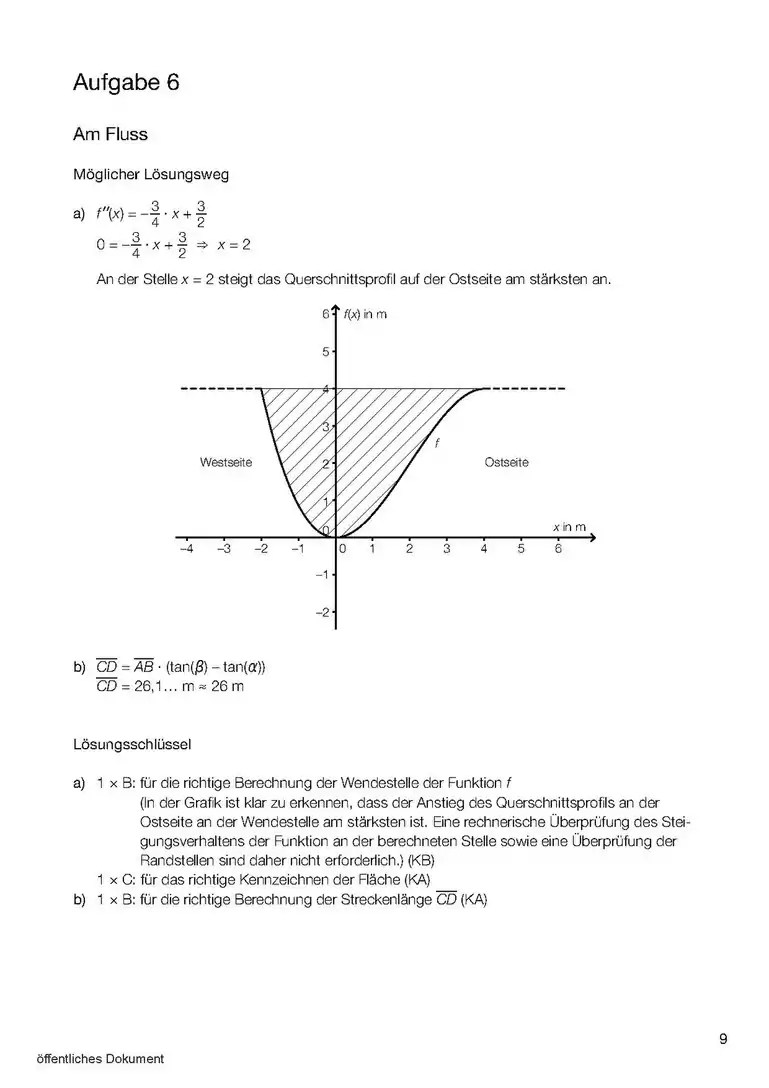
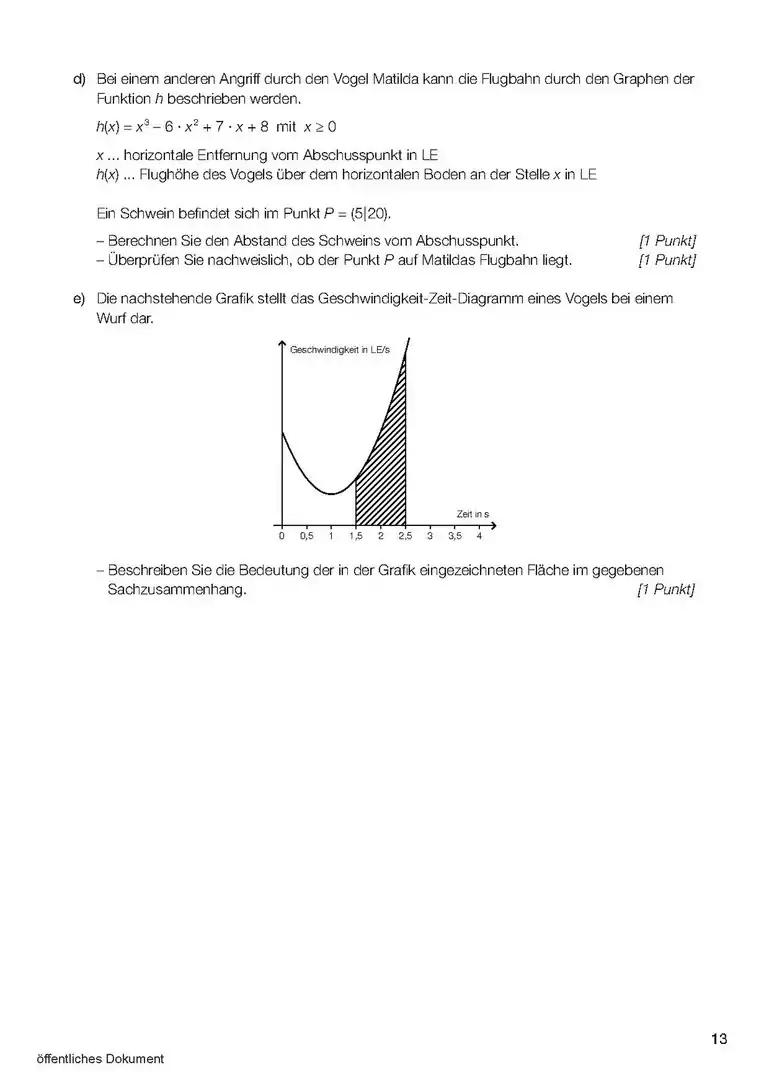
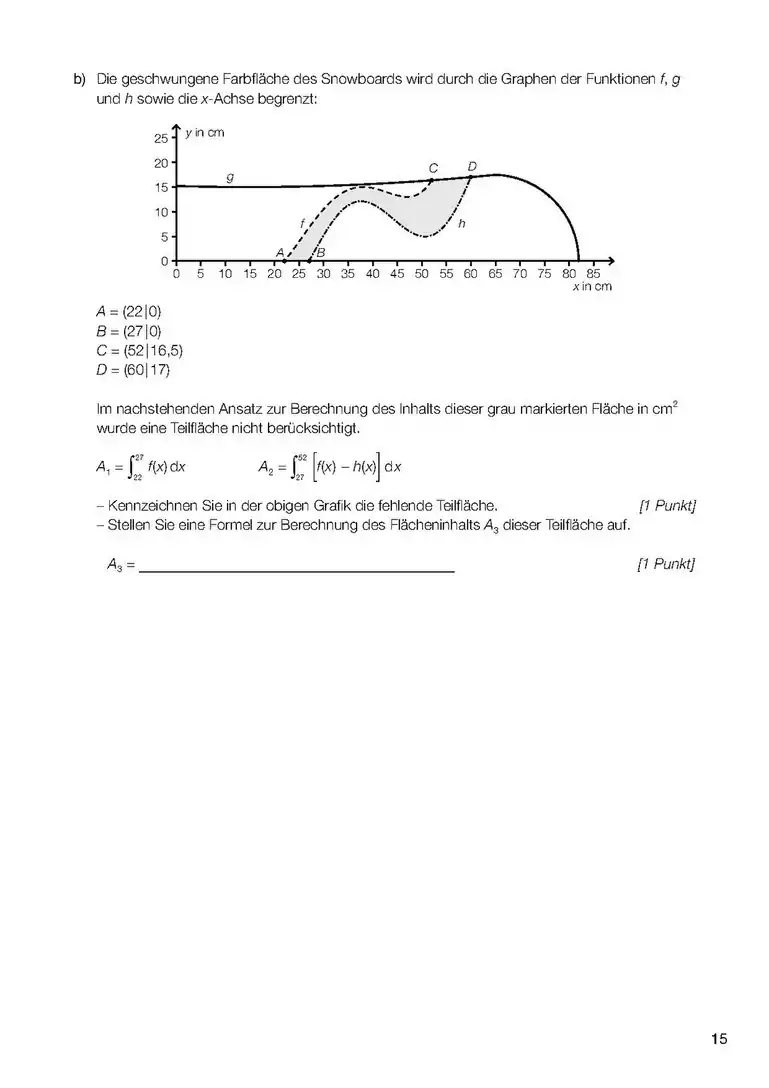
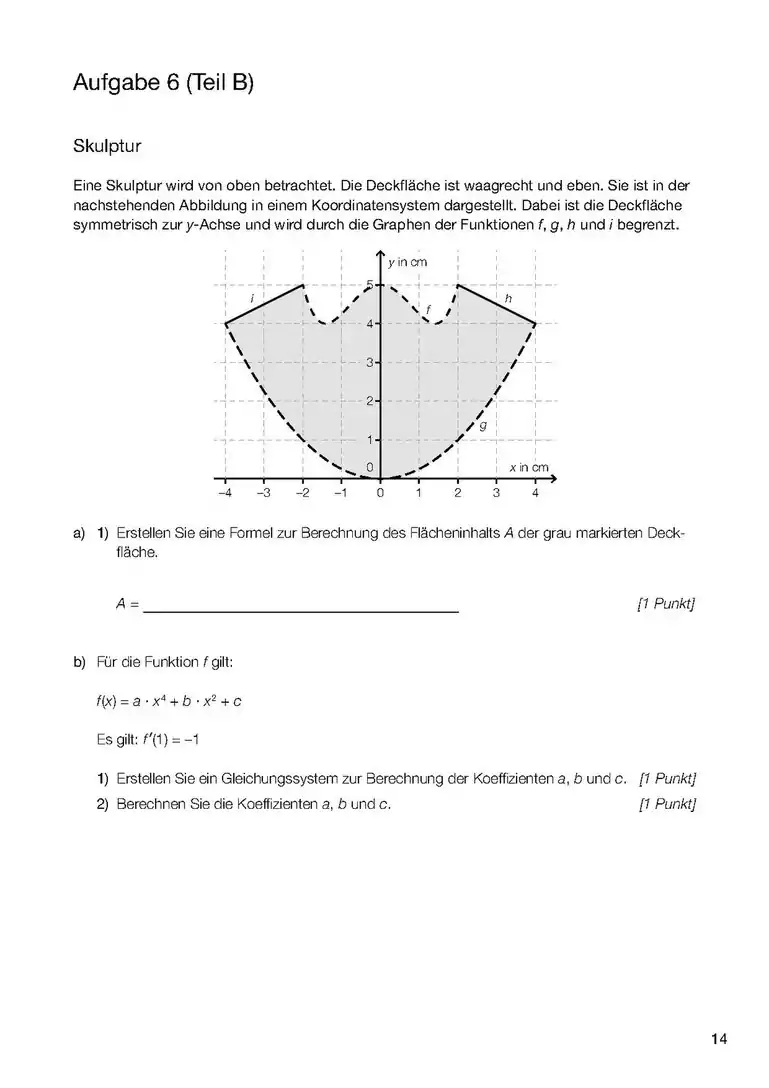
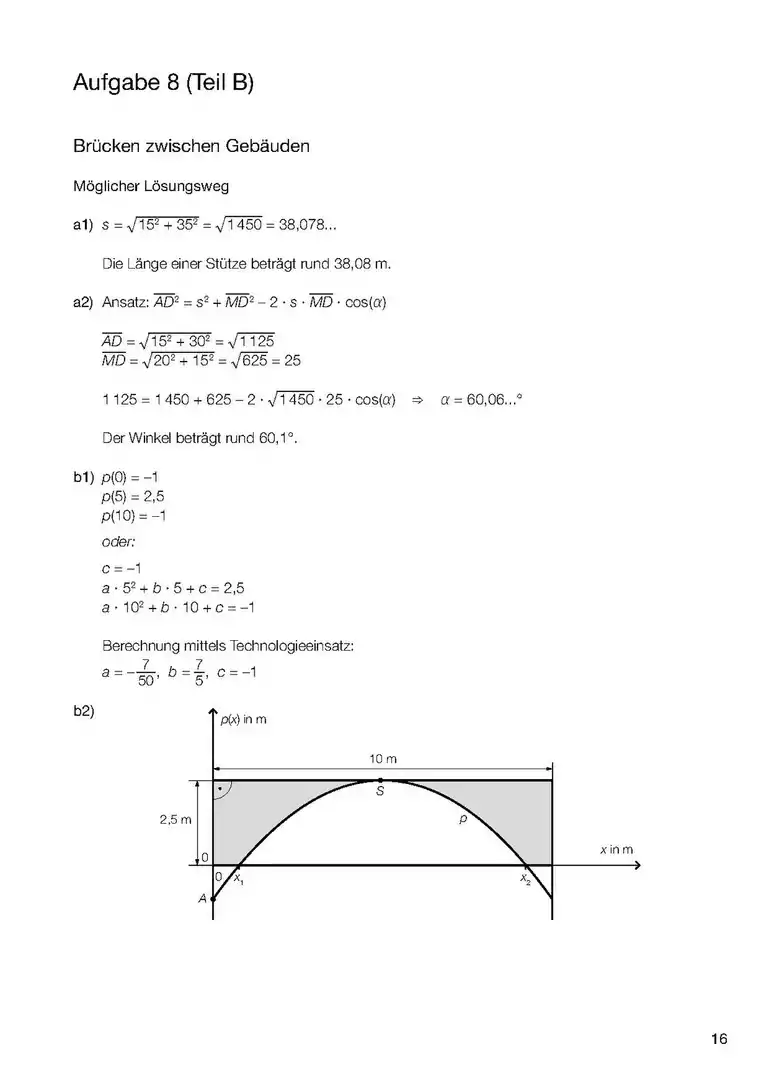
- Wenn es um das Integral einer Differenz geht, dann ist das Integral dieser Differenz die Fläche zwischen den beiden Funktionen (3. Bild). Aufpassen! Wenn ein Minus zwischen zwei Sachen da steht, dann haben wir schon zwei Funktionen. Dabei kann die eine nur eine Zahl sein, z.B. oder (4. und 5. Bild).
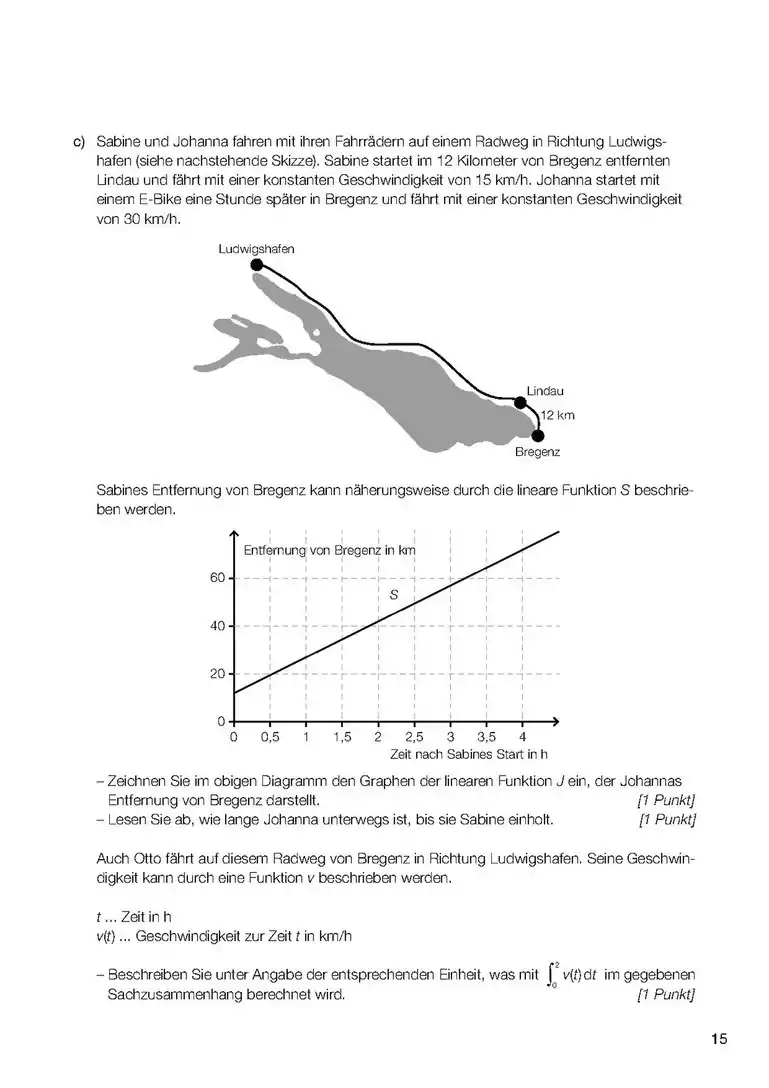
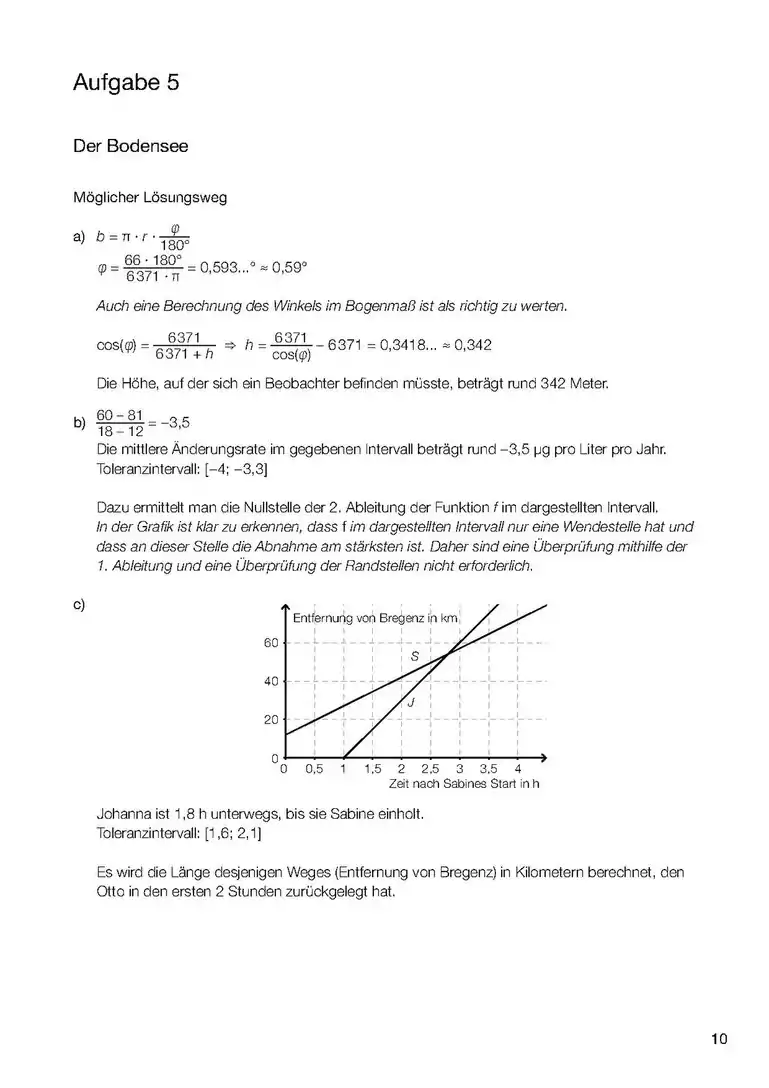
- Sind keine Grenzwerte angegeben, soll das sogenannte unbestimmte Integral berechnet werden (z.B. mit Geogebra), in diesem Fall steht auch eine Konstante immer dabei. Das Integral berechnet die Änderung der Größe, die durch die Fläche berechnet wird, z.B. zurückgelegte Strecke in einem v-t Diagramm (wie im Bild) und Geschwindigkeits-Änderung (und nicht die Geschwindigkeit an einem Zeitpunkt: dafür braucht man auch die Geschwindigkeit am Anfang) in einem a-t Diagramm (a: Beschleunigung).
| Maturaaufgaben nach Thema |
FARBINDEX
| Grün: Diese Aufgaben sollst du unbedingt lernen | |
| Lila: Diese Aufgaben sind mittlerer Schwierigkeit, lieber lernen | |
| Rot: Diese Aufgaben sind schwieriger | |
| Grün-Gelb: Diese Aufgaben sind ähnlich wie vorherigen grüne | |
| Rot-gelb (Orange): Diese Aufgaben sind ähnlich wie vorherigen rote | |
| Grau: Diese Aufgaben sind noch unsortiert |
|
This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.