Mathematrix: AT BRP/ Prüfungsbeispiele/ Exponentialfunktion

{\color {white}\mathbf {MATHE} \mu \alpha T\mathbb {R} ix}

DEINE FESTE BEGLEITERIN
FÜR DIE SCHULMATHEMATIK

EINFACH
VERSTÄNDLICH
AUFBAUEND

GRATIS!^*
UND SYMPATHISCH
JETZT STARTEN!

MIT MEHR ALS 200 THEORIE- UND AUFGABEN-ERKLÄRUNGSVIDEOS!

Mathe lernen ist wie Fahrradfahren lernen: Du kannst es dir stundenlang erklären lassen, du wirst nie fahren können, wenn du nicht selber zu fahren probierst.

LINKS

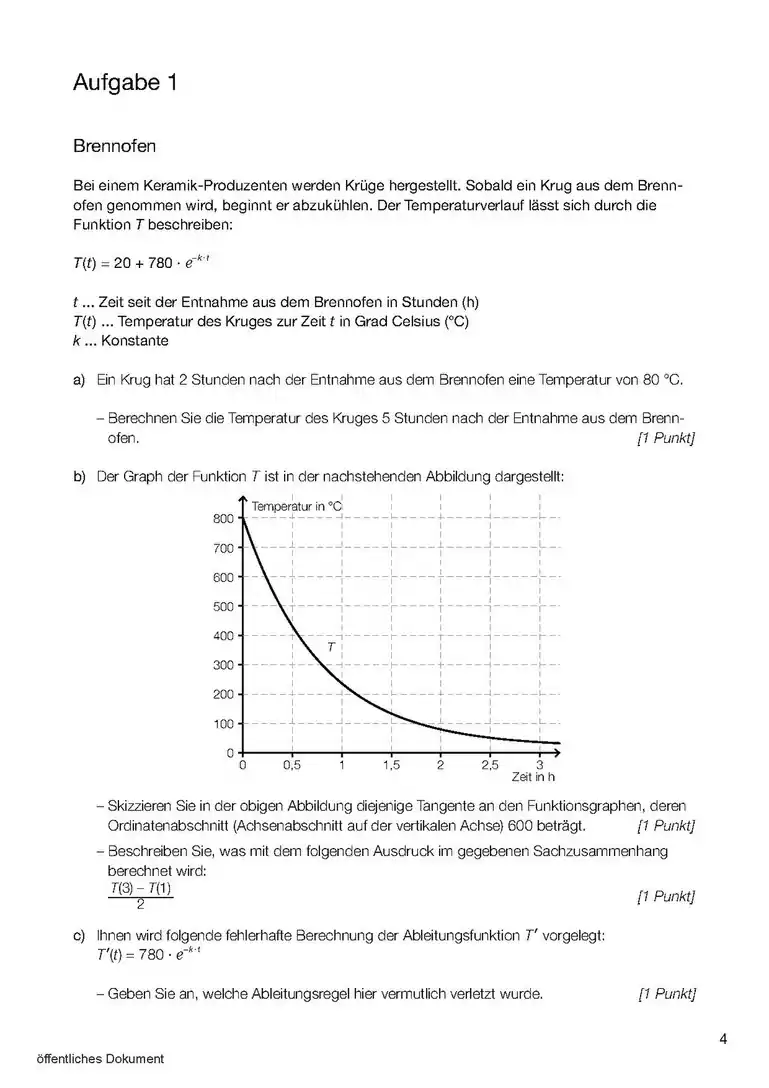
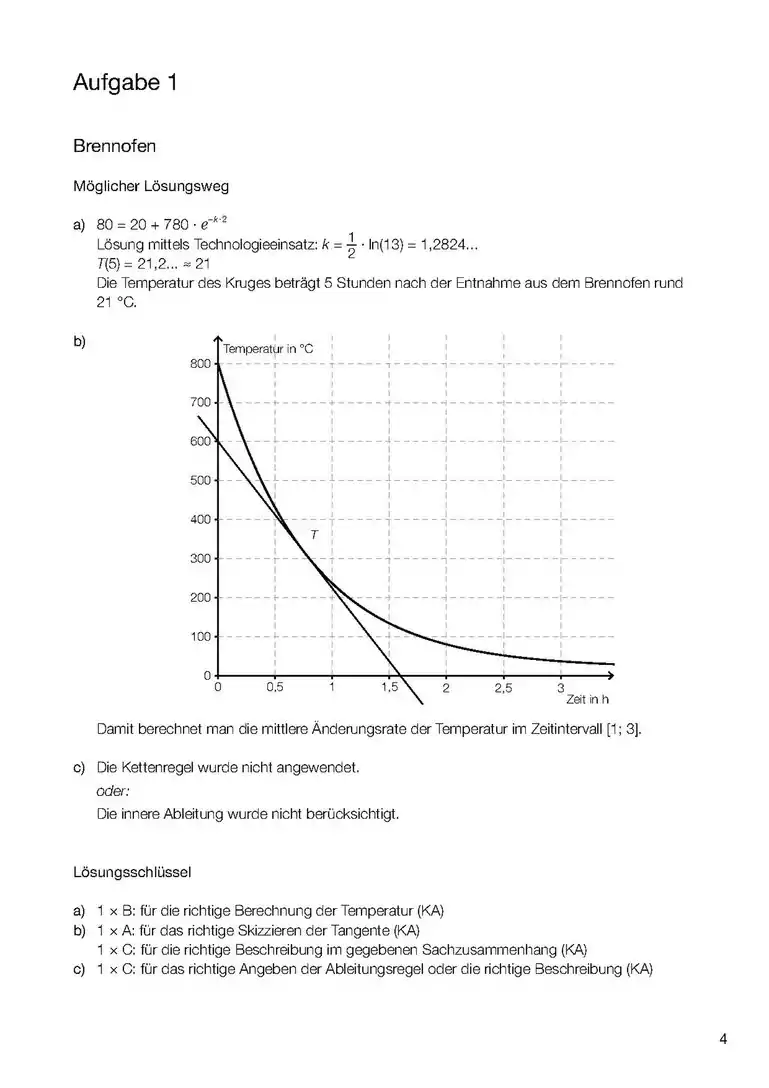
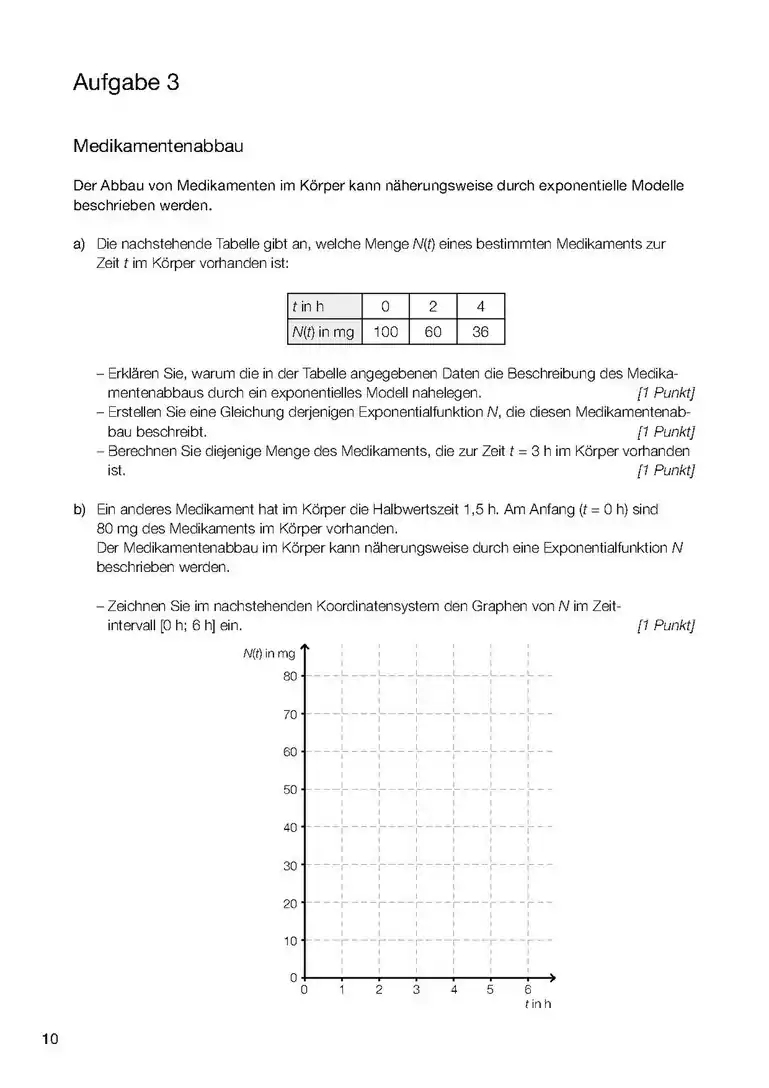
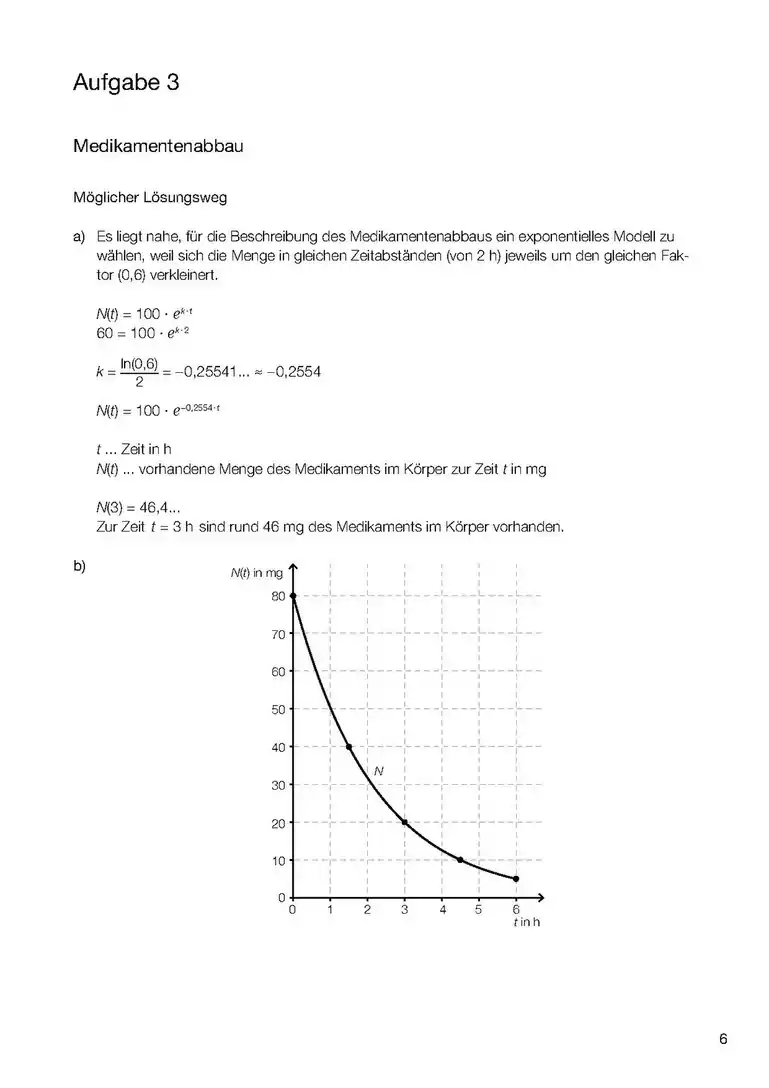
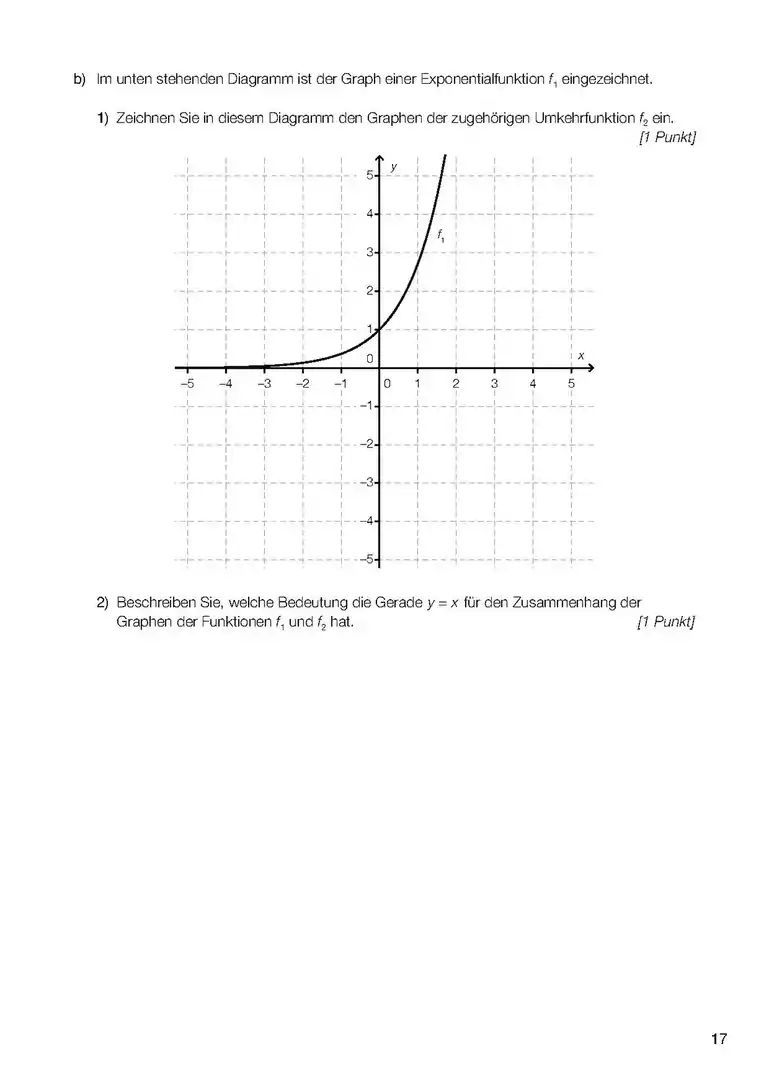
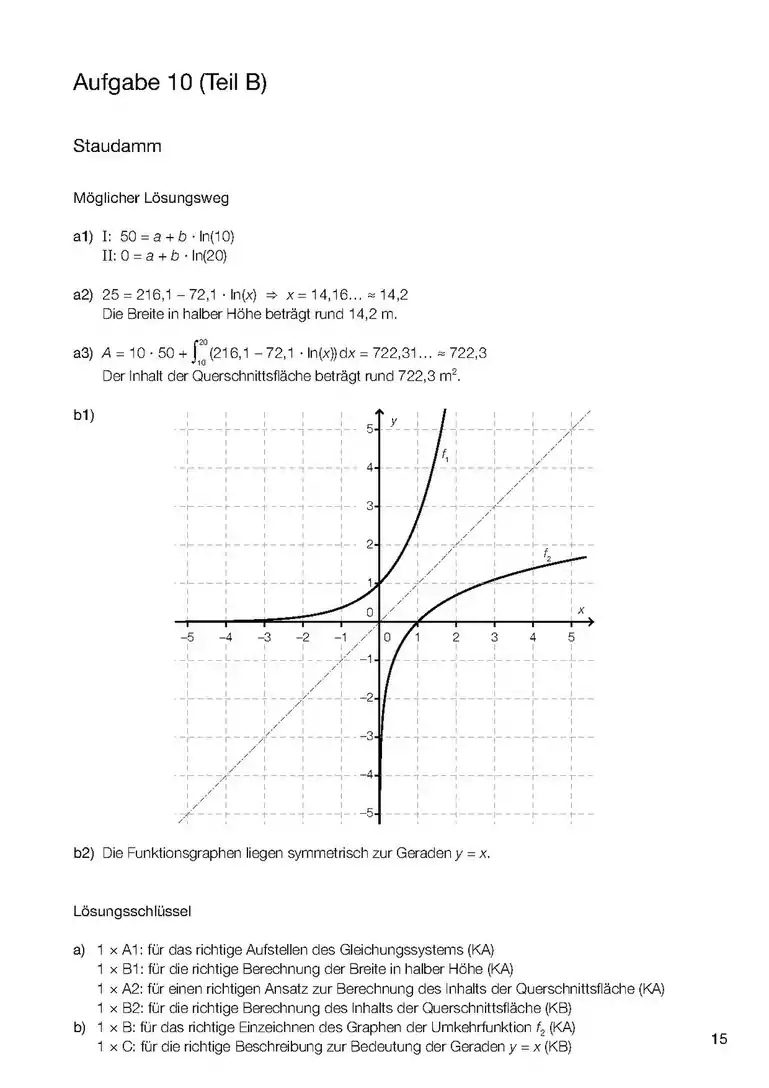
Theorie in Kürze (mit Geogebra)

$N(t)=N_{0}\cdot a^{t}$

N(t) ist die y-Achse (das y), t die x-Achse (das x). $N_{0}\$ ist der "Anfangswert", also der Wert der Funktion (y-Wert) da, wo x Null ist (y-Achsenabschnitt). Die Basis der Potenzzahl (das ist ein "Änderungsfaktor") kann man auch als "Prozentsatz" interpretieren, z.B. $N(t)=N_{0}\cdot 0{,}964^{t}$ bedeutet, dass bei jeder Änderung der x-Achse (z.B. t Zeit in Jahren) um 1 (z.B. jährlich) bleiben (0,964=) 96,4% des vorherigen Wertes, also 3,6% (100%−96,4%) weniger.

Extra Merkmal der Exponentialfunktion: Halbwertszeit: Nach der gleichen Änderung des x-Wertes wird der Wert der Funktion (y-Wert) immer halbiert. Im Bild: Am Anfang (also an der Stelle 0) ist der Wert der Funktion

N(0)=N_{0}\cdot a^{t}=8000\cdot a^{0}=8000\cdot 1=8000

, nach 3,5 auf der x-Achse (also an der Stelle 3,5) ist N(t) =N(3,5)=4000 (also die Hälfte), nach noch 3,5 auf der x-Achse (also an der Stelle 7) ist N(t) 2000 (also die Hälfte der Hälfte) usw.
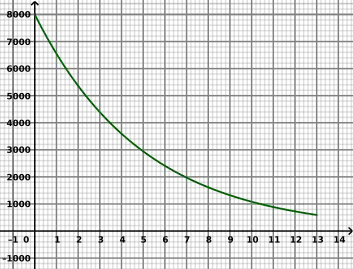
Die Halbwertszeit kann man berechnen, indem man am Wert Funktion die Hälfte des Anfangswerts einsetzt, z.B.

2350=4700\cdot 0{,}9^{t}

(2350 ist die Hälfte von 4700) oder

0{,}5=0{,}6^{t}

(hier "fehlt" der Anfangswert, er ist also 1, und die Hälfte von 1 ist ja 0,5). Entsprechend für eine "Verdoppelungszeit" oder ähnliches:

2=0{,}7^{t}

,

7{,}6=3{,}8\cdot 0{,}9^{t}

usw.

Noch dazu: die Exponentialfunktion hat keine "Nullstellen": sie kommt immer näher zur x-Achse aber trifft diese nie!

Maturaaufgaben
nach Thema

Einheiten und Zahlendarstellung

Formel erstellen anwenden umformen

Lineare Funktion und Regression

Exponentialfunktion

Kurvendiskussion Umkehraufgaben

Kurvendiskussion direkte Anwendung

Integrieren

Mittelwerte und Standardabweichung

Prozentrechnung

Boxplot

Binomialverteilung

Normalverteilung

Baumdiagramm

Mengenlehre

Folgen

Geometrie

Trigonometrie

Vektoren

Diagramme

FARBINDEX

$\$	Grün: Diese Aufgaben sollst du unbedingt lernen
$\$	Lila: Diese Aufgaben sind mittlerer Schwierigkeit, lieber lernen
$\$	Rot: Diese Aufgaben sind schwieriger
$\$	Grün-Gelb: Diese Aufgaben sind ähnlich wie vorherigen grüne
$\$	Rot-gelb (Orange): Diese Aufgaben sind ähnlich wie vorherigen rote
$\$	Grau: Diese Aufgaben sind noch unsortiert

$\$	Mai 2015 3A/B S.6 (hier klicken!)
	Lösung

$\$	Mai 2015 3C S.6 (hier klicken!)
	Lösung

$\$	Sep 2015 2Ai S.5 (hier klicken!)
	Lösung

$\$	Sep 2015 2Aii S.5 (hier klicken!)
	Lösung

$\$	Mai 2016 2B S.5 (hier klicken!)
	Lösung

$\$	Mai 2016 10Ai/ii S.15 (hier klicken!)
	Lösung

$\$	Mai 2016 10Aiii S.15 (hier klicken!)
	Lösung

$\$	Sep 2016 1A S.4 (hier klicken!)
	Lösung

$\$	Jan 2017 2A S.5 (hier klicken!)
	Lösung

$\$	Jan 2017 2B S.5 (hier klicken!)
	Lösung

$\$	Mai 2017 3Ai S.10 (hier klicken!)
	Lösung

$\$	Mai 2017 3Aii/iii/B S.10 (hier klicken!)
	Lösung

$\$	Mai 2017 3C/D S.10 (hier klicken!)
	Lösung

$\$	Mai 2017 4C S.13 (hier klicken!)
	Lösung

$\$	Mai 2017 6B S.17 (hier klicken!)
	Lösung

$\$	Sep 2017 4B S.10 (hier klicken!)
	Lösung

$\$	Sep 2017 7Aiv S.14 (hier klicken!)
	Lösung

$\$	Jan 2018 3C S.9 (hier klicken!)
	Lösung

$\$	Jan 2018 7Bii S.17 (hier klicken!)
	Lösung

$\$	Jan 2018 7Biii S.17 (hier klicken!)
	Lösung

$\$	Jan 2018 8Ai S.18 (hier klicken!)
	Lösung

$\$	Jan 2018 8Aii S.18 (hier klicken!)
	Lösung

$\$	Mai 2018 3Ci S.11 (hier klicken!)
	Lösung

$\$	Sep 2018 3A S.8 (hier klicken!)
	Lösung

$\$	Sep 2018 3B S.9 (hier klicken!)
	Lösung

$\$	Jan 2019 5A S.9 (hier klicken!)
	Lösung

$\$	Jan 2019 5B S.9 (hier klicken!)
	Lösung

$\$	Jan 2019 5C S.9 (hier klicken!)
	Lösung

$\$	Jan 2019 10bi S.17 (hier klicken!)
	Lösung

$\$	Mai 2019 2Ai S.5 (hier klicken!)
	Lösung

$\$	Mai 2019 2Aii S.5 (hier klicken!)
	Lösung

$\$	Mai 2019 5A S.9 (hier klicken!)
	Lösung

$\$	Mai 2019 5B S.9 (hier klicken!)
	Lösung

$\$	Sep 2019 5C S.13 (hier klicken!)
	Lösung

$\$	Sep 2019 9A S.20 (hier klicken!)
	Lösung

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.