Geschwindigkeit

Bei einer gleichförmigen Bewegung stimmt die Durchschnittsgeschwindigkeit mit der momentanen Geschwindigkeit überein.

Die Größe

${\displaystyle s(t):=s(t_{0})+\int _{t_{0}}^{t}|{\vec {v}}(t)|\,\mathrm {d} t}$

ist die zurückgelegte Strecke. Es gilt

${\displaystyle v(t)={\bigg |}{\frac {\mathrm {d} {\vec {r}}}{\mathrm {d} t}}{\bigg |}={\frac {\mathrm {d} s}{\mathrm {d} t}}.}$

Beschleunigung

Die Beschleunigung ist die zweite Ableitung des Ortes nach der Zeit:

${\displaystyle a_{x}(t)=x''(t).}$

Bei einer geradlinigen Bewegung gilt

${\displaystyle a(t)=v'(t).}$

Bei einer krummlinigen Bewegung zerfällt die Beschleunigung jedoch in zwei Komponenten:

die Tangentialbeschleunigung

${\displaystyle a_{\mathrm {tangential} }=v'(t)}$

und die Normalbeschleunigung

${\displaystyle a_{\mathrm {normal} }={\frac {v^{2}}{R}}.}$

Es gilt

${\displaystyle {\vec {a}}=a_{\mathrm {tangential} }{\hat {t}}+a_{\mathrm {normal} }{\hat {n}}}$

und

${\displaystyle a={\sqrt {a_{\mathrm {tangential} }^{2}+a_{\mathrm {normal} }^{2}}}.}$

Hierbei ist

• ${\displaystyle R}$ der Radius des Krümmungskreises am Ort ${\displaystyle {\vec {r}}(t)}$,
• ${\displaystyle {\hat {t}}}$ der Tangenteneinheitsvektor am Ort ${\displaystyle {\vec {r}}(t)}$,
• ${\displaystyle {\hat {n}}}$ der Normaleneinheitsvektor am Ort ${\displaystyle {\vec {r}}(t)}$.

Impuls

Impulsvektor und Geschwindigkeitsvektor zeigen in die gleiche Richtung.

Für die Komponenten gilt:

p_x = mv_x,

p_y = mv_y,

p_z = mv_z.

Für die Beträge gilt:

p = mv.

Kraft

Für eine zeitlich konstante Masse m gilt:

${\displaystyle F_{x}=ma_{x}.}$

Für eine zeitlich konstante Masse m gilt:

${\displaystyle {\vec {F}}=m{\vec {a}}.}$

Für die betragsmäßige Kraft gilt dann

${\displaystyle F=ma}$

mit ${\displaystyle F:=|{\vec {F}}|}$ und ${\displaystyle a:=|{\vec {a}}|}$.

Für eine zeitlich veränderliche Masse ergibt sich jedoch

${\displaystyle {\vec {F}}={\frac {\mathrm {d} m}{\mathrm {d} t}}\,{\vec {v}}+m{\vec {a}}.}$

Arbeit

Für eine konstante Kraft F gilt

${\displaystyle W=F\Delta x=F\cdot (x_{2}-x_{1}).}$

Für eine konstante Kraft ${\displaystyle {\vec {F}}}$ gilt

${\displaystyle W=\langle {\vec {F}},\Delta {\vec {r}}\rangle =\langle {\vec {F}},{\vec {r}}(t_{2})-{\vec {r}}(t_{1})\rangle .}$

Die Anheftung der selben konstanten Kraft an jeden Ort ist ein Potentialfeld, da die Arbeit unabhängig vom gewählten Weg von ${\displaystyle {\vec {r}}_{1}={\vec {r}}(t_{1})}$ nach ${\displaystyle {\vec {r}}_{2}={\vec {r}}(t_{2})}$ ist. Geht man vom direkten Weg aus und meint mit

${\displaystyle s:=|{\vec {r}}_{2}-{\vec {r}}_{1}|}$

den Abstand, das ist die kürzeste Streckenlänge, dann ergibt sich die Formel

${\displaystyle W=F\cdot s\cdot \cos \varphi }$

mit ${\displaystyle F:=|{\vec {F}}|}$ und ${\displaystyle \varphi$ :=\angle ({\vec {F}},\Delta {\vec {r}}).}

Beschleunigungsarbeit
Wird eine Punktmasse m von einer Geschwindigkeit v₀ auf eine Geschwindigkeit v beschleunigt, dann muss gegen die Trägheit der Masse gearbeitet werden. Die Beschleunigungsarbeit beträgt

${\displaystyle W_{B}={\frac {1}{2}}mv^{2}-{\frac {1}{2}}mv_{0}^{2}.}$

Die Beschleunigungsarbeit ist neben der Masse und der Anfangsgeschwindigkeit nur von der erreichten Endgeschwindigkeit abhängig. Ob die Punktmasse gleichförmig beschleunigt wurde oder nicht, ist dabei unwesentlich.

Hubarbeit
Für einen kleinen Höhenunterschied darf die Fallbeschleunigung g als näherungsweise konstant angenommen werden. Demnach ist auch die Kraft

${\displaystyle F_{g}=mg}$

näherungsweise konstant. Um eine Punktmasse m um eine Höhe h zu heben, muss nun die Hubarbeit

${\displaystyle W_{H}=F_{g}\,h=m\,g\,h.}$

aufgebracht werden.

Spannarbeit
Bei einer idealen Feder wirkt der Auslenkung x die Kraft

${\displaystyle F=kx}$

entgegen, wobei k die Federkonstante ist. Bei der Auslenkung der Feder von x₀ bis x muss die Spannarbeit

${\displaystyle W_{\text{Spann}}={\frac {1}{2}}kx^{2}-{\frac {1}{2}}kx_{0}^{2}}$

aufgebracht werden.

Energie

Kinetische Energie

Kinetische Energie einer Masse ${\displaystyle m}$ mit der Geschwindigkeit ${\displaystyle v}$:

${\displaystyle E_{\mathrm {kin} }={\frac {1}{2}}\,m\cdot v^{2}\quad \mathrm {bei} \ v\ll c}$   mit c = Lichtgeschwindigkeit.

Kartesische Koordinaten	${\displaystyle E_{\mathrm {kin} }={\tfrac {1}{2}}m({\dot {x}}^{2}+{\dot {y}}^{2}+{\dot {z}}^{2})}$
Polarkoordinaten	${\displaystyle E_{\mathrm {kin} }={\tfrac {1}{2}}m({\dot {r}}^{2}+r^{2}{\dot {\varphi }}^{2})}$
Zylinderkoordinaten	${\displaystyle E_{\mathrm {kin} }={\tfrac {1}{2}}m({\dot {r}}^{2}+r^{2}{\dot {\varphi }}^{2}+{\dot {z}}^{2})}$
Kugelkoordinaten	${\displaystyle E_{\mathrm {kin} }={\tfrac {1}{2}}m({\dot {r}}^{2}+r^{2}{\dot {\theta }}^{2}+r^{2}{\dot {\varphi }}^{2}\sin \theta )}$
Allgemein	${\displaystyle E_{\mathrm {kin} }={\tfrac {1}{2}}m|{\vec {v}}|^{2}}$

Potentielle Energie

Potentielle Energie an der Erdoberfläche:

${\displaystyle E_{\mathrm {pot} }=m\cdot g\cdot h}$

mit:

• ${\displaystyle g\colon }$ Gravitationsbeschleunigung
• ${\displaystyle h\colon }$ Hubhöhe.

Achtung: Dies ist keine allgemeine Formel für die potentielle Energie, sondern nur ein Spezialfall in der Nähe der Erdoberfläche. Bei anderen Problemen sieht die potentielle Energie anders aus – zum Beispiel bei Molekülen, einer Feder, im Potential einer Ladung oder im Gravitationspotential.

Spannenergie

Spannenergie einer Feder:

${\displaystyle E_{\mathrm {Spann} }=E_{pot}={\frac {1}{2}}\,D\cdot s^{2}}$

mit:

• ${\displaystyle D}$: Federkonstante,
• ${\displaystyle s\colon }$: Auslenkung der Feder aus der Ruhelage.

Spannenergie einer Drehfeder:

${\displaystyle E_{\mathrm {Spann} }=E_{pot}={\frac {1}{2}}\,D\cdot \varphi ^{2}}$

mit:

• ${\displaystyle D\colon }$: Direktionsmoment,
• ${\displaystyle \varphi \colon }$: Auslenkungswinkel der Feder aus der Ruhelage.

Leistung

Die Leistung ${\displaystyle P}$ ist der Quotient aus verrichteter Arbeit ${\displaystyle \Delta W}$ oder dafür aufgewendeter Energie ${\displaystyle \Delta E}$ und der dazu benötigten Zeit ${\displaystyle \Delta t}$:

${\displaystyle P={\frac {\Delta E}{\Delta t}}={\frac {\Delta W}{\Delta t}}}$

oder:

${\displaystyle P={\dot {W}}={\vec {F}}\cdot {\frac {\mathrm {d} {\vec {s}}}{\mathrm {d} t}}={\vec {F}}\cdot {\vec {v}}.}$

In einem Zeitintervall der Länge ${\displaystyle T=\left[t_{1},t_{2}\right]}$ verrichtete mittlere Leistung ${\displaystyle {\overline {P}}:}$

${\displaystyle {\overline {P}}={\frac {1}{T}}\int _{t_{1}}^{t_{2}}P(t)\mathrm {d} t.}$

Diese Angabe hat insbesondere Bedeutung, wenn ${\displaystyle P(t)}$ sich periodisch ändert und ${\displaystyle T}$ die Periodendauer ist.

Wirkungsgrad

${\displaystyle \eta ={\frac {W_{abgegeben}}{W_{zugef{\ddot {u}}hrt}}}\cdot 100\%={\frac {E_{abgegeben}}{E_{zugef{\ddot {u}}hrt}}}\cdot 100\%={\frac {P_{abgegeben}}{P_{zugef{\ddot {u}}hrt}}}\cdot 100\%<1.}$

Gesamtwirkungsgrad

Bei der Verkettung von Energie-umformenden Einrichtungen ist der Gesamtwirkungsgrad das Produkt der einzelnen Wirkungsgrade:

${\displaystyle \eta _{\mathrm {ges} }=\eta _{1}\cdot \eta _{2}\cdot \ldots \cdot \eta _{n}.}$

Gleichförmige geradlinige Bewegung

Weg	Geschwindigkeit	Beschleunigung
${\displaystyle s=v\cdot (t-t_{0})+s_{0}}$	${\displaystyle v=v_{0}={\frac {s-s_{0}}{t-t_{0}}}}$	${\displaystyle a=0}$

Gleichmäßig beschleunigte geradlinige Bewegung

Weg	Geschwindigkeit	Beschleunigung
${\displaystyle s={\frac {a}{2}}\cdot (t-t_{0})^{2}+v_{0}\cdot (t-t_{0})+s_{0}}$	${\displaystyle v=a\cdot (t-t_{0})+v_{0}}$	${\displaystyle a=a_{0}={\frac {v-v_{0}}{t-t_{0}}}}$
${\displaystyle s={\frac {v^{2}-v_{0}^{2}}{2a}}+s_{0}}$	${\displaystyle v={\sqrt {v_{0}^{2}+2a\cdot (s-s_{0})}}}$	${\displaystyle a={\frac {v^{2}-v_{0}^{2}}{2(s-s_{0})}}}$

Durchschnittsgeschwindigkeit

${\displaystyle {\frac {s-s_{0}}{t-t_{0}}}={\frac {1}{2}}(v+v_{0}).}$

Allgemeine geradlinige Bewegung

Weg	Geschwindigkeit	Beschleunigung
${\displaystyle s=\int _{t_{0}}^{t}v\,\mathrm {d} t+s_{0}}$	${\displaystyle v={\frac {\mathrm {d} s}{\mathrm {d} t}}=\int _{t_{0}}^{t}a\,\mathrm {d} t+v_{0}}$	${\displaystyle a={\frac {\mathrm {d} v}{\mathrm {d} t}}}$

Gleichförmige Kreisbewegung

${\displaystyle {\vec {r}}(t)}$	Ortsvektor zum Zeitpunkt t
${\displaystyle r}$	Radius
${\displaystyle \omega }$	Winkelgeschwindigkeit
${\displaystyle \varphi (t)}$	Winkel zum Zeitpunkt t
${\displaystyle \varphi _{0}}$	Anfangswinkel
${\displaystyle T}$	Umlaufzeit
${\displaystyle n}$	Drehzahl

Für die Winkelgeschwindigkeit gilt:

${\displaystyle \omega ={\frac {\Delta \varphi }{\Delta t}}={\frac {v}{r}}={\frac {2\pi }{T}}=2\pi n.}$

Für die Beschleunigung gilt:

${\displaystyle {\vec {a}}=-\omega ^{2}{\vec {r}}.}$

Die Beschleunigung stimmt mit der Zentripetalbeschleunigung überein:

${\displaystyle {\vec {a}}={\vec {a}}_{\mathrm {zp} }=-{\vec {a}}_{\mathrm {zf} }.}$

Betragsmäßige Gleichungen:

${\displaystyle v=\omega r,}$

${\displaystyle a_{\mathrm {zp} }=\omega ^{2}r.}$

Der Geschwindigkeitsvektor steht senkrecht zum Ortsvektor:

${\displaystyle \langle {\vec {v}},{\vec {r}}\rangle =0.}$

Der Beschleunigungsvektor steht senkrecht zum Geschwindigkeitsvektor:

${\displaystyle \langle {\vec {a}},{\vec {v}}\rangle =0.}$

Es gibt keine messbare Winkelbeschleunigung:

${\displaystyle \alpha =0.}$

Gleichmäßig beschleunigte Kreisbewegung

Es gilt

${\displaystyle \omega =\alpha t+\omega _{0},}$

${\displaystyle \alpha ={\frac {\Delta \omega }{\Delta t}}}$ = konstant,

${\displaystyle v=\omega r}$,

${\displaystyle a=r{\sqrt {\alpha ^{2}+\omega ^{4}}}}$.

Für die Tangential- und die Zentripetalbeschleunigung gilt:

${\displaystyle a_{\mathrm {tan} }=\alpha r}$,

${\displaystyle a_{\mathrm {zp} }=\omega ^{2}r}$.

Allgemeine Kreisbewegung

Es gilt:

${\displaystyle v=\omega r}$,

${\displaystyle a=r{\sqrt {\alpha ^{2}+\omega ^{4}}}}$.

Für die Tangential- und die Zentripetalbeschleunigung gilt:

${\displaystyle a_{\mathrm {tan} }=\alpha r}$,

${\displaystyle a_{\mathrm {zp} }=\omega ^{2}r}$,

${\displaystyle a^{2}=a_{\mathrm {tan} }^{2}+a_{\mathrm {zp} }^{2}.}$

Die folgenden vektoriellen Beziehungen sind gültig:

${\displaystyle {\vec {v}}=\omega R({\tfrac {\pi }{2}}){\vec {r}}}$,

${\displaystyle {\vec {a}}_{\mathrm {tan} }=\alpha R({\tfrac {\pi }{2}}){\vec {r}}}$,

${\displaystyle {\vec {a}}_{\mathrm {zp} }=-\omega ^{2}{\vec {r}}}$,

${\displaystyle {\vec {a}}={\vec {a}}_{\mathrm {tan} }+{\vec {a}}_{\mathrm {zp} }}$.

Mit

${\displaystyle R({\tfrac {\pi }{2}})={\begin{bmatrix}0&-1\\1&0\end{bmatrix}}}$

ist die Rotationsmatrix gemeint, die einen Vektor um 90° gegen den Uhrzeigersinn dreht.

Zentripetalkraft

Jeder Massepunkt der um eine feste Achse rotiert bewegt sich stets tangential. Um das Entfernen in diese Richtung zu verhindern bedarf es der Zentripetalkraft, welche Radial wirkt, also senkrecht zur Bewegungsrichtung, und so den Massepunkt auf eine Kreisbahn um die Achse zwingt. Die Zentripetalkraft ist inertial und unterscheidet sich somit von der "Schein" -Zentrifugalkraft.

Für die Zentripetalkraft gilt:

${\displaystyle {\vec {F}}_{\mathrm {zp} }:=m\cdot {\vec {a}}_{\mathrm {zp} }=-m\cdot \omega ^{2}\cdot {\vec {r}},}$

${\displaystyle F_{\mathrm {zp} }:=|{\vec {F}}_{\mathrm {zp} }|=m\cdot \omega ^{2}\cdot r.}$

Zentrifugalkraft

Die Zentrifugalkraft ist im Gegensatz zur Zentripedalkraft eine Scheinkraft, da sie nicht im inertialen äußeren Bezugssystem existiert sondern nur im relativen rotierenden System anscheinend in Erscheinung tritt. Wird ein um eine Achse rotierender Körper losgelassen, bewegt er sich im rotierenden Bezugssystem im ersten Moment Radial fort.

Für die Zentrifugalkraft gilt:

${\displaystyle {\vec {F}}_{\mathrm {zf} }=-m{\vec {\omega }}\times ({\vec {\omega }}\times r).}$

Dabei ist ${\displaystyle m}$ die Masse des Körpers, ${\displaystyle {\vec {\omega }}}$ die Winkelgeschwindigkeit des Bezugssystems und ${\displaystyle {\vec {r}}}$ der Ortsvektor vom Ursprung des Bezugssystems.

Für den Spezialfall dass der Körper im rotierenden Bezugssystem ruht, ist die Zentrifugalkraft der Trägheitswiderstand in Bezug auf die Zentripetalkraft:

${\displaystyle {\vec {F}}_{\mathrm {zf} }=-{\vec {F}}_{\mathrm {zp} }.}$

Dieser Trägheitswiderstand ist auch im Inertialsystem definiert.

Freier Fall ohne und mit Luftwiderstand

Die folgenden Formeln beschreiben die Bewegung bei konstanter Beschleunigung. Dies trifft zum Beispiel näherungsweise zu, wenn man Objekte in der Nähe der Erdoberfläche fallenläßt, entsprechend mit anderer Beschleunigung natürlich auch in der Nähe anderer großer Objekte wie Planeten, Monde, Sonnen etc.

${\displaystyle g}$: Erdbeschleunigung [m/s²] (~9.8 m/s² in der Nähe der Erdoberfläche)

${\displaystyle h}$: Fallhöhe [m]

ohne Reibung

Das ist der eigentliche freie Fall im Vakuum.

${\displaystyle v=g\cdot t={\sqrt {2\cdot g\cdot h}}}$

${\displaystyle t={\sqrt {\frac {2\cdot h}{g}}}}$

${\displaystyle s={\frac {1}{2}}\cdot g\cdot t^{2}}$

mit Reibung

Reibung an sich ist ein recht komplexer Vorgang, bei dem Bewegungsenergie verloren geht, bezogen auf den freien Fall wird dies primär dadurch bewirkt, dass etwas durch die Luft fällt oder durch Wasser als Flüssigkeit. Je nach Geschwindigkeit und Medium, durch welches die Bewegung führt, ist hat die Reibung andere Effekte.

Fall 1: Newton-Reibung

Dabei wird die Reibungskraft proportional zum Quadrat des Betrages der Geschwindigkeit relativ zum Medium angenommen. Das tritt besonders bei hohen Geschwindigkeiten oder dichten Medien auf. Im Falle von Gasen erzeugt das bewegte Objekt im Medium dabei meist Turbulenzen, die einen hohen Energieverlust bedeuten. Bei Medien geringer Dichte oder kleinen Geschwindigkeiten wird dabei die Reibung eher zu klein abgeschätzt.

Momentanhöhe:

${\displaystyle h(t)=H-{\frac {m}{\alpha }}\ln \left[\cosh \left({\sqrt {\frac {\alpha g}{m}}}\cdot t\right)\right]}$

${\displaystyle v(t)=-{\sqrt {\frac {mg}{\alpha }}}\tanh \left({\sqrt {\frac {\alpha g}{m}}}\cdot t\right)}$

${\displaystyle a(t)=-{\frac {g}{\cosh ^{2}\left({\sqrt {\frac {\alpha g}{m}}}\cdot t\right)}}}$

Grenzgeschwindigkeit:

${\displaystyle v_{\mathrm {g} }=-{\sqrt {\frac {mg}{\alpha }}}}$

Im Newton-Fall ist ${\displaystyle \alpha ={\tfrac {1}{2}}\cdot c_{\mathrm {w} }\,\rho \,A}$, mit

${\displaystyle H}$: Anfangshöhe

${\displaystyle c_{\mathrm {w} }}$: Strömungswiderstandskoeffizient

${\displaystyle \rho }$: Luftdichte

${\displaystyle A}$: Stirnfläche des fallenden Körpers

Fall 2: Stokes-Reibung

Bei Medien geringer Dichte oder kleinen Geschwindigkeiten wird dabei die Reibungskraft proportional zum Betrag der Geschwindigkeit abgeschätzt. Bei hoher Dichte oder hoher Geschwindigkeit wird damit die Reibung als zu klein abgeschätzt.

${\displaystyle h(t)=H+{\frac {m}{\alpha }}g\left[{\frac {m}{\alpha }}\left(1-e^{-(\alpha /m)t}\right)-t\right]}$

${\displaystyle v(t)={\frac {m}{\alpha }}g\left(e^{-(\alpha /m)t}-1\right)}$

${\displaystyle a(t)=-g\,e^{-{\frac {\alpha }{m}}t}}$

${\displaystyle v_{g}=-{\frac {m}{\alpha }}g}$

Senkrechter Wurf ohne Luftwiderstand

Ort-Zeit-Gesetz	${\displaystyle y=v_{0}t-{\frac {g}{2}}t^{2}+y_{0}}$
Geschwindigkeit-Zeit-Gesetz	${\displaystyle v=v_{0}-gt}$
Ort-Geschwindigkeit-Gesetz	${\displaystyle y={\frac {v_{0}^{2}-v^{2}}{2g}}+y_{0}}$
Steigzeit	${\displaystyle t_{u}={\frac {v_{0}}{g}}}$
Gipfelpunkt	${\displaystyle y_{u}={\frac {v_{0}^{2}}{2g}}+y_{0}}$

${\displaystyle v_{0}>0}$	Wurf nach oben
${\displaystyle v_{0}<0}$	Wurf nach unten

Waagerechter Wurf ohne Luftwiderstand

	x	y
Ort-Zeit-Gesetz	${\displaystyle x=x_{0}+v_{0}t}$	${\displaystyle y=y_{0}-{\frac {g}{2}}t^{2}}$
Geschwindigkeit-Zeit-Gesetz	${\displaystyle v_{x}=v_{0}}$	${\displaystyle v_{y}=-gt}$
	${\displaystyle |{\vec {v}}|={\sqrt {v_{0}^{2}+(gt)^{2}}}}$
Wurfparabel	${\displaystyle y=y_{0}-{\frac {g}{2v_{0}^{2}}}(x-x_{0})^{2}}$

Schräger Wurf ohne Luftwiderstand

	x	y
Ort-Zeit-Gesetz	${\displaystyle x=v_{x}(0)\,t}$	${\displaystyle y=v_{y}(0)\,t-{\frac {g}{2}}t^{2}}$
Geschwindigkeit-Zeit-Gesetz	${\displaystyle v_{x}=v_{x}(0)}$	${\displaystyle v_{y}=v_{y}(0)-gt}$
Startgeschwindigkeit	${\displaystyle v_{x}(0)=v_{0}\cos \alpha }$	${\displaystyle v_{y}(0)=v_{0}\sin \alpha }$
	${\displaystyle v_{0}:=|{\vec {v}}_{0}|={\sqrt {v_{x}(0)^{2}+v_{y}(0)^{2}}}}$

1. Newtonsches Axiom

Ein kräftefreier Körper bleibt in Ruhe oder bewegt sich geradlinig mit konstanter Geschwindigkeit.

2. Newtonsches Axiom

Eine auf einen Körper wirkende Kraft ${\displaystyle {\vec {F}}}$ ändert dessen Impuls: Die Impulsänderung pro Zeit ist gleich der auf den Körper wirkenden Kraft.

${\displaystyle {\vec {F}}={\frac {\mathrm {d} }{\mathrm {d} t}}\;{\vec {p}}}$

Ist die Masse ${\displaystyle m}$ während der Impulsänderung konstant, ergibt sich die bekanntere Formel:

${\displaystyle {\vec {F}}=m{\frac {\mathrm {d} }{\mathrm {d} t}}{\vec {v}}=m\cdot {\vec {a}}}$

3. Newtonsches Axiom

Kraft gleich Gegenkraft: Eine Kraft von Körper A auf Körper B geht immer mit einer gleich großen, aber entgegen gerichteten Kraft von Körper B auf Körper A einher.

${\displaystyle {\vec {F}}_{A\to B}=-{\vec {F}}_{B\to A}}$

Hebelgesetz

Drehmoment = Kraft · Länge des Hebelarmes:

${\displaystyle M=F\cdot s.}$

Einheit: ${\displaystyle \mathrm {N} \cdot \mathrm {m} }$ = Newton · Meter

Im Gleichgewicht gilt:

${\displaystyle M_{1}=M_{2}.}$

Rechts drehendes Moment = Links drehendes Moment:

${\displaystyle F_{1}\cdot s_{1}=F_{2}\cdot s_{2}.}$

Flaschenzug

Besteht der Flaschenzug aus n Rollen, so verteilt sich die Last ebenfalls auf n Seile. Im Falle des Gleichgewichts gilt:

Kraft = Last / Anzahl der Seile:

${\displaystyle F_{1}={\frac {F_{2}}{n}}}$,

wobei ${\displaystyle F_{1}}$ die aufzuwendende Kraft und ${\displaystyle F_{2}}$ die Last bedeutet.

Schiefe Ebene

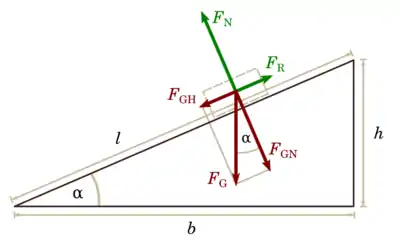
Nomenklatur
${\displaystyle {\vec {F}}_{\mathrm {G} }}$	Gewichtskraft
${\displaystyle {\vec {F}}_{\mathrm {GN} }}$	Normalkomponente der Gewichtskraft
${\displaystyle {\vec {F}}_{\mathrm {GH} }}$	Hangabtriebskomponente der Gewichtskraft
${\displaystyle {\vec {F}}_{\mathrm {N} }}$	Normalkraft
${\displaystyle {\vec {F}}_{\mathrm {R} }}$	Haftreibungskraft
${\displaystyle \mu _{\mathrm {H} }}$	Haftreibungskoeffizient
${\displaystyle \alpha }$	Neigungswinkel
${\displaystyle l}$	Länge
${\displaystyle h}$	Höhe
${\displaystyle b}$	Basis

${\displaystyle b=l\cos \alpha }$	${\displaystyle F_{\mathrm {GN} }=F_{\mathrm {G} }\cos \alpha }$	${\displaystyle F_{\mathrm {N} }=F_{\mathrm {GN} }}$
${\displaystyle h=l\sin \alpha }$	${\displaystyle F_{\mathrm {GH} }=F_{\mathrm {G} }\sin \alpha }$	${\displaystyle F_{\mathrm {R} }=F_{\mathrm {GH} }}$

Bedingung für die Ruhe eines haftenden Körpers:

${\displaystyle F_{\mathrm {R} }\leq \mu _{\mathrm {H} }\cdot F_{\mathrm {N} }\quad {\text{bzw.}}\quad \tan \alpha \leq \mu _{\mathrm {H} }.}$

Reibung

Reibungskraft = Reibungszahl · Normalkraft:

${\displaystyle F_{R}=\mu \cdot F_{N}.}$

Trockene Reibung (Gleitreibung):

${\displaystyle {\vec {F}}_{\mathrm {RT} }=-\alpha _{\mathrm {T} }.}$

Kraftstoß

Für den Kraftstoß gilt:

${\displaystyle {\vec {I}}={\vec {F}}\cdot \Delta t\qquad {\text{bei }}{\vec {F}}={\text{konstant}}}$

${\displaystyle {\vec {I}}=\Delta {\vec {p}}=\int {\vec {F}}(t)\cdot \mathrm {d} t.}$