< Digitale Schaltungstechnik < Schaltalgebra
| Titelseite |
|---|
Meistens lassen sich die mit der Normalform gebildeten Gleichungen noch vereinfachen. Die Gesetze die das ermöglichen werden hier nun vorgestellt.
Leitung unterbrochen 0 Schalter offen Variable 0
Leitung durchgeschaltet Schalter geschlossen Variable 1
Allgemein
Und Verknüpfung
A und 0
Analysieren wir den Ausdruck
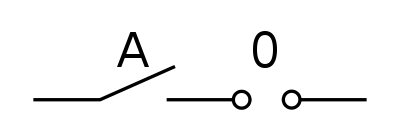
A und 1
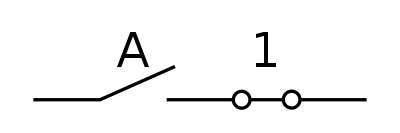
A und A
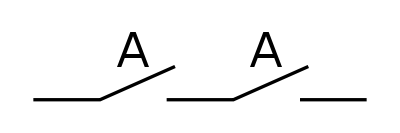
A und A
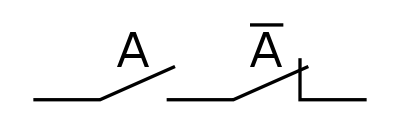
Oder Verknüpfung
A oder 0
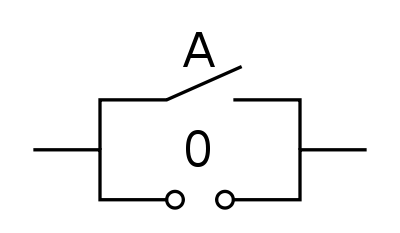
A oder 1
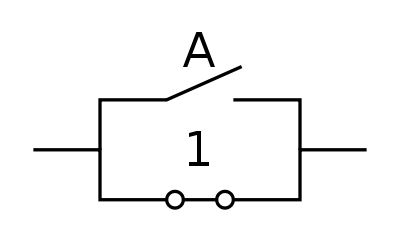
A oder A
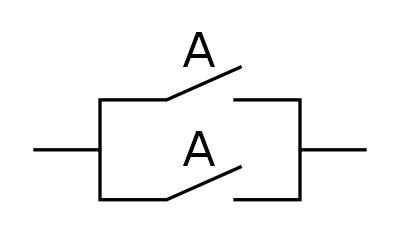
A oder A
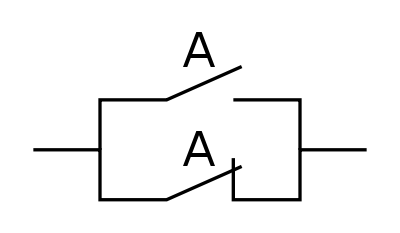
Kommutativgesetz (Vertauschungsgesetz)
Variablen mit gleicher Verknüpfung dürfen beliebig angeordnet werden.
Und
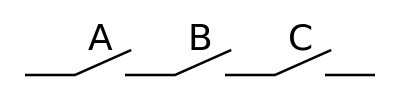
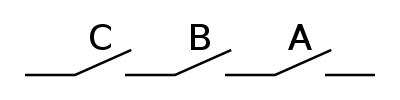
Oder
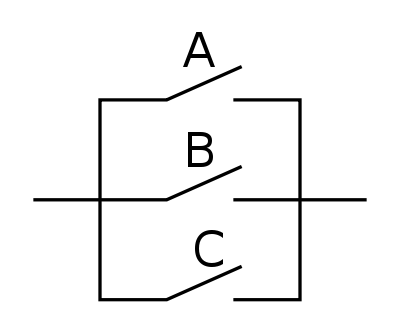

Assoziativgesetz (Verbindungsgesetz bzw. Zuordnungsgesetz)
Bei Variablen mit gleicher Verknüpfung können Klammern beliebig gesetzt werden.
Distributivgesetz (Verteilungsgesetz)
Ausklammern und Ausmultiplizieren gibt es auch in der Schaltalgebra.
.svg.png.webp)
_or_(A_and_C).svg.png.webp)
Doppelte Negationen
Doppelte Negationen heben sich auf.
Vereinfachung
Im Kapitel Wahrheitstabelle haben wir diese Gleichung ausgelesen:
Vereinfachen wir sie nun mit den neuen Regeln:
| ausklammern | |
|---|---|
| ausklammern | |
| Resultat |
Durch das Ausklammern ergeben sich mehrere Möglichkeiten, die praktisch gleich gut sind.
This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.