Audiokommentierte Folien - Wiki2Reveal

Diese Wikiversityseite ist als Foliensatz für Wiki2Reveal erstellt worden. Dies Präsentation wird in den Kursen:

• Kurs:Funktionentheorie
• Kurs:Funktionalanalysis

verwendet.

Topologischer Raum

Ein Topologischer Raum ist der grundlegende Gegenstand der Teildisziplin Topologie der Mathematik. Durch die Einführung einer topologischen Struktur auf einer Menge lassen sich

• intuitive Lagebeziehungen wie „Nähe“ und
• „Konvergenz gegen“ aus den reellen Zahlen ${\displaystyle {\mathbb {R} }}$ bzw. aus dem ${\displaystyle {\mathbb {R} }^{n}}$

auf viele und sehr allgemeine Strukturen übertragen (wie z.B. die Topologie von Funktionenräumen).

Definition: Topologie

Eine Topologie ist ein Mengensystem ${\displaystyle {\cal {T}}}$ bestehend aus Teilmengen (offene Mengen genannt) einer Grundmenge ${\displaystyle X}$, für die die folgenden Axiome erfüllt sind

• (T1) ${\displaystyle \emptyset ,X\in {\cal {T}}}$
• (T2) ${\displaystyle U\cap V\in {\cal {T}}}$ für alle ${\displaystyle U,V\in {\cal {T}}}$.
• (T3) Für eine beliebige Indexmenge ${\displaystyle I}$ und ${\displaystyle U_{i}\in {\cal {T}}}$ für alle ${\displaystyle i\in I}$ gilt: ${\displaystyle \bigcup _{i\in I}U_{i}\in {\cal {T}}}$.

Eine Menge ${\displaystyle X}$ zusammen mit einer Topologie ${\displaystyle {\cal {T}}}$ auf ${\displaystyle X}$ heißt topologischer Raum ${\displaystyle (X,{\cal {T)}}}$.

Beispiel: Topologie auf Texten

In der Regel geht man davon aus, dass Topologien auf mathematischen Objekten definiert werden (z.B. Zahlenräume, Funktionenräume, (topologische) Gruppen, Vektorräume, ...). Die Allgemeinheit der Definition macht es aber auch möglich, eine Topologie auf Texten zu definieren. Dieses Beispiel wurde ergänzt, weil rein anschaulich z.B. Texte in der deutschen Sprache

• eine ähnliche Aussage haben können und
• unterschiedliche Wörter verwenden.

Diese Ähnlichkeit der Semantik oder auch Syntax wird als Übung in "Topologie auf Texten" näher untersucht.

Bedeutung: Notation Topologie

• (T1) ${\displaystyle \emptyset ,X\in {\mathcal {T}}}$ leere Menge und die Grundmenge ${\displaystyle X}$ sind offene Mengen
• (T2) ${\displaystyle U\cap V\in {\mathcal {T}}}$ für alle ${\displaystyle U,V\in {\mathcal {T}}}$: Der Durchschnitt endlich vieler offener Mengen ist eine offene Menge.
• (T3) Die Vereinigung beliebig vieler offener Mengen ist wieder eine offene Menge.

Semantik: Metrik

Eine Metrik ${\displaystyle d}$ ordnet mit ${\displaystyle d(x,y)}$ zwei Elementen ${\displaystyle x,y\in X}$ aus einem Grundraum ${\displaystyle X}$ den Abstand ${\displaystyle d(x,y)}$ zwischen ${\displaystyle x}$ und ${\displaystyle y}$ zu.

Definition: Metrik

Sei ${\displaystyle X}$ eine beliebige Menge. Eine Abbildung ${\displaystyle d\colon X\times X\to \mathbb {R} }$ heißt Metrik auf ${\displaystyle X}$, wenn für beliebige Elemente ${\displaystyle x}$, ${\displaystyle y}$ und ${\displaystyle z}$ von ${\displaystyle X}$ die folgenden Axiome erfüllt sind:

• (M1) Trennung: ${\displaystyle d\left(x,y\right)=0\Leftrightarrow x=y}$,
• (M2) Symmetrie: ${\displaystyle d\left(x,y\right)=d(y,x)}$,
• (M3) Dreiecksungleichung: ${\displaystyle d\left(x,y\right)\leq d(x,z)+d(z,y)}$.

Veranschaulichung: Metrik Dreiecksungleichung

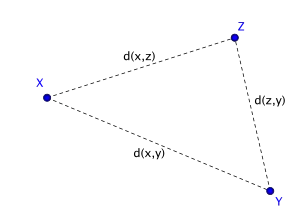
Nicht-Negativität

Aus den drei Eigenschaften der Metrik folgt die Nicht-Negativität, d.h. für alle ${\displaystyle x,y\in X}$ gilt. ${\displaystyle d(x,y)\geq 0}$. Die Nicht-Negativität folgt aus den anderen Eigenschaften mit:

${\displaystyle 0={\frac {1}{2}}d(x,x)\leq {\frac {1}{2}}(d(x,y)+d(y,x))=}$

${\displaystyle ={\frac {1}{2}}(d(x,y)+d(y,x))={\frac {1}{2}}(d(x,y)+d(x,y))=d(x,y).}$

Offene Mengen in metrischen Räumen

• In einem metrische Raum ${\displaystyle (X,d)}$ definiert man eine Menge ${\displaystyle U\subset X}$ als offen (d.h. ${\displaystyle U\in {\mathcal {T}}_{d}}$), wenn es zu jedem ${\displaystyle u\in U}$ ein ${\displaystyle \epsilon >0}$ gibt, dass die ${\displaystyle \epsilon }$-Kugel ${\displaystyle B_{\epsilon }^{d}(u):=\{\ x\in X|\ d(x,u)<\epsilon \}}$ ganz in ${\displaystyle U}$ liegt (d.h. ${\displaystyle B_{\epsilon }^{d}(u)\subset U}$)
• Zeigen Sie, dass mit diesem definierten ${\displaystyle {\mathcal {T}}_{d}}$ das Paar ${\displaystyle (X,{\mathcal {T}}_{d})}$ ein topologischer Raum ist (d.h. (T1), (T2), (T3) erfüllt).

Norm auf Vektorräumen

Eine Norm ist eine Abbildung ${\displaystyle \|\cdot \|}$ von einem Vektorraum ${\displaystyle V}$ über dem Körper ${\displaystyle \mathbb {K} }$ der reellen oder der komplexen Zahlen in die Menge der nichtnegativen reellen Zahlen ${\displaystyle {\mathbb {R} }_{0}^{+}}$. Dabei ordnet die Norm jedem Vektor ${\displaystyle x\in V}$ seine Länge ${\displaystyle \|x\|}$ zu.

Definition: Norm

Sei ${\displaystyle V}$ ein ${\displaystyle \mathbb {K} }$-Vektorraum und ${\displaystyle \|\cdot \|\colon V\to {\mathbb {R} }_{0}^{+},\;x\mapsto \|x\|,}$ eine Abbildung Erfüllt ${\displaystyle \|\cdot \|}$ die folgenden Axiome Axiome N1,N2, N3, so heißt ${\displaystyle \|\cdot \|}$ Norm auf ${\displaystyle V}$.

• (N1) Definitheit: ${\displaystyle \|x\|=0\;\Rightarrow \;x=\mathbb {0} }$ für alle ${\displaystyle x\in V}$,
• (N2) absolute Homogenität: ${\displaystyle \|\lambda \cdot x\|=|\lambda |\cdot \|x\|}$ für alle ${\displaystyle x\in V}$ und ${\displaystyle \lambda \in \mathbb {K} }$
• (N3) Dreiecksungleichung: ${\displaystyle \|x+y\|\leq \|x\|+\|y\|}$ für alle ${\displaystyle x,y\in V}$.

Bemerkung: N1 - Äquivalenz

Das Eigenschaft (N1) ist eigentlich eine Äquivalenz und es gilt in jedem normierten Raum (${\displaystyle \mathbf {0} \in V}$ ist der Nullvektor in ${\displaystyle V}$ und ${\displaystyle 0\in \mathbb {K} }$ ist die Null im Körper ${\displaystyle \mathbb {K} }$, wenn ${\displaystyle V}$ ein ${\displaystyle \mathbb {K} }$-Vektorraum ist).

• (N1)' Definitheit: ${\displaystyle \|x\|=0\;\Leftrightarrow \;x=\mathbf {0} }$ für alle ${\displaystyle x\in V}$,
• Da man für Definitionen ein Minimalitätsprinzip für die definierenden Eigenschaft verwendet, würde man keine stärkere Formulierung (N1)' in der Definition für (N1) verwenden, da die Äquivalenz aus den definierenden Eigenschaften der Norm den Eigenschaften des Vektorraumes bereits für jeden normierten Raum folgen.

${\displaystyle x\equiv \mathbf {0} \Rightarrow \|x\|=\|0\cdot \mathbf {0} \|=|0|\cdot \|\mathbf {0} \|=0}$

Normierter Raum / Metrischer Raum

Ein normierter Raum ${\displaystyle (V,\|\cdot \|)}$ ist zugleich auch ein metrischer Raum.

• Ein Norm ${\displaystyle \|\cdot \|}$ ordnet einem Vektor ${\displaystyle v\in V}$ seine Vektorlänge ${\displaystyle \|v\|}$ zu.
• Mit der Norm ${\displaystyle \|\cdot \|}$ kann man über ${\displaystyle d(x,y):=\|x-y\|}$ eine Metrik definieren.
• Zeigen Sie, dass die so definierte Abbildung ${\displaystyle d:V\times V\rightarrow \mathbb {R} }$ die Eigenschaften einer Metrik erfüllt.

Notation: Norm

• In dem Axiom (N2) ${\displaystyle \|\lambda \cdot x\|=|\lambda |\cdot \|x\|}$ bezeichnet ${\displaystyle |\cdot |}$ den Betrag des Skalars. "${\displaystyle \cdot }$"-Zeichen: Äußere Verknüpfung im Vektorraum bzw. Multiplikation ${\displaystyle (\mathbb {R} ,\cdot )}$.
• ${\displaystyle \|x\|}$ gibt die Länge des Vektors ${\displaystyle x\in V}$ an.
• In (N3) ${\displaystyle \|x+y\|\leq \|x\|+\|y\|}$ für alle ${\displaystyle x,y\in V}$. "${\displaystyle +}$"-Zeichen bezeichnet zwei unterschiedliche Verknüpfungen (d.h. Addition in ${\displaystyle (V,+)}$ bzw. ${\displaystyle (\mathbb {R} ,+)}$

Veranschaulichung: Norm Dreiecksungleichung

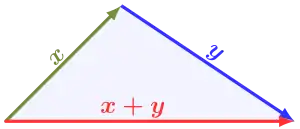
Def: Konvergenz im normierten Raum

Sei ${\displaystyle (V,\|\cdot \|)}$ ein normierter Raum und ${\displaystyle (v_{n})_{n\in \mathbb {N} }\in V^{\mathbb {N} }}$ eine Folge in ${\displaystyle V}$ und ${\displaystyle v_{o}\in V}$:

${\displaystyle \lim _{n\to \infty }^{\|\cdot \|}v_{n}=v_{o}\$ :\Longleftrightarrow \ \forall _{\epsilon >0}\exists _{n_{\epsilon }\in \mathbb {N} }\forall _{n\geq n_{\epsilon }}\ :\ \|v_{n}-v_{o}\|<\epsilon }

Def: Konvergenz im metrischen Raum

Sei ${\displaystyle (X,d)}$ ein metrischer Raum und ${\displaystyle (x_{n})_{n\in \mathbb {N} }\in X^{\mathbb {N} }}$ eine Folge in ${\displaystyle X}$ und ${\displaystyle x_{o}\in X}$:

${\displaystyle \lim _{n\to \infty }^{d}x_{n}=x_{o}\$ :\Longleftrightarrow \ \forall _{\epsilon >0}\exists _{n_{\epsilon }\in \mathbb {N} }\forall _{n\geq n_{\epsilon }}\ :\ d(x_{n},x_{o})<\epsilon }

Äquivalenz: Normen

Seien zwei Normen ${\displaystyle \|\cdot \|_{1}}$ und ${\displaystyle \|\cdot \|_{2}}$ auf dem ${\displaystyle \mathbb {K} }$-Vektorraum ${\displaystyle V}$ gegeben. Die beiden Normen sind äquivalent, wenn gilt:

${\displaystyle \exists _{C_{1},C_{2}>0}\forall _{x\in V}\$ :\ C_{1}\|x\|_{1}\leq \|x\|_{2}\leq C_{2}\|x\|_{1}}

Zeigen Sie, dass eine Folge genau dann in ${\displaystyle \|\cdot \|_{1}}$ konvergiert, wenn es auch bzgl. ${\displaystyle \|\cdot \|_{2}}$ konvergiert.

Betrag in komplexen Zahlen

Sei ${\displaystyle z=z_{1}+i\cdot z_{2}\in \mathbb {C} }$ eine komplexe Zahl mit ${\displaystyle z_{1},z_{2}\in \mathbb {R} }$. Zeigen Sie, dass ${\displaystyle |z|:={\sqrt {z\cdot {\overline {z}}}}}$ eine Norm auf dem ${\displaystyle \mathbb {R} }$-Vektorraum ${\displaystyle \mathbb {C} }$ ist!

Historische Anmerkung: Norm

Diese axiomatische Definition der Norm wurde von Stefan Banach 1922 in seiner Dissertation aufgestellt Das heute übliche Normsymbol wurde erstmals von Erhard Schmidt 1908 als Abstand ${\displaystyle \|x-y\|}$ zwischen Vektoren ${\displaystyle x}$ und ${\displaystyle y}$ verwendet.

Aufgaben

Zeigen Sie, dass die folgende Abbildung ${\displaystyle d}$ auf ${\displaystyle V:={\mathcal {C}}([a,b],\mathbb {R} )}$ mit ${\displaystyle a,b\in \mathbb {R} }$ als Menge der stetigen Abbildungen von dem Intervall ${\displaystyle [a,b]}$ nach ${\displaystyle \mathbb {R} }$ eine Metrik ist.

${\displaystyle d:V\times V\to \mathbb {R} }$ mit ${\displaystyle (f,g)\mapsto d(f,g):=\int _{a}^{b}|f(x)-g(x)|\,dx\ .}$

Weisen Sie also die 3 Eigenschaften einer Metrik ${\displaystyle d}$ nach. Berechnen Sie dann den Abstand zwischen den beiden Funktionen ${\displaystyle f(x):=x^{2}}$ und ${\displaystyle g(x):=x^{3}-2x+2}$ mit ${\displaystyle a=-1}$ und mit ${\displaystyle b=3}$!

Siehe auch

• Epidemiologische Distanzen
• Normenäquivalenzsatz
• COVID-19/Mathematische Modellbildung - für epidemiologische Distanzen im Unterschied zu euklidischen Distanzen in einem Vektorraum.

Seiteninformation

Diese Lernresource wurde als Wiki2Reveal Foliensatz erstellt.