< Geogebra

Aufgabe für Lernende

  • (Theoretischer Hintergrund) Analysieren Sie den theoretischen Hintergrund[1] für das perspektivische Zeichnen, bei dem als nicht-digitale Umgebung ein Spiegel als Projektionsfläche verwendet wird, auf den z.B. mit einem Folienstift das perspektivische Bild eingezeichnet wird.
  • (Geogebra-Konstruktion) Ausgehend von dieser Situation des perspektivischen Zeichnens von Objekten auf einem Spiegel werden nun die Konstruktionen in Geogebra behandelt:
    • Z-Konstruktion für die Projektion von Halbgeraden,
    • X-Konstruktion für die Projektion von Punkten als Schnittpunkt von zwei Halbgeraden. Dabei wird der Bildpunkt über zwei Z-Konstruktionen generiert.
    • I-Konstruktion für die Projektion einer senkrecht stehenden Strecke, die über zwei X-Konstruktionen erzeugt wird.
  • (Projektion von Kreisen) Überlegen Sie, wie Sie mit einer Ortslinie und einer X-Konstruktion das projektive Bild eines Kreise erstellen können.
  • (Projektion von einer Sinus-Kurve) Überlegen Sie, wie Sie mit einer Ortslinie und einer X-Konstruktion das projektive Bild einer Sinuskurve in der Standebene erstellen können.

Einführung

Bei dieser Lernressource geht es um die perpective Zeichnung von 3D-Objekten auf einem Spiegel und um die geometrischen Prinzipien der Konstruktion. Zusammen mit dieser Lernressource ein GitHub-Repository mit Geogebra-Dateien[2] wurde erstellt, die mit dynamischer Geometrie-Software geöffnet werden kann Geogebra. Die Konstruktion basiert auf einem deutschen Artikel in der Zeitschrift Mathematica Didactica 26 (2003) Bd.1 43, Experimenteller Umgang mit Spiegelung und Perspektive unter Verwendung von Dynamischer Geometriesoftware, Engelbert Niehaus[3]

3D Konstruktion von Projektionen in Geogebra

Das Repository enthält Geogebra-Dateien zum Erlernen von 3D-Projektionen auf einem Spiegel Z-, X- und I-Konstruktion von 3D-Punkten und Linien. Dieses Repository verfügt über zusätzliches Lernmaterial für die Open Source Software Geogebra und die Datei ist in einem GitHub Repository gebündelt, das ursprünglich für die englische Lernresource Perspective Drawing on Mirror erstellt wurde.

3D-Konstruktion von Projektionen in Geogebra

Das folgende Bild zeigt die Grundsituation einer 3D-Projektion auf einem Spiegel. Das perspektivische Bild der Box ist auf den Spiegel gemalt.

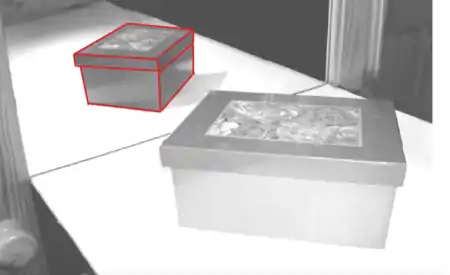
Grundlegende Situation vor dem Spiegel

Verwenden Sie ein Papier als Vermittler zwischen der 3D-Welt und der 2D-Konstruktion.

Sie können ein Papier als Vermittler zwischen der 3D-Welt und der 2D-Projektion auf dem Papier verwenden und durch das Aufklappen die wesentlichen Konstruktionselemente (wie Spurgerade, Horizont und Augenpunkt) auf dem Papier und der 3D-Situation vor dem Spiegel sichtbar machen.

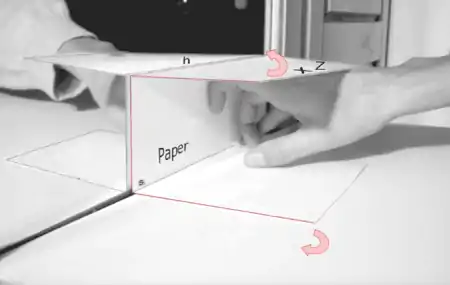
Konstruktion

Die perspektivische Zeichnung erzeugt ein Bild eines Objekts vor einem Spiegel. Das Auge beobachtet das projektive Bild von einem Punkt Z aus. Angenommen, der Betrachter malt das perspektivische Bild einer vertikalen Stange auf die Oberfläche des Spiegels.


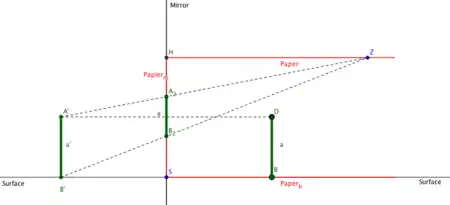
Z-Konstruktion für Halbgerade in der Ebene

Wir entfalten den Papiervermittler zwischen 2D und 3D Konstruktion und übertragen die Faltung auf zwei parallele Linien in Geogebra. Eine Z-Konstruktion erzeugt perspektivisches Bild einer Halbgerade.

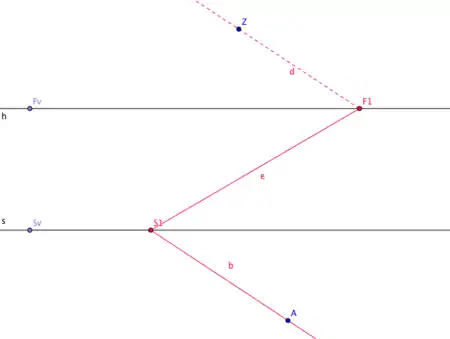
X-Konstruktion für Point on a Surface

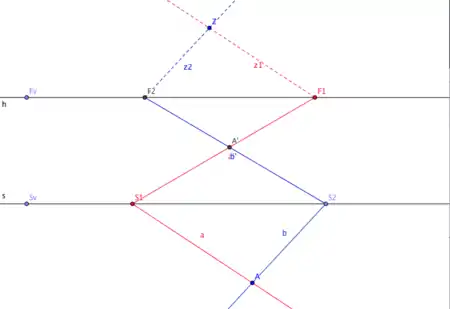
Die X-Konstruktion erzeugt ein perspektivisches Bild eines Punktes, der als Schnittpunkt von zwei Halbgerade eindeutig bestimmt ist. Der Bildpunkt ist damit durch zwei Z-Konstruktionen.

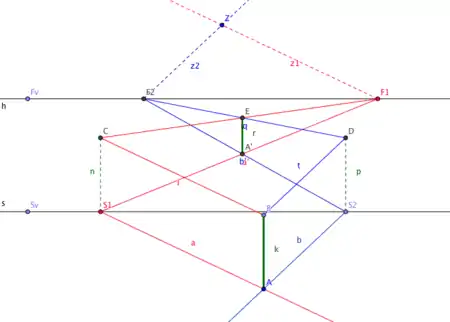
I-Construction for a Vertical Line

Eine I-Konstruktion erzeugt ein perspektivisches Bild einer vertikalen Linie oder Stabes, der dann über zwei X-Konstruktionen als Bild der vertikalen Linie erzeugt wird.

Siehe auch

Externe Quellen

Quellennachweis/Literatur


  1. ↑ Engelbert Niehaus (2003), Experimenteller Umgang mit Spiegelung und Perspektive unter Verwendung von Dynamischer Geometriesoftware, Mathematica Didactica 26, Bd. 1 43, URL: http://mathematica-didactica.com/altejahrgaenge/md_2003/md_2003_1_Niehaus_Spiegelung.pdf (access 2020/11/24)
  2. ↑ 3D-Konstruktion mit Geogebra (2017-2019) Engelbert Niehaus, URL: Https://github.com/niebert/3D_Construction_Geogebra (zugegriffen am 2019.06.12)
  3. ↑ Niehaus, Engelbert (2003), Experimenteller Umgang mit Spiegelung und Perspektive unter Verwendung von Dynamischer Geometriesoftware, Mathematica Didactica 26 (2003) Bd.1 43,
This article is issued from Wikiversity. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.