< Digitale Schaltungstechnik < Flipflop
| Titelseite |
|---|
|
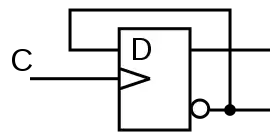
Nicht bedingtes Toggeln

Wahrheitstabelle
| Wahrheitstabelle | |
|---|---|
| C | Q |
| 0 | 0 |
| / | 1 |
| \ | 1 |
| / | 0 |
| \ | 0 |
Oder allgemeiner:
| Wahrheitstabelle | ||
|---|---|---|
| C | Q | |
| 0 | ||
| / | ||
| 1 | ||
| \ | ||
Beschränken wir uns auf das Wesentliche, sieht die Tabelle so aus:
| Wahrheitstabelle | ||
|---|---|---|
| T | Q | |
| / | ||
Bei jeder positiven Taktflanke ändert sich das Ausgangssignal
Impulsdiagramm
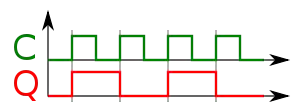
Wie hier im Impulsdiagramm zu erkennen ist, ist die Ausgangsfrequenz halb so groß wie die Eingangsfrequenz.
Spezifische Gleichung
Bedingtes Toggeln

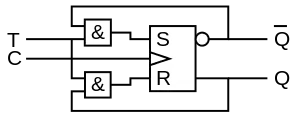
Wenn das Toggeln gesteuert werden soll, lässt sich das über einen weiteren Eingang realisieren.
Wahrheitstabelle
| Wahrheitstabelle | ||
|---|---|---|
| T | C | Q |
| 0 | / | |
| 1 | / | |
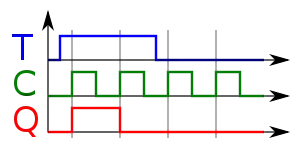
Dass das Flipflop nicht bei jeder Flanke toggelt, ist vor allem bei synchronen Schaltungen (wie wir sie später kennenlernen werden) relevant: Dort werden bewusst alle Takteingänge zusammen geschaltet.
Impulsdiagramm
Ersatzschaltbild
Spezifische Gleichung
Anwendungen
Hauptanwendung:
- Asynchrone Zähler
- Frequenzteiler
This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.