Theoretische Physik 1 - Mechanik
Hinweis: Gesucht werden Autoren und Korrektoren
- Wolf (Student / wenig Zeit)
N.N.
- Nolting - Theoretische Physik 1
Sporadisch
Mathematische Grundlagen
Einstein'sche Summenkonvention
Die Einstein'sche Summenkonvention wurde 1916 von Einstein als Mathematische Grundlage zur Allgemeinen Relativitätstheorie vorgeschlagen und wird mittlerweile hauptsächlich in der theoretischen Physik verwendet. Sie besteht darin, das Summenzeichen wegzulassen und stattdessen über in Produkten doppelt auftretende Indizes zu summieren. Dadurch reduziert sich der Schreibaufwand. Man sollte nur stets im Hinterkopf behalten, dass es sich trotzdem um Summen handelt.
Beispiele:
Weiterführendes:
Tensoren
- Ein Tensor n.Stufe hat Elemente. Ein Tensor 2. Stufe also
Levi-Civita-Symbol
Definition
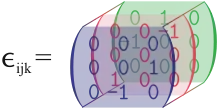
Aber was heißt das? Das Levi-Civita-Symbol ist ein invarianter, total antisymmetrischer (Pseudo-)Tensor n-ter Stufe.
Im gilt:
Daraus folgt:
Die Herleitung der Determinantenschreibweise ist als Übungsaufgabe aufgelistet, die Lösung steht dabei.
Beispiel im :
Mit als normale kartesische Einheitsvektoren:
Gerade Permutation:
Ungerade Permutation:
Zwei gleiche Indizes:
Kronecker-Delta
Das Kronecker-Delta ist ein Tensor zweiter Stufe mit zwei Indizes, i und j. Es wird hauptsächlich in Summenformeln bei Vektor- und Matrizenrechnung verwendet.
Definition
Daraus folgt im dreidimensionalem euklidischem Raum mit den Einheitsvektoren :
Beispiel
für folgt
für mit z.B. folgt:
Übungsaufgaben
Levi-Civita-und Kronecker-Delta Hinweis: Da die Übungsaufgaben aufeinander aufbauen, bietet es sich an sie in der Reihenfolge zu bearbeiten.
1.) Zeige: Lösung
2.) Zeige: Lösung
3.) Zeige: Lösung
4.) Zeige: Lösung
5.) Zeige: Lösung
6.) Zeige: Lösung (Lösung fehlt noch!)
7.) Zeige: (Lösung fehlt noch!)
Differentialoperator
* Ein Differentialoperator ist kein Vektor im eigentlichen Sinne! * Man kann Differentialoperatoren nicht kürzen oder mit ihnen erweitern! * Existiert nur an Stellen, wo die Funktion nach allen Koordinaten stetig differenzierbar ist * Satz von Schwarz für zweifach stetig differenzierbare Funktionen
Nabla
Der Nabla-Operator bildet die partiellen Ableitungen einer Funktion nach den verschiedenen Koordinaten.
Gradient
Der Gradient , auch , ist als der Vektor, der durch das partielle Ableiten eines Skalarfeldes entsteht, definiert. Er existiert nur an den Stellen, wo das Skalarfeld nach allen Koordinaten partiell stetig differenzierbar ist.
Für ein Skalarfeld im n-dimensionalem euklidischem Raum gilt:
Divergenz
Im n-dimensionalem euklidischen Raum gilt:
Rotor (oft auch Rotation)
Im n-dimensionalem euklidischen Raum gilt:
Für folgt:
Übungsaufgaben
Differentialoperatoren grad, div, rot Hinweis: Alle Skalarfelder, Vektorfelder sind zweifach stetig differenzierbar.
Koordinatentransformation
Verschiebung (Translation)
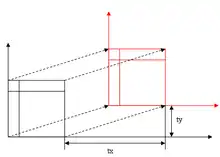
.
.
.
.
.
.
.
.
.
Drehung (Rotation)
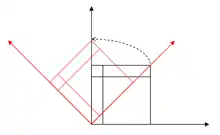
.
.
.
.
.
.
.
.
.
.
.
Raum, Zeit und Bewegung
Newton'sche Dynamik
Bewegung eines Massenpunktes
Literatur
- Nolting - Grundkurs: Theoretische Physik (Klassische Mechanik) - ISBN 3-922410-18-9
- Rebhan - Theoretische Physik: Mechanik - ISBN 3-8274-1716-3
- Fließbach, Walliser - Arbeitsbuch zur Theoretischen Physik - ISBN 3-8274-1521-7