SIR Modell über Funktionen

Im Folgenden soll die Entwicklung der Infektionszahlen in Mainz in Form einer Glockenkurve dargestellt werden. Wir wenden das SIR Modell über Funktionen an, um den Verlauf der Pandemie dementsprechend zu modellieren.

Parameter festlegen

An dieser Stelle werden die Parameter für die Infektionsrate beta, die Wechselrate gamma und die Anzahl der Tage N_t, für die Modellierung festgelegt.

beta = 0.29
gamma = 0.1
N_t = 250

Vektoren für S, I und R

Um die Entwicklung in den für die Werte, für die festgelegten Tage zu sehen, werden drei Spaltenvektoren mit gleicher Länge für die drei Gruppen S, I und R erstellt. Diese Vektoren haben nur Nullen als Werte in der Spalte stehen.

S = zeros(N_t+1, 1);

Analog werden die zwei Vektoren für I und R erstellt.

Anfangszustand für das betrachtete Beispiel

Wir benötigen Anfangswerte. Für unser Beispiel Mainz sind es diese:

 S(1) = 1;         % relativer Anteil der Einwohner in Mainz (6111.25 Einwohner)
 I(1) = 0.000025;   % relativer Anteil eines Infizierten in Mainz
 R(1) = 0;

Schleife für Epidemiologischen Prozess

Erklärung der Funktionen und der jeweilige Wechsel in die andere Gruppe:

• Die erste Funktion betrachtet die Anzahl der Empfänglichen S am Tag n+1. Dafür wird von der Anzahl der Emfänglichen am Tag zuvor (also am Tag n), die Anzahl von den Anzahl neu Infizierten (beta*S*I) subtrahiert.

• Die zweite Funktion berachtet die Infizierten im neuen Zeitschritt, dafür werden zu den alten Infizierten I(n) die Anzahl der neu Infizierten, die in der ersten Funktion abgezogenen wurden, hinzugefügt und anschließend wird der Anteil der Genesenen abgezogen (berechnet durch das Produkt gamma*I).

• Die dritte Funktion betrachtet die Genesenen, zu den bereits Gensenen (R(n)) wird der Anteil der Gensenen, die in der zweiten Funktion abgezogen wurden, hinzugefügt.

Mit Hilfe der Schleife, wird für jeden nächsten Schritt die Werte für die Funktionen S, I und R berechnet.

   for  n = 1:N_t
      S(n+1) = S(n) - beta * S(n) * I(n);
      I(n+1) = I(n) + beta * S(n) * I(n) - gamma * I(n);
      R(n+1) = R(n) + gamma * I(n);
   endfor   

Graphische Darstellung

SIR Modell am Beispiel Mainz

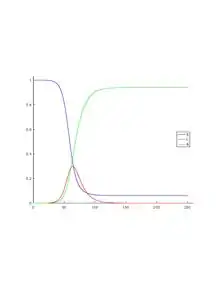
Siehe Bild: SIR Modell am Beispiel Mainz

.

Schachbrettmuster

Ziel der folgenden Aufgabe ist es, die Entwicklung der räumlichen Verbreitung des Virus zu modellieren.

Dazu legen wir in den Schritten 1-2 eine Ausgangssituation der Virusverbreitung fest und in den Schritten 3-7 fügen wir dem Modell die zeitliche Veränderung der Verbreitung hinzu.

Schritt 1

Zunächst erzeugen wir ein Schachbrettmuster mit einer Dimension von 50x50.

Schachbrettmuster

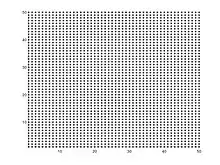
N_x=50;
N_y=50;
x=[1:N_x];
y=[1:N_y];
[x,y]=meshgrid(x,y);

figure (1)
hold on;
plot(x,y,'*k')
axis([1 50 1 50]);
hold off;

Jeder Knoten-/Gitterpunkt stellt einen bestimmten Ort eines betrachteten Raums dar. Wenn wir uns z.B. eine Großstadt anschauen, kann sich an einem Knotenpunkt der Hauptbahnhof befinden, ein anderer Knotenpunkt kann ein Einkaufszentrum abbilden usw.. Mit diesem Schachbrett werden wir eine räumliche Darstellung der Virusverbreitung erstellen.

Schritt 2

Wir benötigen nun Anfangswerte für S, I und R, die die folgende Ausgangssituation abbilden sollen: In einer bisher vom Virus unbetroffenen Stadt beginnt die Infizierung an einem Ort, z.B. durch einen am Bahnhof angekommenen Touristen. Die Matrix I muss demnach fast nur aus Nullen bestehen. Nur der Wert, der den Ort des Infektionsbeginns darstellt, ist gleich 1. Da es noch keinen Genesenen gibt, ist die R Matrix anfangs eine Nullmatrix und S besteht aus zufälligen Anfangswerten.

S_0=rand(50)*1000000
I_0=zeros(50)
I_0 (33,33)=1;
R_0=zeros(50)

Schritt 3

Um berechnen zu können, wie sich die Infektionen in den folgenden 250 Tagen entwickeln werden, müssen wir folgende Parameter festlegen:

beta = 0.29
gamma = 0.1
N_t = 250

Dabei steht beta für die Infektionsrate, gamma für die Wechselrate und N_t für die Anzahl der Tage.

Schritt 4

Die Anfangsbedingungen werden als Matrizen dargestellt

S_alt=S_0;
I_alt=I_0;
R_alt=R_0;

Schritt 5

Wir definieren Funktionen, die entsprechend der Parameter zum Infektionsgeschehen (siehe Schritt 3) neue Werte für die Matritzen S, I und R berechnen.

function   
     S_neu=EpiS(pS,pI,pR,pbeta,pgamma);
     S_neu=pS-(pS.*pI)*pbeta;
endfunction 

Analog werden mit den jeweiligen Formeln, auch die Funktionen für I und R als Matrizen dargestellt.

Schritt 6

Auch für die Zeititeration müssen wir eine Funktion aufstellen. Durch diese Funktion sind die Werte eines beliebigen Tages abrufbar. So wurden z.B. im Folgenden in der letzten Zeile der Implementierung die Werte des dritten Tages abgerufen.

function S_neu=ZeititerationS(pS,pI,pR,pbeta,pgamma,pN_t);
     S_alt=pS;
     I_alt=pI;
     R_alt=pR;
        for n=1:pN_t
            S_neu=EpiS(S_alt,I_alt,R_alt,pbeta,pgamma);
            S_neu(find(Sneu<0))=0; 
            I_neu=EpiI(S_alt,I_alt,R_alt,pbeta,pgamma);
            R_neu=EpiR(S_alt,I_alt,R_alt,pbeta,pgamma);
            S_alt=S_neu;
            I_alt=I_neu;
            R_alt=R_neu;
        endfor 
endfunction 
S_neu,I_neu,R_neu=ZeititerationS(S_0,I_0,R_0,beta,gamma,3),

Schritt 7 / Optimierung

Um sicher zu stellen, dass keine negativen Werte für S entstehen, fügen wir der Zeititerationsfunktion folgende Bedingung hinzu:

    S_neu(find(S_neu<0))=0;

Transportmatrix

Zufällige Transportmatrix

Da für die Orte eine 50x50 Matrix gewählt wurde, muss für die Transportmatrix eine 2500x2500 Matrix generiert werden. Zunächst wird diese zufällig gewählt. Dabei muss die Summe der einzelnen Spalten 1 ergeben (also 100%), da sich in einem Ort die Gesamtpersonenzahl nicht ändert auch wenn es Infizierte und Geheilte (hier werden die Toten mit dazu gezählt) gibt.

for j=1:2500
   x=rand(100,1);
   x=x/sum(x); 
   T(1:2500,j)=x;
endfor

Anwendung auf Anfangsmatrix der Succesible

Um die 2500x2500-Transportmatrix auf die 50x50-S₀-Matrix anwenden zu können, muss die S₀-Matrix in einen langen 2500x1 Vektor umgeformt werden (Denn sonst kann man sie nicht mit einer 50x50 Matrix multiplizieren). Nach der Matrizenmultiplikation kann der entstandene Vektor wieder in eine 50x50-Matrix umgeformt werden.

MeshT

A=/reshape(S_0,2500,1);
Neu=T*A;
B=reshape(Neu,50,50)

Der Zufall ist hier ungeschickt gewählt, da die Menschen willkürlich den Ort wechseln, was in Wirklichkeit nicht der Fall ist. Siehe Bild MeshT.

Verbesserte Transportmatrix

Nun berücksichtigen wir, dass die meisten Menschen den Ort nicht wechseln. Dies entspricht der Diagonale auf der Transportmatrix (Siehe Bild MeshTneu im Vergleich zu MeshT). Dazu soll zunächst eine Matrix mit passenderen Werten erstellt werden, die im nächsten Schritt normiert wird, sodass die einzelnen Spalten der Matrix wieder 1 ergeben.

MeshTneu

Für die Diagonale werden nun Werte zwischen 1250 und 2250 festgelegt.

x=rand(1,2500)*1000+1250;
v(1:2500)=x;          
D=diag(v,0);

Dazu wird eine zweite Matrix mit Werten zwischen 0 und 50 festgelegt. Alternativ hätte man die Werte hier auch kleiner wählen können.

B=rand(2500,2500)*50;

Die beiden Matrizen werden im nächsten Schritt addiert und anschließend normiert.

C=D+B;
for n=1:2500
   j=sum(C(:,n)); 
   X=(C(:,n)/j);
   T_{neu}(1:2500,n)=X;
endfor
T_{neu}

Transportmatrix mit Berücksichtigung der Distanz

Für die Ortswechsel soll nun die Distanz der einzelnen Orte berücksichtigt werden. Je näher Orte aneinander liegen, desto eher findet ein Austausch statt. Eine Möglichkeit die Distanz zu berücksichtigen ist, diese reziprok in die Transportmatrix einzubauen. Dadurch folgt, je näher die Orte, desto größer der Wert in der Matrix. Damit jedoch nicht durch Null geteilt wird, wenn der Abstand eines Ortes zu sich selbst bestimmt wird, wird ${\displaystyle {\frac {1}{1+dist}}}$ eingesetzt.

 Allgemein wird die Distanz für zwei Punkte (x1,x2) und (y1,y2) folgendermaßen berechnet:

distmat = sqrt((x1-y1).^2+ (x2-y2).^2)

Zunächst wird die Distanz in einer Funktion definiert.

[xx,yy]=meshgrid(1:50); 
YYY=[]; 
hh=[];   
for i = 1:50; 
for j = 1:50;
distmat = sqrt((xx-j).^2+ (yy-i).^2); 
hh=[hh;reshape(distmat',1,2500)];
YY=1./(1.+distmat);  
YYY=[YYY; reshape(YY',1,2500)]; 
endfor
endfor

MeshYYY

ContourYYY

ImshowYYY

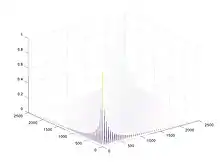
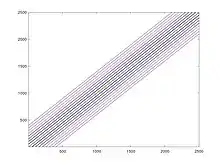
In einer Schleife wurde ein Vektor YY gebildet, der die Distanz zwischen allen Punkten in der Form ${\displaystyle {\frac {1}{1+dist}}}$ enthält. Anschließend wurde der Vektor in eine 100x100-Matrix überführt.

Die Distanzmatrix kann man auf folgende Weisen darstellen: s.Bilder MeshYYY, ContourYYY, ImshowYYY