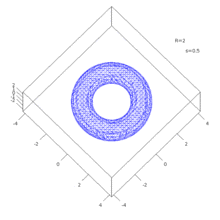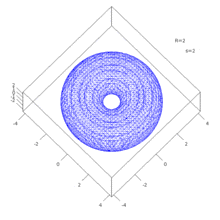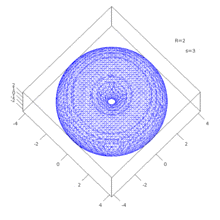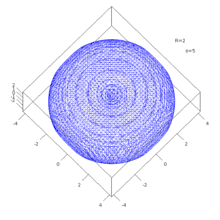
Die regulären Punkte erhält man durch das totale Differential: Die singulären Punkte bilden einen Kreis mit dem Radius R in der x-y-Ebene mit dem Nullpunkt in der Mitte (der der einzie singuläre Punkt ist, der nicht auf dem Kreis liegt), alle anderen Punkte sind regulär.
Die nebenstehende Animation zeigt beispielhaft für R=2 die Fasern für verschiedene s. Deutlich zu sehen ist, wie sich bei s=4=√(R) das Loch im Torus schließt.

Animation zur Veranschaulichung von Aufgabe 79.27.

Von Lukas Freudenberg.