Kurs:Funktionentheorie/Lemma von Goursat (Details)

Das Lemma von Goursat, manchmal auch als Satz von Goursat bezeichnet, ist ein Satz aus der Funktionentheorie.

Das Lemma von Goursat ist eine Vorstufe des Cauchyschen Integralsatzes und wird auch oft für dessen Beweis genutzt. Es spielt im Aufbau der Funktionentheorie eine wichtige Rolle. Bemerkenswert ist, dass das Lemma lediglich die komplexe Differenzierbarkeit voraussetzt, nicht aber die stetige Differenzierbarkeit. Das Lemma wurde von Édouard Goursat (1858-1936) in der Rechteckform bewiesen und 1884 veröffentlicht. Die heute übliche Dreiecksform stammt von Alfred Pringsheim.

Satz von Goursat

Gegeben sind die folgenden Voraussetzungen:

(P1) Sei ${U}\subseteq \mathbb {C}$ eine offene Teilmenge,
(P2) Seien ${z}_{1},{z}_{2},{z}_{3}\in \mathbb {C}$ drei nicht kollineare Punkte, die das Dreieck

\Delta {\left({z}_{1},{z}_{2},{z}_{3}\right)}:=\left\{\sum _{k=1}^{3}\lambda _{k}\cdot {z}_{k}{\mid }{\left({\sum _{{k}{1}}^{3}}\lambda _{k}={1}\right)}\wedge \forall {k}\in {\left\lbrace {1},{2},{3}\right\rbrace }\lambda _{k}\in [{0},{1}]\right\}\subset {U}

definieren,

(P3) Sei ${f}:{U}\to \mathbb {C}$ eine holomorphe Funktion,
(P4) Sei ${\left\langle {z}_{1},{z}_{2},{z}_{3}\right\rangle }:{\left[{0},{3}\right]}\to \mathbb {C}$ der geschlossene Weg über den Dreiecksrand von $\Delta {\left({z}_{1},{z}_{2},{z}_{3}\right)}$ mit Startpunkt ${z}_{1}$ .

dann folgt die folgenden Behauptungen gelten:

(C1) $\int _{\left\langle {z}_{1},{z}_{2},{z}_{3}\right\rangle }{f{\left({z}\right)}}{d}{z}={0}$

Beweis

Integrationsweg auf dem Dreiecksrand

Aufteilung der äußeren Wegen und Einfügen von zusätzlichen Wegen zwischen den Seitenmitten, die sich durch die umgekehrte Richtung des Integrationsweges im Wegintegral als Summe 0 ergeben und somit das Gesamtintegral nicht verändern.

Induktive Definition der Wege. Die Teildreieck sind ähnlich zum Ausgangsdreieck. Durch die Verwendung der Seitenmitten halbiert sich jeweils der Umfang von einem Dreieck

\Delta ^{(n)}

zu

\Delta ^{(n+1)}

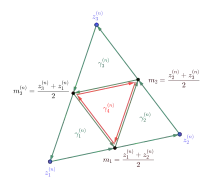
(S1) Wir definieren wird eine Folge von Dreieickswegen rekursiv $\gamma ^{(n)}:={\left\langle z_{1}^{(n)},z_{2}^{(n)},z_{3}^{(n)}\right\rangle }$

Beweisteil 1: Definition der Dreieckswege

(S2) (DEF) Für ${n}={0}$ sei der geschlossene Dreiecksweg $\gamma ^{(0)}:[0,3]\to \mathbb {C}$ mit:

\gamma ^{(0)}(t):=\left\langle z_{1},z_{2},z_{3}\right\rangle (t):={\begin{cases}(1-t)\cdot z_{1}+t\cdot z_{2}&{\text{für}}t\in [0,1]\\(2-t)\cdot z_{2}+(t-1)\cdot z_{3}&{\text{für}}t\in (1,2]\\(3-t)\cdot z_{3}+(t-2)\cdot z_{1}&{\text{für}}t\in (2,3]\\\end{cases}}

Ferner sei und $\gamma ^{(n)}$ bereits definiert. Wir definieren nun $\gamma ^{(n+1)}$ induktiv.

Begründung: (P4,UT)

(S3) (DEF) Definition: Dreiecksweg ${\gamma _{1}^{(n)}}:={\left\langle {\frac {z_{1}^{(n)}+z_{2}^{(n)}}{2}},z_{2}^{(n)},{\frac {z_{2}^{(n)}+z_{3}^{(n)}}{2}}\right\rangle }$ ,

Begründung: (S3,S4,S5)

(S4) (DEF) Definition: Dreiecksweg ${\gamma _{2}^{(n)}}:={\left\langle {\frac {z_{2}^{(n)}+z_{3}^{(n)}}{2}},z_{3}^{(n)},{\frac {z_{1}^{(n)}+z_{3}^{(n)}}{2}}\right\rangle }$ ,
(S5) (DEF) Definition: Dreiecksweg ${\gamma _{3}^{(n)}}:={\left\langle {\frac {z_{1}^{(n)}+z_{3}^{(n)}}{2}},z_{1}^{(n)},{\frac {z_{1}^{(n)}+z_{2}^{(n)}}{2}}\right\rangle }$ ,
(S6) (DEF) Definition: Dreiecksweg ${\gamma _{4}^{(n)}}:={\left\langle {\frac {z_{1}^{(n)}+z_{2}^{(n)}}{2}},{\frac {z_{2}^{(n)}+z_{3}^{(n)}}{2}},{\frac {z_{1}^{(n)}+z_{3}^{(n)}}{2}}\right\rangle }$
(S7) (DEF) Sei ${i}\in {\left\lbrace {1},{2},{3},{4}\right\rbrace }$ der kleinste Index mit $\forall _{{k}\in {\left\lbrace {1},,{2},{3},{4}\right\rbrace }}:{\left|\int _{\gamma _{k}^{(n)}}{f{\left({z}\right)}}{\left.{d}{z}\right.}\right|}\leq {\left|\int _{\gamma _{i}^{(n)}}{f{\left({z}\right)}}{\left.{d}{z}\right.}\right|}$ und $\gamma ^{\left({n}+{1}\right)}:={\gamma _{i}^{(n)}}$

Beweisteil 2: Abschätzungen

(S8) $\Rightarrow$ $\int _{\gamma ^{(n)}}f(z)\,dz=\sum _{k=1}^{4}\int _{\gamma _{k}}^{(n)}f(z)\,dz$
(S9) $\Rightarrow$ ${\left|\int _{\gamma ^{n}}{f{\left({z}\right)}}{\left.{d}{z}\right.}\right|}={\left|{\sum _{{k}={1}}^{4}}\int _{\gamma _{k}^{(n)}}{f{\left({z}\right)}}{\left.{d}{z}\right.}\right|}\leq {\sum _{{k}={1}}^{4}}{\left|\int _{\gamma _{k}^{(n)}}{f{\left({z}\right)}}{\left.{d}{z}\right.}\right|}\leq {4}\cdot {\left|\int _{\gamma _{k}^{(n)}}{f{\left({z}\right)}}{\left.{d}{z}\right.}\right|}$ für alle ${n}\in \mathbb {N}$

Begründung: (S7,WG4,DU)

(S10) $\Rightarrow$ ${0}\leq {\left|\int _{\left\langle {z}_{1},{z}_{2},{z}_{3}\right\rangle }{f{\left({z}\right)}}{d}{z}\right|}={\left|\int _{\gamma ^{(0)}}f(z){\left.{d}{z}\right.}\right|}\leq {4}\cdot {\left|\int _{\gamma ^{\left({1}\right)}}{f{\left({z}\right)}}{\left.{d}{z}\right.}\right|}\leq \ldots \leq {4}^{n}\cdot {\left|\int _{\gamma _{i}^{(n)}}{f{\left({z}\right)}}{\left.{d}{z}\right.}\right|}={4}^{n}\cdot {\left|\int _{\gamma ^{\left({n}+{1}\right)}}{f{\left({z}\right)}}{\left.{d}{z}\right.}\right|}$

Beweisteil 3: Durchmesser der Teildreiecke

(S11) Die geschachtelte Definition der Teildreiecke liefert für alle ${n}\in \mathbb {N}$ : $\Delta {\left({{z}_{1}^{(n)}},{{z}_{2}^{(n)}},{{z}_{3}^{(n)}}\right)}\supset \Delta {\left({{z}_{1}^{\left({n}+{1}\right)}},{{z}_{2}^{\left({n}+{1}\right)}},{{z}_{3}^{\left({n}+{1}\right)}}\right)}$ und

\lim _{n\to \infty }\,{\text{diam}}\left(\Delta {\left({{z}_{1}^{(n)}},{{z}_{2}^{(n)}},{{z}_{3}^{(n)}}\right)}\right)=0

(S12) $\Rightarrow$ $\exists _{{z}_{0}\in {U}}\forall _{{n}\in \mathbb {N} }:{z}_{0}\in \Delta ^{(n)}:=\Delta {\left({{z}_{1}^{(n)}},{{z}_{2}^{(n)}},{{z}_{3}^{(n)}}\right)}$ und ${\left\lbrace {z}_{0}\right\rbrace }=\bigcap _{{n}\in \mathbb {N} }\Delta ^{(n)}$

Beweisteil 4: Holomorphie verwenden (P3)

(S13) Wir vewenden nun die Holomorphie von $f$ in $z_{0}\in U$ für weitere Schritte mit

f(z):=f(z_{0})+f'(z_{0})\cdot (z-z_{0})+r(z)

und

\lim _{z\to z_{0}}{\frac {r(z)}{z-z_{0}}}=0

Begründung: (P3)

(S14) $\Rightarrow$ Die Funktion ${h}:{U}\to \mathbb {C}$ mit $h(z):=f(z_{0})+f'(z_{0})\cdot (z-z_{0})$ besitzt eine Stammfunktion $H(z):=f(z_{0})+f'(z_{0})\cdot {\frac {1}{2}}\cdot (z-z_{0})^{2}$

Begründung: da

h(z)

ein Polynom vom Grad 1 ist.

(S15) $\Rightarrow$ Das Wegintegral über geschlossene Wege $\gamma ^{(n)}$ der Funktion ${h}:{U}\to \mathbb {C}$ ist damit $\int _{\gamma _{k}^{(n)}}{h}{\left({z}\right)}={0}$

Begründung: (SF)

(S16) $\Rightarrow$ Für das Wegintegral über geschlossene Wege $\gamma ^{(n)}$ der Funktion ${f}:{U}\to \mathbb {C}$ gilt $\int _{\gamma _{k}^{(n)}}{f{{\left({z}\right)}{\left.{d}{z}\right.}}}=\int _{\gamma _{k}^{(n)}}{h}{\left({z}\right)}+{r}{\left({z}\right)}{\left.{d}{z}\right.}=\int _{\gamma _{k}^{(n)}}{r}{\left({z}\right)}{\left.{d}{z}\right.}$

Beweisteil 4: Abschätzung des Restglieds $r(z)$

(S17) $\Rightarrow$ Mit $\lim _{z\to z_{0}}{\frac {r(z)}{z-z_{0}}}=0$ gilt: Für alle $\epsilon >{0}$ gibt es ein $\delta >{0}$

|z-z_{0}|<\delta \Rightarrow \left|{\frac {r(z)}{z-z_{0}}}\right|<\epsilon

Begründung:

\epsilon

-

\delta

-Kriterium angewendet auf

g(z):={\frac {r(z)}{z-z_{0}}}

und Stetigkeit von

g

in

z_{0}

(S18) $\Rightarrow$ Für alle $\epsilon >{0}$ gibt es ein $\delta >0$ : $|z-z_{0}|<\delta \Rightarrow |r(z)|<\epsilon \cdot |z-z_{0}|$

0\leq \left|\int _{\left\langle z_{1},z_{2},z_{3}\right\rangle }f(z)\,dz\right|\leq 4^{n}\cdot \left|\int _{\gamma _{k}^{(n)}}f(z)\,dz\right|=4^{n}\cdot \left|\int _{\gamma _{k}^{(n)}}r(z)\,dz\right|\leq 4^{n}\cdot \int _{\gamma _{k}^{(n)}}|r(z)|\,dz\leq 4^{n}\cdot \int _{\gamma _{k}^{(n)}}\epsilon \cdot |z-z_{0}|\,dz

Begründung: (S2)

(S20) Aus der Bedingung $\lim _{n\to \infty }{\text{diam}}\left(\Delta ^{(n)}\right)=0$ existiert für alle $\epsilon >0$ ein $n_{\delta }\in \mathbb {N}$ mit $\Delta ^{(n)}\subseteq {D}_{\delta }(z_{0})$ für alle $n>n_{\delta }$ .
(S21) $\Rightarrow$ $|z-z_{0}|<L\left(\gamma ^{(n)}\right)={\frac {1}{2^{n}}}\cdot L\left(\gamma \right)$ für alle $n\in \mathbb {N}$ und alle $z\in \Delta ^{(n)}$

Begründung: Der Faktor

{\frac {1}{2^{n}}}

entsteht durch die fortgesetzte Halbierung der Seiten der Dreiecke

\Delta ^{(n)}

(S22) Daraus folgt:

0\leq \left|\int _{\langle z_{1},z_{2},z_{3}\rangle }f(z)\,dz\right|\leq 4^{n}\cdot \int _{\gamma _{k}^{(n)}}\epsilon \cdot |z-z_{0}|\,dz\leq 4^{n}\cdot \epsilon \cdot \int _{\gamma _{k}^{(n)}}{\frac {1}{2^{n}}}\cdot {\mathcal {L}}(\gamma )\,dz=4^{n}\cdot \epsilon \cdot {\frac {1}{2^{n}}}\cdot {\mathcal {L}}(\gamma )\underbrace {\leq \int _{\gamma _{k}^{(n)}}1\,dz} _{{\mathcal {L}}(\gamma _{k}^{(n)})}

\leq 4^{n}\cdot \epsilon \cdot {\frac {1}{2^{n}}}\cdot L(\gamma )\cdot {\mathcal {L}}(\gamma _{k}^{(n)})\leq 4^{n}\cdot \epsilon \cdot {\frac {{\mathcal {L}}(\gamma )}{4^{n}}}=\epsilon \cdot {\mathcal {L}}(\gamma )

für alle

\epsilon >0

Begründung: (S19,LIW,IAL)

(C1) $\Rightarrow$ $\int _{\left\langle {z}_{1},{z}_{2},{z}_{3}\right\rangle }{f{\left({z}\right)}}{d}{z}={0}$

Abkürzungen für Begründungen

(DU) $\forall _{a,b\in \mathbb {C} }:|a+b|\leq |a|+|b|$
(DI) Definition: Sei $M\subset {C}$ eine Menge ${\text{diam}}(M):={\text{sup}}\lbrace |b-a|\,:\,a,b\in M\rbrace$
(WE) Definition (Weg): Sei ${U}\subseteq \mathbb {C}$ eine Teilmenge und $a,b\in \mathbb {R}$ mit $a<b$ . Ein Weg $\gamma$ in $U\subseteq \mathbb {C}$ ist eine stetige Abbildung $\gamma :[a,b]\to U$ .
(SPU) Definition (Spur): Sei $\gamma :[a,b]\to U$ eine Weg in ${U}\subseteq \mathbb {C}$ . Die Spur von $\gamma$ ist definiert als: ${\text{Spur}}(\gamma ):=\lbrace \gamma (t)\in \mathbb {C} \,{\mid }\,t\in [a,b]\rbrace$ .
(WZ) Definition (wegzusammenhängend): Sei ${U}\subseteq \mathbb {C}$ eine Teilmenge. ${U}$ heißt wegzusammenhängend, wenn es zu beliebigen Punkt $z_{1},z_{2}\in U$ einen Weg $\gamma :[a,b]\to U$ in $U\subseteq \mathbb {C}$ gibt, mit $\gamma (a)=z_{1}$ , $\gamma (b)=z_{2}$ und ${\text{Spur}}(\gamma )\subseteq U$ .
(GE) Definition (Gebiet): Eine Teilmenge ${G}\subseteq \mathbb {C}$ heißt Gebiet, wenn (1) ${G}$ offen, (2) ${G}\neq \emptyset$ und (3) ${G}$ wegzusammenhängend ist.
(WG1) Definition (Weg glatt): Ein Weg $\gamma :[a,b]\to \mathbb {C}$ heißt glatt, wenn dieser stetig differenzierbar ist.
(UT) Definition (Unterteilung): Sei $[a,b]$ ein Intervall, $n\in \mathbb {N}$ und ${a}={u}_{0}<{\ldots }<{u}_{n}={b}$ . ${\left({u}_{0},\ldots ,{u}_{n}\right)}\in \mathbb {R} ^{n+1}$ heißt dann Unterteilung von ${\left[{a},{b}\right]}$ .
(WG2) Definition (Wegunterteilung): Sei $\gamma :[a,b]\to \mathbb {C}$ ein Weg in ${U}\subseteq \mathbb {C}$ , ${n}\in \mathbb {N}$ , ${\left({u}_{0},\ldots ,{u}_{n}\right)}$ eine Unterteilung von $[a,b]$ , $\gamma _{k}:{\left[{u}_{{k}-{1}},{u}_{k}\right]}\to \mathbb {C}$ für alle ${k}\in {\left\lbrace {1},\ldots ,{n}\right\rbrace }$ ein Weg in ${U}$ . ${\left(\gamma _{1},\ldots ,\gamma _{n}\right)}$ heißt Wegunterteilung von $\gamma$ , wenn gilt $\gamma _{n}{\left({b}\right)}=\gamma {\left({b}\right)}$ und $\forall _{{k}\in {\left\lbrace {1},\ldots ,{n}\right\rbrace }}\forall _{{t}\in {\left[{u}_{{k}-{1}},{u}_{k}\right)}}:\gamma _{k}{\left({t}\right)}=\gamma {\left({t}\right)}\wedge \gamma _{k}{\left({u}_{{k}-{1}}\right)}=\gamma _{{k}-{1}}{\left({u}_{k}\right)}$ .
(WG3) Definition (Integrationsweg/Weg stückweise glatt): Ein Weg $\gamma :{\left[{a},{b}\right]}\to \mathbb {C}$ heißt stückweise glatt, wenn eine Wegunterteilung ${\left(\gamma _{1},\ldots \gamma _{n}\right)}$ aus glatten Wegen $\gamma _{k}$ für alle ${k}\in {\left\lbrace {1},\ldots ,{n}\right\rbrace }$ existiert.
(WG4) Definition (Wegintegral): Sei $f:U\to \mathbb {C}$ eine stetige Funktion und $\gamma :[a,b]\to U$ ein glatter Weg, dann ist das Wegintegral wie folgt definiert: $\int _{\gamma }f:=\int _{\gamma }f(z)\,dz:=\int _{a}^{b}f(\gamma (t))\cdot \gamma '(t)\,dt$ . Ist $\gamma$ nur stückweise glatt bzgl. einer Wegunterteilung $(\gamma _{1},\ldots ,\gamma _{n})$ , dann definiert man $\int _{\gamma }f(z)\,dz:=\sum _{k=1}^{n}\int _{\gamma _{k}}f(z)\,dz$ .
(SF) Satz (Stammfunktion mit geschlossenen Wegen): Besitzt eine stetige Funktion $f:U\to \mathbb {C}$ eine Stammfunktion $F:U\to \mathbb {C}$ , dann gilt für den stückweise glatten Weg $\gamma :[a,b]\to U$ , dass $\int _{\gamma }f(z)\,dz=F(b)-F(a)$ gilt.
(LIW) Länge des Integrationsweges: Sei $\gamma :{\left[{a},{b}\right]}\to \mathbb {C}$ ein glatter Weg, dann ist die ${\mathcal {L}}(\gamma )$ wie folgt definiert

{\mathcal {L}}(\gamma ):=\int _{a}^{b}|\gamma '(t)|\,dt

.

Ist

\gamma :{\left[{a},{b}\right]}\to \mathbb {C}

allgemein ein Integrationsweg mit der Wegunterteilung

{\left(\gamma _{1},\ldots \gamma _{n}\right)}

aus glatten Wegen

\gamma _{k}

, so ist

{\mathcal {L}}(\gamma )

als Summe der Länge der glatten Wege

\gamma _{k}

definiert, also:

{\mathcal {L}}(\gamma ):=\sum _{k=1}^{n}{\mathcal {L}}(\gamma _{k})

(IAL) Integralabschätzung über die Länge des Integrationsweges: $\gamma :{\left[{a},{b}\right]}\to \mathbb {G}$ ein Integrationsweg auf dem Gebiet $G\subseteq \mathbb {C}$ , dann gilt für eine auf ${\text{Spur}}(\gamma )$ stetigen Funktion folgende Abschätzung:

\left|\int _{\gamma }f(z)\,dz\right|\leq \max _{z\in {\text{Spur}}(\gamma )}|f(z)|\cdot {\mathcal {L}}(\gamma )

Literatur

Eberhard Freitag & Rolf Busam: Funktionentheorie 1, Springer-Verlag, Berlin

Siehe auch

Kurs:Funktionentheorie/Lemma von Goursat - Kurzform
Integrationsweg

Seiten-Information

Diese Seite wurde auf Basis der folgenden Wikipedia-Quelle erstellt:

This article is issued from Wikiversity. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.