Rekursionsbäume

Spezialfall Divide and Conquer

Bei MergeSort sehen die Divide and Conquer Schritte wie folgt aus:

1. Divide: Zerteile eine Folge mit n Elementen in zwei Folgen mit je n/2 Elementen.
2. Conquer: Wenn die resultierende Folge 1 oder 0 Elemente enthält,dann ist sie sortiert. Ansonsten wende MergeSort rekursiv an.
3. Combine: Mische die zwei sortierten Teilfolgen.

${\displaystyle T(n):=\left\{{\begin{array}{ll}\Theta (1)&{\text{für }}(n\leq 1)\\D(n)+\alpha \cdot T(n/b)+C(n)&{\text{sonst}}\end{array}}\right.}$

public List mergeSort(List f) {
  if (f.size() <= 1) {
    return f;
  } else {
    int m = f.size() / 2;
    List left = mergeSort(f.subList(0,m));
    List right = mergeSort(f.subList(m,f.size());
    return merge(left, right);
  }
}

${\displaystyle T(n):=\left\{{\begin{array}{ll}\Theta (1)&{\text{für }}(n\leq 1)\\2\cdot T(n/2)+\Theta (n)&{\text{sonst}}\end{array}}\right.}$

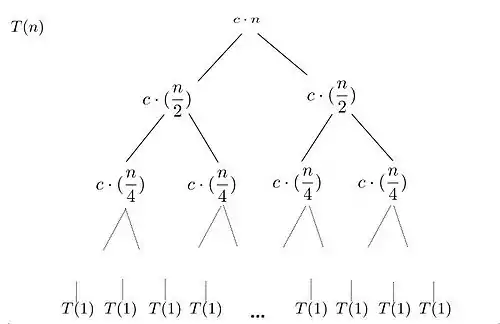
Herleitung des Aufwandes

Die Grundidee ist das wiederholte Einsetzen der Rekursionsgleichung in sich selbst als Baum dargestellt. Das Ziel ist ein Muster zu erkennen. Bei einem Rekursionsbaum beschreibt ein Knoten die Kosten eines Teilproblems. Die Blätter sind die Kosten der Basis fällt T(0) und T(1). Der Aufwand bestimmt sich aus der Summe über alle Ebenen.

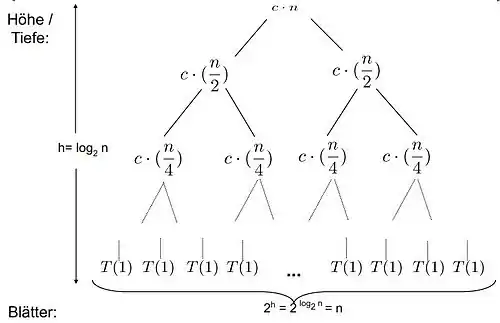
1. Ebene ${\displaystyle c\cdot n}$

2. Ebene ${\displaystyle 2\cdot {\frac {1}{2}}\cdot c\cdot n}$

3. Ebene ${\displaystyle 4\cdot {\frac {1}{4}}\cdot c\cdot n}$

....

n. Ebene ${\displaystyle \Theta (1)\cdot n=\Theta (n)}$

Der Aufwand berechnet sich nun wie folgt:

${\displaystyle T(n)=c\cdot n+2\cdot {\frac {1}{2}}\cdot c\cdot n+4\cdot {\frac {1}{4}}\cdot c\cdot n+2^{log_{2}n-1}\cdot {\frac {1}{2^{log_{2}n-1}}}\cdot c\cdot n+\Theta (n)}$

${\displaystyle =\sum _{i=0}^{log_{2}n-1}c\cdot n+\Theta (n)}$

${\displaystyle =c\cdot n\cdot \sum _{i=0}^{log_{2}n-1}1+\Theta (n)}$

${\displaystyle =c\cdot n\cdot log_{2}n+\Theta (n)}$

${\displaystyle =\Theta (n\cdot log_{2}n)+\Theta (n)=\Theta (n\cdot log_{2}n)}$

Allgemein bestimmt sich der Aufwand T(n) durch die Summe des Aufwands je Ebene und des Aufwands der Blattebene.

Bezogen auf den gegebenen Rekursionsbaum wäre das ${\displaystyle T(n)=3\cdot T(n/4)+c\cdot n^{2}}$

Literatur

Da die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 8.3 zu finden.