Numerische Methode

Potenzial zwischen Argon-Atomen, Lennard-Jones-Näherung

Morse-Potenzial zwischen Kupfer-Atomen

Dieser Abschnitt tastet sich numerisch an die Schrödinger-Gleichung heran in einer Dimension und findet Lösungen im Potenzialtopf. Das Beispiel Morse-Potenzial lässt sich zum besseren Vergleich auch analytisch lösen. Ein Python-Skript soll zeigen, dass mit rustikaler Numerik recht gute Ergebnisse herauskommen -- bei niedrigen Energien mit der eindimensionalen Schrödinger-Gleichung, wo z.B. die WKB-Näherung zu schlecht wäre.

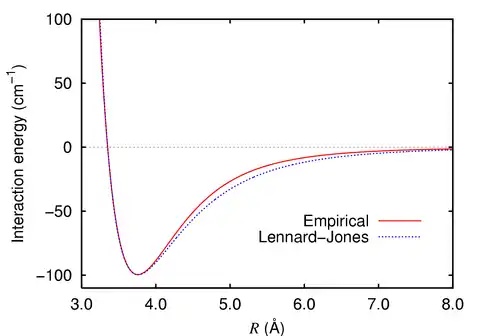
Ein radiales Potenzialmodell für die Anziehung zwischen Atomen oder Molekülen mit einem abstoßendem Kernbereich ist das Lennard-Jones-Potenzial mit den zwei Parametern E,s:

${\displaystyle V_{LJ}(r)\;:\quad V_{LJ}(r)/E=4[(s/r)^{12}-(s/r)^{6}]}$

Es ist negativ für r>s und positiv für r<s.
Sein Minimum (-E) liegt bei ${\displaystyle r=2^{1/6}s.}$

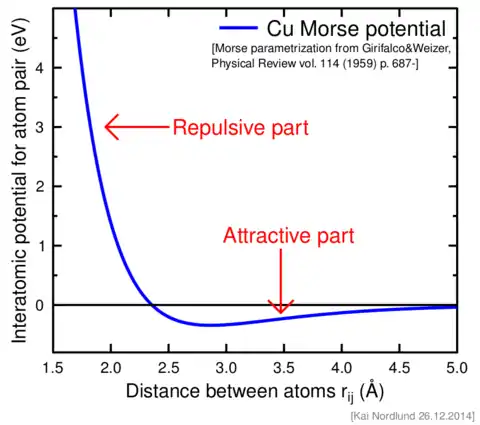
Hier soll mit der ähnlichen Morse-Potenzialfunktion gerechnet werden:

${\displaystyle p(x)=\exp(-2x/b)-2\exp(-x/b)}$.

Schrödinger-Gleichung: ${\displaystyle (-\hbar ^{2}/(2m))\cdot \phi ''+Vp(x)\phi =E\phi }$.

Der Potenzialtopf ist sehr unsymmetrisch, er steigt bei negativem ${\displaystyle x<(-b)}$ steil an, hat ein Minimum (-V) bei x=0 und flacht für großes ${\displaystyle x>b}$ gegen Null ab. Die Länge b misst die Ausdehnung des Topfes, die Konstante V seine Tiefe. Ein solches Potenzial simuliert in etwa die Kraft, mit der zwei Atomkerne in einem Molekül gebunden sind. Es kann ein typisches Spektrum der Vibrationen des Moleküls darstellen.

Die X-Variable wird zu dimensionslosem y skaliert:

${\displaystyle y=x/b;\;d/dy=b(d/dx);\;p(y)=\exp(-2y)-2\exp(-y)}$.

Gleichung: ${\displaystyle [-\hbar ^{2}b^{2}/(2m)]\phi ''(y)+Vp(y)\phi =E\phi }$.

Energie-Skalierung, ebenfalls zu dimensionslosen Werten:

${\displaystyle ({\bar {E}},{\bar {V}})=(E,V)\cdot 2m/(\hbar ^{2}b^{2})}$

Ergibt einfach, mit unterdrückten Strichen: ${\displaystyle -\phi ''=(E-Vp(y))\phi }$.

Das Potenzial-Minimum ist (-V) bei y=0. Laut Theorie sind die Niveaus:

${\displaystyle E_{n}=-({\sqrt {V}}-(n+{\tfrac {1}{2}}))^{2};\quad {\sqrt {-E_{n}}}=[{\sqrt {V}}-(n+{\tfrac {1}{2}})]\quad (n=0...N)}$

Mit dem Beispiel V=200 ergeben sich 14 Energie-Niveaus n=0...13.

Das Skript löst die Schrödinger-Gleichung im Morse-Potenzial und findet eine Serie der ersten 8 gebundenen Zustände. Die Wellenfunktionen und die Energieniveaus werden als SVG-Grafik ausgegeben. Trotz der langsamen Sprache Python und der lahmen Technik von numerischer Integration tausender Probeschüsse ist das Ergebnis in ein paar Sekunden fertig. Im ersten Durchgang wird für ein Raster von 50 Punkten der Energie im Potenzialtopf je eine Probewelle berechnet.

Angenäherte Differenzgleichung: die Gleichung ${\displaystyle f''=g(x,f)}$ wird numerisch auf einem Gitter von gleich entfernten x-Punkten zur Differenzgleichung

${\displaystyle (f[x+d]+f[x-d]-2f[x])/d^{2}=g(x,f[x])}$.

Sind zwei Anfangswerte bekannt, kann eine Kurve f() Schritt für Schritt 'integriert' werden:

${\displaystyle f[x+d]=d^{2}\cdot g(x,f[x])+(2f[x]-f[x-d])}$.

Probewelle: An den Rändern des Topfes, das heißt an den klassischen Umkehrpunkten, wird zuerst je eine (mindestens exponentiell) abfallende Lösung in die Potenzialmauer hinein iteriert. Dann wird die oszillierende Welle f von Rand zu Rand geführt, mit stetig-differenzierbarer Anfangsbedingung links. Am rechten Punkt wird der Sprung der relativen Steigung ${\displaystyle f'(x)/f(x)}$ bezüglich der Randlösung vermerkt. Wäre die Welle ein erlaubter Zustand, dann wäre dieser Fehler Null. Gleichzeitig werden auch die Knoten (Nulldurchgänge) der Welle im Topf gezählt.

Im zweiten Durchlauf werden benachbarte Paare aus dem Raster gezogen, die zur gleichen Knotenzahl gehüren, aber zwischen denen sich das Vorzeichen beim Steigungs-Knacks umkehrt. Ein solches Paar von Energie-Niveaus ist dann eine Klammer, zwischen der sich ein erlaubtes Niveau mit Knotenzahl N befindet. Mit Dichotomie und einer Iteration von Probewellen wird die Eigenfunktion und der Eigenwert der Energie ermittelt. Genauer, die Nullstelle der Steigungs- Unstetigkeit. Spontan ergeben sich N=0,1...7 als Serie von Quantenzuständen.

Die Fehler der Energie, verglichen mit der Theorie, sind kleiner als 0,1%. Die höchsten Niveaus N=8 bis 13 werden nicht erkannt. Das Raster nahe beim Niveau Null müsste dazu feiner gewählt werden. Besser noch wäre, beide Durchläufe zu vereinen und das Such-Raster adaptiv nach den Energie-Abständen zu justieren. Vielleicht adaptive Schrittweiten auch bei den unzähligen Summierungen der Differenzengleichung, das Näherungsverfahren für die Integration der Differenzialgleichung?

Theoretische Berechnung

Löse die Gleichung: ${\displaystyle -\phi ''(z)+Vu(z)\phi =E\phi$ ;\;u(z)=e^{-2z}-2e^{-z}} .

Die Strategie: schalte um zu bequemeren Variablen, im Definitionsbereich von z zu t und im Wertebereich von ${\displaystyle \phi (z)}$ zu ${\displaystyle w(t)}$. Die transformierte Differenzialgleichung in {w,t} sollte lösbar sein.

Ansatz: ${\displaystyle t=t(z)=fe^{-z}\quad {\text{und}}\quad w(t)=e^{at}t^{b}\phi (z)}$.

Die drei freien Parameter ${\displaystyle a,b,f}$ werden später getrimmt. Ableitungen nach z werden mit Strichen, solche nach t mit Punkten markiert.

${\displaystyle (dt/dz)=-fe^{-z}=-t;\;(d^{2}t/dz^{2})=fe^{-z}=t;\;e^{-z}=(t/f);\;z=-\ln(t/f)}$

${\displaystyle w'=(dw/dz)=at'w+bw(t'/t)+w(\phi '/\phi )=(-at-b)w+(\phi '/\phi )w}$

${\displaystyle w''=[-at-b+(\phi '/\phi )]w'+[-at'+(\phi ''\phi -\phi '^{2})/\phi ^{2}]w}$

(vorgemerkt)${\displaystyle \quad w'=-{\dot {w}}t;\;w''=(d/dz)(-{\dot {w}}t)={\ddot {w}}t^{2}+{\dot {w}}t}$

Mit ${\displaystyle (\phi '/\phi )=(w'/w)+(at+b)\quad {\text{und}}\quad (\phi ''/\phi )=Vu(t)-E=:P(t)}$, das ein Polynom der Ordnung 2 in t ist:

${\displaystyle w''=w'^{2}/w+w[at+P(t)-((w'/w)+(at+b))^{2}]}$

${\displaystyle w''=({\dot {w}}^{2}t^{2})/w+w[at+P(t)-((-{\dot {w}}t/w)+(at+b))^{2}]}$

${\displaystyle w''=w[at+P(t)-(at+b)^{2}+2(at+b)t({\dot {w}}/w)],\quad }$ Term in ${\displaystyle {\dot {w}}^{2}}$ entfällt.

Mit ${\displaystyle w''={\ddot {w}}t^{2}+{\dot {w}}t}$ wird schließlich die Gleichung sauber in w und t:

${\displaystyle {\ddot {w}}t^{2}+{\dot {w}}[t-2(at+b)t]+w[(at+b)^{2}-at-P(t)]=0}$

Nun ist ${\displaystyle P(t)=V((t/f)^{2}-2(t/f))-E}$. Mit der Wahl ${\displaystyle b^{2}+E=0}$ kann der inhomogene Term entfallen und der Rest durch t geteilt werden. Daher bleibt:

${\displaystyle {\ddot {w}}t+{\dot {w}}[1-2(at+b)]+w[(at+v)^{2}-at-Vt/f^{2}+2V/f]=0}$

Es gibt Licht am Ende des Tunnels.

Weitere Wahl: ${\displaystyle a^{2}-V/f^{2}=0}$ entfernt den Faktor von ${\displaystyle t^{2}}$.

Dritte Wahl : ${\displaystyle 2a=1}$ entfernt auch den Faktor von t im w-Term. Also a=1/2.

${\displaystyle {\ddot {w}}t+{\dot {w}}[1+b-t]+w[b-a+2fa^{2}]=0;\;f=\pm 2{\sqrt {V}}}$.

Was hier bleibt, ist die Differenzialgleichung der Kummer-Funktionen F.

${\displaystyle F(A,B;z)\;}$ löst die Gleichung ${\displaystyle \;zF''+(B-z)F'-AF=0}$.

Wenn dazu noch A eine nicht-positive Ganzzahl (-n) ist, ist die Lösung F ein Polynom in z.

Im Abschnitt Potenzial-Streuung steht etwas mehr zu den Kummer-Funktionen.

In der Hoffnung, dass mit den Polynomen zu quanteln ist, rechnet man (n) aus:

${\displaystyle f=\pm {\sqrt {V}}/a;\quad n=b-a-2fa^{2}=(\pm {\sqrt {-E}})-(1/2)+(\pm {\sqrt {V}})}$

Die Physik sagt: E ist eine negative Bindungs-Energie zwischen -V und 0.

Die sinnvollen Vorzeichen sind daher: ${\displaystyle b=-{\sqrt {-E}}\quad {\text{und}}\quad f=2{\sqrt {V}}}$.

Erlaubte Energie-Niveaus: ${\displaystyle {\sqrt {-E_{n}}}={\sqrt {V}}-(n+{\tfrac {1}{2}});\;n=0,1,2...}$

Die Energien sind negativ und die Serie der ${\displaystyle E_{n}}$ ist endlich.

Sind die Wellenfunktionen ${\displaystyle \phi (z)=w(t)e^{-at}t^{-b}}$ nun überhaupt gutartig, wobei ${\displaystyle w(t)=F(t)}$ ein Polynom ist?

${\displaystyle t=fe^{-z};\;z=-log(t/f);\;a=1/2;\;b=-{\sqrt {-E}};\;f=2{\sqrt {V}}>0}$.

${\displaystyle \phi (z)=F(t)e^{-t/2}t^{\sqrt {-E}}\;}$ mit positiver Potenz von t.

Für ${\displaystyle z\to \infty ,\;t\to 0\;\Rightarrow \phi \to F(t)t^{\sqrt {-E}}=0}$

Für ${\displaystyle z\to -\infty ,\;t\to \infty \;\Rightarrow \phi \propto e^{-t/2}\to 0}$.

Tatsächlich sind annehmbare zeitunabhängige Schrödinger-Lösungen gefunden.

Skript

from math import exp,sqrt,log
def div(p,q) : return int(p/q)
def pot(x) : return exp(-2*x)-2*exp(-x)

def shoot(x,dx,f,df,xlim, v0,erg) : # decay tails in both dirs
  xa=x;xb=x+dx;xc=xb+dx; ya=f;yb=f+df; steps=0; smax=1000; ymax=3*f; node=0
  smax= int(abs((xlim-x)/dx)); ix=0; done=False; zb=abs(yb); data=[xa,ya]
  while not done : # f"= (e-u)f = (yc+ya-2yb)/dx^2 = (erg-u(xb))*yb
    z= -dx*dx*yb*(erg-v0*pot(xb)); yc= z+2*yb-ya;xc=xb+dx; zc=abs(yc); steps+=1
    if (yc*yb)<0 : node+=1
    done= (steps>smax)or(zc>zb) or (yc<0)or(yc>ymax); ix+=1
    if not done : xa=xb;ya=yb; xb=xc;yb=yc; zb=zc; data += [xa,ya] 
    if done and (steps<smax) : yc= yc*smax/(steps+0.0)  
  return yc,node,ix, data 

def waveshot(x,f,df, y, v0,erg) : # start f(x), df=derivative, oscillates
  steps=0; smax=1000; node=0; dx=(y-x)/(smax+0.0); dfdx=df*dx
  xa=x-dx;xb=x; ya=f-dfdx; yb=f; ix=0; noisy=False; data=[xb,yb]
  while (ix<smax) : # f"= (u-e)f = (yc+ya-2yb)/dx^2 = (u(xb)-erg)*yb
    z= dx*dx*yb*(v0*pot(xb)-erg); yc= z+2*yb-ya; xc=xb+dx; ix +=1
    if (yc*yb)<0 : node+=1
    xa=xb;ya=yb; xb=xc;yb=yc; data += [xb,yb]
    if noisy and (ix%50)==0 : print('z='+str(z)) # should be wavy
  return xb,yb,(yb-ya),dx, node, data 

def bestshot(x,dx,f, v0,erg) : #  try to get optimal decay to zero
  df=0; targ=0; dfhi=0; dflo=-f; noisy=0 # zhi=2*f; zlo=-0.1*f; 
  zbefore=10; i=0; busy=True; zmi=targ-0.1; zmx=targ+0.1;zhi=zmx;zlo=zmi
  while busy :
    z,node,ix,data = shoot(x,dx,f,df, 5.0, v0,erg);
    if noisy>=2 : print(str([z,node,ix,df]))
    if z>targ : dfhi=df;zhi=z 
    else : dflo=df;zlo=z
    df=0.5*(dfhi+dflo);
    if (zlo>zmi)and(zlo<zhi)and(zhi<zmx) :
      df=dflo+(targ-zlo)*(dfhi-dflo)/(zhi-zlo)
    i+=1; busy= (abs(z-zbefore)>1e-8); zbefore=z
  if noisy>0 : print('Shotloop i,df,dx,z='+str([i,df,dx,z])) 
  return df,dx, data

def schroedinger(erg,v0): # data 3 arrays of xy pairs, queue-wave-queue.
  dx=0.01; xa=0; xb=0; fa=1; fb=1; noisy=False; data=[[]]*3
  while erg> (v0*pot(xa)) : xa += dx
  while erg> (v0*pot(xb)) : xb -= dx 
  if noisy : print('erg,v0,xb,xa='+str([erg,v0,xb,xa]))
  dfa,dxa,data[2] = bestshot(xa,dx,fa, v0,erg);
  dfb,dxb,data[0] = bestshot(xb,-dx,fb, v0,erg); 
  xx,yy,dy,dxx, node, data[1] = waveshot(xb,fb,dfb/dxb, xa, v0,erg)
  if noisy : print('waveshot to '+str([xx,yy,dy,node]))
  ta=dfa/dxa/fa; ht=dy/dxx/yy # compare target to hit
  # print('Target and hit slopes: '+str([ta,ht]))
  return node, ht/ta, data

def pairflip(d) :
  j=len(d); k=j-2;i=0
  while (i<k) :
    x=d[i];y=d[i+1];d[i]=d[k];d[i+1]=d[k+1];d[k]=x;d[k+1]=y
    i=i+2; k=k-2 

def squareint(d) : # square-integral
  j=len(d); i=0; sum=0
  while i<(j-3) :
    dx= d[i+2]-d[i]; y=d[i+1];z=d[i+3]; sum += 0.5*dx*(y*y+z*z); i+=2
  return sum

def rescale(d,f) : # return bounds too
  j=len(d); i=0; xmin=1e12;xmax=-xmin;ymin=xmin;ymax=xmax
  while i<j :
    x=d[i]; y= d[i+1]*f; d[i+1]=y; i=i+2
    xmin= x if(x<xmin) else xmin; xmax= x if (x>xmax) else xmax
    ymin= y if(y<ymin) else ymin; ymax= y if (y>ymax) else ymax
  return xmin,ymin, xmax,ymax

def findwave(v,scan,ifd,node,plot) : #bracket search for solution in scan table
  ea,na,ra= tuple(scan[ifd]); eb,nb,rb= tuple(scan[ifd+1])
  ra= ra-1; rb=rb-1; k=0; ec=0.5*(ea+eb); r=1; ed=1
  while (k<20)and(abs(r)>1e-5) :
    print('k, r,ea,eb,ec,ed='+str([k,r,ea,eb,ec,ed]))
    nn,r,data = schroedinger(ec,v); r= r-1; k+=1 # r seems negative always!?
    if (r*ra)>0 : ra=r;ea=ec
    else : rb=r; eb=ec
    ed= ea+(-ra)*(eb-ea)/(rb-ra) # better target zero?
    if ((ed-ea)*(ed-eb))<0 : ec=ed
    else : ec= 0.5*(ea+eb)
  print('Data ranges:') # reverse first list, y-rescale last
  pairflip(data[0]); d=data[1]; j=len(d); yb=d[j-1]; sum=0
  rescale(data[2],yb)
  for k in range(len(data)) :
    d=data[k]; j= len(d); xa,ya,xb,yb=d[0],d[1],d[j-2],d[j-1]
    print('j xy xy'+str([j,xa,ya,xb,yb]))
    s=squareint(d); print('  SquareInt='+str(s)); sum+=s
  norm=sqrt(sum); print('Norm='+str(norm)) # divide all stuff by this one
  for k in range(3) :
    xa,ya,xb,yb= rescale(data[k],1.0/norm); print(str([xa,ya,xb,yb]))  
    if k==0 : xmin,ymin,xmax,ymax= xa,ya,xb,yb
    else :
      xmin=min(xmin,xa);ymin=min(ymin,ya);xmax=max(xmax,xb);ymax=max(ymax,yb)
  if plot : waveplot('morsew'+str(node), node, ec, xmin,ymin,xmax,ymax,data)
  return([ec, node, xmin,ymin,xmax,ymax,data])

def multiplot(d) :
  n=len(d); xmin=1e12;xmax=-xmin;ymin=xmin;ymax=xmax
  txt=[]; fn='morse'; ix=[0]*(1+3*n)
  for i in range(n) :
    j=1+3*i;k=i+1; ix[j],ix[j+1],ix[j+2]= k,k,k # color index
    ec, node, xa,ya,xb,yb,dt = tuple(d[i])
    xmin= xa if(xa<xmin) else xmin; xmax= xb if (xb>xmax) else xmax
    ymin= ya if(ya<ymin) else ymin; ymax= yb if (yb>ymax) else ymax
  xyf=[ xmin,ymin, xmax,ymin, xmax,ymax, xmin,ymax, xmin,ymin]; xys=[xyf]
  for i in range(n) :
    ec, node, xa,ya,xb,yb,dt = tuple(d[i]); xys+=[dt[0],dt[1],dt[2]]
    txt+= ['E'+str(node)+'= '+str(aprx(ec))]
  xs,fx,xpix= xmin, 750/(xmax-xmin),25 # scale user units, min in pixels
  ys,fy,ypix= ymin,-550/(ymax-ymin),575 ; scale=(xs,fx,xpix, ys,fy,ypix)
  colo=['#aaa','#00a','#077','#0a0','#770','#a00','#707','#0ff','#f0f']
  sd=svgdump(); buf=sd.plotbegin(800,600,1); i=0; dy=(ymax-ymin)/20.0
  for j in range(len(txt)) :
    buf += label(sd,scale, txt[j], 0.2*xmin+0.8*xmax,ymax-dy-j*dy)
  for t in xys : buf += curve(sd,scale, t, fill=colo[ix[i]]); i+=1
  g=open(fn+'.svg','w'); g.write(buf+sd.plotend()); g.close()

def energytheory(v,d) : # compare energy, theory versus numerical
  n=0; ok=True; ec=0; ld=len(d)
  while ok : 
    if n<ld : ec, node, xa,ya,xb,yb,dt = tuple(d[n])
    z= sqrt(v)-(n+0.5); ok= z>=0
    if ok : y=-z*z; print(str([n,y,ec])); n+=1; ec=0

def test() : # stationary schroedinger equ numerics, 8 energy levels found
  v=200; n=50; scan=[[]]*n; waves=[] # scan 50 energy levels
  for i in range(1,n) : # scan for node numbers and slope defects
    erg= -v + i*v/(n+0.0); node,rsl, data= schroedinger(erg,v)
    scan[i]=[erg,node,rsl]
    print('*** Erg,nodes,rslope='+str(scan[i]))
  for i in range(1,n-1) :
    ea,na,ra= tuple(scan[i]); eb,nb,rb= tuple(scan[i+1])
    found= (na==nb)and ((ra-1.0)*(rb-1.0)<0) # cross sloperatio=1
    if found :
      print('found i='+str(i)+',nodes='+str(na)); ifd=i;node=na
      wave= findwave(v,scan,ifd,node, False); waves += [wave]
  print('Number of waves='+str(len(waves))+'. Theory vs. Numerical:');
  multiplot(waves); energytheory(v,waves)

###### plot

class svgdump :
  def plotbegin(sd, w,h,f) : # args: width height zoomfactor
    W=str(w); H=str(h); u=''; fw=str(f*w); fh=str(f*h)
    s=( '<?xml version="1.0" encoding="UTF-8" standalone="no"?>\n'+
     '<!DOCTYPE svg>\n'+
     '<svg xmlns="http://www.w3.org/2000/svg"\n'+
     '  xmlns:xlink="http://www.w3.org/1999/xlink"\n'+
     '  width="'+W+'" height="'+H+'" viewBox="0 0 '+fw+' '+fh+'">\n')
    return s

  def plotend(sd) : return '</svg>\n'
  def move(sd,x,y) : return 'M'+str(x)+','+str(y)
  def line(sd,x,y) : return 'L'+str(x)+','+str(y)
      
  def labl(sd,s,x,y, size=14,fill='#000') :
    f=' font-family="Arial"'
    t='<tspan x="'+str(x)+'" y="'+str(y)+'">'+s+'</tspan>'; fsz= str(size)
    return ('<text fill="'+fill+'"'+f+' font-size="'+fsz+'px">'+t+'</text>\n')

  def path(sd,w,s,lc='#000') : # path w=with lc=linecolor
    t='<path fill="none" stroke="'+lc+'" stroke-width="'+str(w)+'" '
    t+= ' stroke-linecap="round" ' 
    return t + 'd="\n'+s+'" />\n'

# end class svgdump

def aprx(x) : # 3-digit approximation
  y= (-x) if(x<0) else x; z= int(1e3*y+1e-3); z= (-z) if (x<0) else z
  return z/1000.0

def curve(sd,scale,xy, fill='#000', width=1) :
  (xs,fx,xmin, ys,fy,ymin) = scale; s=''; n= div(len(xy),2) 
  for i in range(n) : 
    x= aprx(xmin+fx*(xy[2*i]-xs)); y= aprx(ymin+fy*(xy[2*i+1]-ys))
    s+= sd.move(x,y) if(i==0) else sd.line(x,y)
  return sd.path(width,s,lc=fill)

def label(sd,scale,txt,tx,ty) : # tx,ty plot coordinates not pixels
  (xs,fx,xmin, ys,fy,ymin) = scale 
  x= aprx(xmin+fx*(tx-xs)); y= aprx(ymin+fy*(ty-ys))
  return sd.labl(txt,x,y)

######## main program #####
test()

### optional 

def waveplot(fn, lvl, erg, xa,ya,xb,yb,data) :
  txt=['Wavefunct Level '+str(lvl)+' Energy '+str(aprx(erg)),]
  xyf=[ xa,ya, xb,ya, xb,yb, xa,yb, xa,ya ] # frame
  xys=[xyf,data[0],data[1],data[2]]
  xs,fx,xpix= xa, 750/(xb-xa),25 # scale user units, min in pixels
  ys,fy,ypix= ya,-550/(yb-ya),575 ; scale=(xs,fx,xpix, ys,fy,ypix)
  colo=['#777','#00a','#077','#0a0','#770','#a00']
  sd=svgdump(); buf=sd.plotbegin(800,600,1); i=0; dy=(yb-ya)/20.0
  for j in range(len(txt)) :
    buf += label(sd,scale, txt[j], (xa+xb)*0.5,yb-dy-j*dy)
  # for j in range(len(lbl)) :
  #  buf += label(sd,scale, lbl[j], log(fg[j]),yb)
  for t in xys : buf += curve(sd,scale, t, fill=colo[i%7]); i +=1
  g=open(fn+'.svg','w'); g.write(buf+sd.plotend()); g.close()

Alkali-Atom

Beim Wasserstoff-Atom bilden die radialen Schrödinger-Lösungen im zentralen Coulomb-Potenzial Folgen um Laguerre-Polynome herum. Sie sind 'gequantelt' mit zwei ganzzahligen Indizes, worin die Hauptquantenzahl n und die Drehimpuls-Zahl l vorkommen. Wegen der besondere Symmetrie des Potenzials sind die stationären Niveaus stark entartet -- zu gegebenem n haben l=0,1,...n-1 die selbe Bindungsenergie.

Die Alkali-Atome Li bis Cs sind dem Wasserstoff darin ähnlich, dass ein einzelnes Elektron-Niveau sich von den anderen abhebt und in einem effektiven Zentralpotenzial der restlichen Elektronenwolken angenähert beschrieben werden kann. Das Leuchtelektron hat einen deutlichen Energie-Abstand zu den anderen Niveaus, die nach dem Pauli-Prinzip vorher dran kamen und eine stabile, wenig reaktionsfreudige Edelgas-Konfiguration belegen.

Ein Modell dieses effektiven radialen Potenzials soll kurz besprochen werden. Zur Anziehung durch den Atomkern kommt eine Abstoßung durch die inneren Elektronen. Die radiale Differenzialgleichung ist immer noch geschlossen lösbar, mit Hilfe von Modifizierten Laguerre-Polynomen. Die Entartung von ${\displaystyle (n,l)}$ Paaren wird aber aufgehoben.

Der Atomrumpf soll mit zwei dimensionslosen Parametern auskommen, nennen wir sie U und C. Statt der Kernladungszahl Z soll der effektive Coulomb-Anteil, also der in ${\displaystyle (1/r)}$, eine viel kleinere Anziehung (Z-U) haben. Der abstoßende Anteil soll mit ${\displaystyle (1/r^{2})}$ stark abfallen und einen empirischen Faktor C bekommen. Es ist zu prüfen, ob ein Paar ${\displaystyle \{U,C\}}$ beispielsweise einen Bereich des Natrium-Spektrums gut annähert oder ob die Werte noch feiner variiert werden müssen, ob also ein Fit mit mehr als 2 Parametern benötigt wird.

Zuerst mag man die Differenzialgleichung dimensionslos umschreiben, was allgemein für numerische Berechnungen Vorteile bringt. Die Länge wird skaliert in Bezug auf den Bohr-Radius ${\displaystyle a={\frac {\hbar ^{2}}{2m}}{\frac {4\pi \epsilon _{0}}{e^{2}}}}$. Die Energie wird ausgedrückt relativ zur Wasserstoff-Ionisierungsenergie

${\displaystyle E_{0}={\frac {\hbar ^{2}}{2ma^{2}}}}$. Damit ist ${\displaystyle {\frac {\hbar ^{2}}{2m}}=E_{0}a^{2}.\quad E_{0}=}$ 13,6 eV; a=0,0529 nm.

Vernachlässigt wird, die Vielteilchen-Gleichung in Schwerpunktskoordinaten und Relativkoordinaten von Rumpf und Leuchtelektron zu separieren und statt der Elektron-Masse eine reduzierte Masse einzusetzen. Vernachlässigt wird auch der Elektron-Spin, der spinorwertige Winkelfunktionen ${\displaystyle Y_{j;lm}}$ an Stelle der skalaren ${\displaystyle Y_{lm}}$ erfordern würde. Der Spin brächte darüber hinaus eine Feinstruktur ein mit Spin-Bahn-Kopplungsterm im Hamilton-Operator.

Potenzialmodell: ${\displaystyle V={\frac {-(Z-U)q^{2}}{4\pi \epsilon _{0}r}}+{\frac {\hbar ^{2}}{2m}}{\frac {C}{r^{2}}}={\frac {-(Z-U)\hbar ^{2}}{amr}}+{\frac {\hbar ^{2}C}{2mr^{2}}}}$

${\displaystyle {\frac {V}{E_{0}}}=-(Z-U){\frac {2a}{r}}+C{\frac {a^{2}}{r^{2}}};\quad r=|{\vec {x}}|}$

Energie-Niveaus ${\displaystyle F:=(E/E_{0})}$ kommen aus der Eigenwert-Gleichung

${\displaystyle \left[-\nabla ^{2}a^{2}-{\frac {(Z-U)(2a)}{r}}-{\frac {Ca^{2}}{r^{2}}}-F\right]\Psi =0}$

Mit skaliertem Radius ${\displaystyle s=(r/a);\;{\vec {s}}={\vec {x}}/a}$ und ${\displaystyle (d/dr)=a(d/ds)}$:

${\displaystyle \left[-\nabla _{s}^{2}-{\frac {2(Z-U)}{s}}-{\frac {C}{s^{2}}}-F\right]\Psi =0}$

Ansatz: ${\displaystyle \Psi =Y_{lm}(\theta ,\phi )u(s)}$.

Radialgleichung: ${\displaystyle [{\frac {d^{2}}{ds^{2}}}+{\frac {2}{s}}{\frac {d}{ds}}-{\frac {l(l+1)}{s^{2}}}]u(s)+[{\frac {2(Z-U)}{s}}-{\frac {C}{s^{2}}}+F]u(s)=0}$

Nach einem Muster, das schon beim Wasserstoff-Atom geholfen hat, wird noch einmal die Radius-variable skaliert ${\displaystyle x=s/b}$. Und von der Funktion u werden ein Potenz-Faktor und ein Exponential-Faktor abgespalten:

${\displaystyle u(s)=R(x)x^{\lambda }\exp(-x/\mu )}$.

Als beste Option kommt folgendes heraus, um die Eigenwerte F<0 einzukreisen:

${\displaystyle x=2s{\sqrt {-F/E_{0}}};\;u=R(x)x^{\lambda }\exp(-x/2)}$

Damit ergibt sich folgende Differenzialgleichung für ${\displaystyle R(x)}$:

${\displaystyle \left[x{\frac {d^{2}}{dx^{2}}}+(2\lambda +2-x){\frac {d}{dx}}+{\frac {\eta }{x}}+\nu \right]R(x)=0;\quad \eta$ :=\lambda (\lambda +1)-l(l+1)-C;\quad \nu :={\sqrt {-E_{0}/F}}(Z-U)-\lambda -1.}

Dies ist fast die definierende Gleichung für die Kummer-Funktionen, siehe deren Definition im Abschnitt über Streuung.

${\displaystyle K(A,B;z)\;}$ löst die Gleichung ${\displaystyle \;zK''+(B-z)K'-AK=0}$.

Ist ${\displaystyle (-A)}$ eine ganze Zahl n=0,1,2,3... dann ist K ein modifiziertes Laguerre- Polynom.

Um solche Lösungen anzupeilen, wird gesetzt: ${\displaystyle \eta =0}$ und ${\displaystyle \nu =n=0,1,2,3...}$

• Für ${\displaystyle \lambda }$ folgt: ${\displaystyle \lambda ={\sqrt {(l+{\tfrac {1}{2}})^{2}+C}}-{\tfrac {1}{2}}}$.

Mit der positiven Wurzel wie hier ist ${\displaystyle u(s)}$ bei Null regulär und normierbar wegen des abfallenden Exponentialanteils. ${\displaystyle R(x)=R_{n\lambda }(x)=K(-n,2\lambda +2;x)}$ sind Polynome. Aus ${\displaystyle {\sqrt {-E_{0}/F}}=(\lambda +1+n)/(Z-U)}$ folgen

• Die Energie-Eigenwerte ${\displaystyle F_{n\lambda }=-E_{0}\left({\frac {Z-U}{n+\lambda +1}}\right)^{2}}$.

Beim Wasserstoff-Atom gibt es in der Energie-Reihe die Hauptquantenzahl ${\displaystyle N=n+l+1}$; in diesem Modell mit Abschirmung ist die effektive Zahl im Nenner ${\displaystyle N'=n+\lambda +1}$ nicht mehr ganz und im Vergleich größer. Nimmt man die Zahl N als Referenz, dann wird die Entartung der Drehimpulse l aufgehoben, die höheren Drehimpuls-Zahlen senken die Energie ab.

Das Natrium-Atom hat den Grundzustand 3s und bekannte angeregte Orbitale 3p 4s 3d 4p 4f. Diese werden versuchsweise mit dem Schema des Modells und passenden Parametern ${\displaystyle l,n,\lambda ,Z-U,C}$ konfrontiert. (Die Spin-Orbit-Aufspaltung in ${\displaystyle 3p_{1/2}}$ und ${\displaystyle 3p_{3/2}}$, die für die doppelte D-Linie im Spektrum verantwortlich ist, wird hier unter den Teppich gekehrt.)

In der ersten Zeile wurde wohl C erraten und (Z-U) gefittet, in den folgenden eher umgekehrt. Mit konstanten Werten U,C scheint es unmöglich, die Liste zu reproduzieren. Ein Zweiparameter-Modell ist doch etwas primitiv. Es nutzt der Didaktik wegen des lösbaren Spektrums.

Hoch zum Seitenanfang