Geometrie

Belastung und Geometrie sind gleich.

Hilfsgröße ε

${\displaystyle \epsilon ={\sqrt {\frac {240}{f_{yk}}}}={\sqrt {\frac {240}{360}}}}$

ε = 0,8165

Grenz c/t

${\displaystyle {\frac {b}{t}}<37{,}8\cdot \epsilon {\frac {b}{t}}={\frac {0{,}29-6\cdot 0{,}003}{0{,}003}}}$ (DIN 18800-1 Tabelle 12)

${\displaystyle 90{,}666\not <37{,}8\cdot \epsilon }$

Beulnachweis erforderlich

k_σ= 4 (DIN 18800-1 Tabelle 12)

${\displaystyle {\overline {\lambda }}_{p}={\frac {b}{t\cdot 28{,}12176\cdot \epsilon \cdot {\sqrt {k_{\sigma }}}}}}$ (hergeleitete Gleichung 1)

${\displaystyle {\overline {\lambda }}_{p}={\frac {0{,}29-6\cdot 0{,}003}{0{,}003\cdot 28{,}12176\cdot 0{,}816\cdot {\sqrt {4}}}}}$

${\displaystyle {\overline {\lambda }}_{p}=1{,}974}$

${\displaystyle \kappa ={\frac {{\overline {\lambda }}_{p}-022}{{\overline {\lambda }}_{p}^{2}}}={\frac {1{,}974-0{,}22}{1{,}974^{2}}}}$

κ = 0,45006

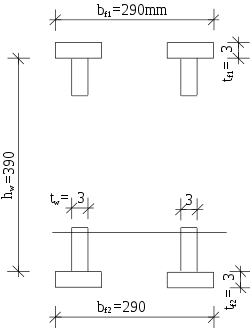
Einschub Querschnittswerte:

A_s= 4080mm²

h_s = h_w/2= 195mm

I_y= 9,685∙10^-5m⁴

I_z= 5,839∙10^-5m⁴

wirksame Flanschbreite

b_f:= κ∙(b_f -6∙t_w)+6∙t_w

b_f:= 0,45006∙(0,29-6∙0,003)+6∙0,003

b_f:= 0,1404

Vereinfachend wird mit der kürzeren Länge beider Flansche weiter gerechnet.

Bruttoquerschnittswerte

Die Formeln zur Berechnung der Querschnittswerte sind mit der Berechnung nach dem Eurocode gleich.

A_s= 3182,5mm²

h_s =195mm

I= 6,219∙10^-5m⁴

σ₂= -193,6N/mm²

σ₁= - 78,4N/mm²

Berechnung von κ_px

b= 0,39m

Randspannungsverhältnis ψ

${\displaystyle \Psi ={\frac {\sigma _{sl}}{\sigma _{1}}}={\frac {-78{,}4}{-193{,}6}}}$

ψ= 0,405

Beulwert k_σ

${\displaystyle k_{\sigma }={\frac {8{,}2}{1{,}05+\Psi }}={\frac {8{,}2}{1{,}05+0{,}405}}}$

k_σ= 5,635

Beulschlankheitsgrad ${\displaystyle {\overline {\lambda }}_{p}}$

${\displaystyle {\overline {\lambda }}_{p}={\frac {b}{t_{w}\cdot 28{,}12176\cdot \epsilon \cdot {\sqrt {k_{\sigma }}}}}}$ (Hergeleitete Gleichung)

${\displaystyle {\overline {\lambda }}_{p}={\frac {0{,}39}{0{,}003\cdot 28{,}12176\cdot 0{,}816\cdot {\sqrt {5{,}635}}}}}$

${\displaystyle {\overline {\lambda }}_{p}=2{,}385}$

Abminderungsfaktor ρ

${\displaystyle \kappa _{P}={\frac {(0{,}97+0{,}03\cdot \Psi )-(0{,}16+0{,}06\cdot \Psi )/{\overline {\lambda }}}{\overline {\lambda }}}}$ (DIN 18800-2 GL 81 Tabelle 27)

${\displaystyle \kappa _{P}={\frac {(0{,}97+0{,}03\cdot 0{,}405)-(0{,}16+0{,}06\cdot 0{,}405)/2{,}385}{2{,}385}}}$

κ_P= 0,3794

Bruttobreiten

k₁= - 0,04∙ψ² + 0,12∙ψ + 0,42 (oben) (DIN 18800-2 Tabelle 27)

k₁= - 0,04∙0,405² + 0,12∙0,405 + 0,42

k₁= 0,462

k₂= + 0,04∙ψ² - 0,12∙ψ + 0,58 (unten)

k₂= + 0,04∙0,405² - 0,12∙0,405 + 0,58

k₂= 0,538

b₁₂= b∙k₁₂

b_o= 0,39∙k₁= 0,39∙0,462

b_o= 0,1802

b_u= 0,39∙k₂= 0,39∙0,538

b_u= 0,2098

wirksame Breiten

b_u1,eff= b_u∙ρ = 0,1802∙0,3794

b_u1,eff= 0,0684

b_o1,eff= b_o∙ρ = 0,2098∙0,3794

b_o1,eff = 0,0796

Σb_eff = 0,0684 + 0,0796

Σb_eff = 0,1479

Verlust= b - Σb_eff

Verlust= 0,39 - 0,1479

Verlust= 0,2421m

Knickstabähnliches Verhalten ist ausgeschlossen, weil das Beulfeld wesentlich länger ist als es hoch ist.

Abminderungsfaktor κ_px für Plattenbeulen

κ_px= 0,3794

Wirksame Querschnittswerte

Die Berechnung der wirksamen Querschnittswerte wird übersprungen.

A_eff= 0,0017291m²

h_eff= 0,1997

I_y,eff= 5,499∙10^-5 m⁴

${\displaystyle I_{z{,}eff}=\sum {\begin{pmatrix}I_{z}\\-2\cdot (0{,}29-b_{f})^{3}\cdot t_{f}/12\\2\cdot (-Verlust)\cdot t_{w}\cdot (0{,}29/2-1{,}5\cdot t_{w})^{2}\end{pmatrix}}}$

${\displaystyle I_{z{,}eff}=\sum {\begin{pmatrix}5{,}839\cdot 10^{-5}\\-2\cdot (0{,}29-0{,}14)^{3}\cdot 0{,}003/12\\-2\cdot 0{,}2421\cdot 0{,}003\cdot (0{,}145-1{,}5\cdot 0{,}003)^{2}\end{pmatrix}}}$

I_z,eff= 10^-5∙(5,839 - 0,1687 - 2,868)

I_z,eff= 2,805∙10^-5m⁴

Widerstandsmoment oben	Widerstandsmoment unten
${\displaystyle W_{eff{,}o}={\frac {I}{Z}}={\frac {I_{eff}}{h_{s{,}eff}+t_{f1}/2}}}$	${\displaystyle W_{eff{,}u}={\frac {I}{Z}}={\frac {I_{eff}}{h_{w}-h_{s{,}eff}+t_{f2}/2}}}$
${\displaystyle W_{eff{,}o}={\frac {5{,}499\cdot 10^{-5}}{0{,}1997+0{,}003/2}}}$	${\displaystyle W_{eff{,}u}={\frac {5{,}499\cdot 10^{-5}}{0{,}39-0{,}1997+0{,}003/2}}}$
Weff,o= 2,733∙10-4m³	Weff,u= 2,867∙10- 4m³
MRd= Weff,o∙fyd	MRd,u= Weff,u∙fyd
MRd= 2,733∙10-4∙360000/1,1	MRd,u= 2,867∙10- 4∙360000/1,1
MRd= 89,43kNm	MRd,u= 93,83kNm

Der verschobene Schwerpunkt erhöht das Moment.

M_Ed,N= M_Ed + N_Ed∙(H_s,eff - H_s)

M_Ed,N= 18,375 + ( - 433,1)∙(0,195 - 0,1997)= 18,375+ 2,039

M_Ed,N= 20,41kNm

Nachweis

${\displaystyle \eta _{1}={\frac {M_{Ed{,}N}}{f_{yd}\cdot W_{eff{,}o}}}-{\frac {N}{f_{yd}\cdot A_{eff}}}}$

${\displaystyle \eta _{1}={\frac {0{,}02041\cdot 1{,}1}{0{,}0002733\cdot 360}}+{\frac {0{,}4331\cdot 1{,}1}{360\cdot 0{,}001729}}}$

η₁= 0,2282 + 0,7654

η₁= 0,9936

Nachweis erfüllt

Querschnittsnachweis unten

${\displaystyle \eta _{1u}=-{\frac {M_{Ed{,}N}}{f_{yd}\cdot W_{eff{,}u}}}-{\frac {N}{f_{yd}\cdot A_{eff}}}}$

${\displaystyle \eta _{1u}=-{\frac {0{,}02041\cdot 1{,}1}{0{,}0002867\cdot 360}}+{\frac {0{,}4331}{360\cdot 0{,}0017291}}}$

η_1u= - 0,2176 + 0,6958

η_1u= 0,4782

Nachweis erfüllt

Biegeknicknachweis

Nachweis gegen Biegeknicken um die schwache Achse

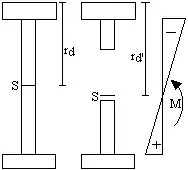
'= bezieht sich auf dem wirksamen Querschnitt

r_d und r'_d= Abstand des Biegedruckrandes vom Schwerpunkt

r_d = 0,145

r'_d= 0,145

${\displaystyle i'={\sqrt {\frac {I'}{A'}}}={\sqrt {\frac {2{,}805\cdot 10^{-5}}{0{,}0017291}}}}$ (DIN 18800-2 Gleichung 94)

i'= 0,1274m

${\displaystyle i={\sqrt {\frac {I}{A}}}={\sqrt {\frac {5{,}839\cdot 10^{-5}}{0{,}00408}}}}$

i= 0,1196m

${\displaystyle \lambda _{a}=\pi \cdot {\sqrt {\frac {E}{f_{yk}}}}=\pi \cdot {\sqrt {\frac {210000}{360}}}}$

λ_a= 75,87

${\displaystyle {\overline {\lambda }}'={\frac {s_{k}}{i'\cdot \lambda _{a}}}={\frac {7}{75{,}87\cdot 0{,}127}}}$ (DIN 18800-2 Gleichung 93)

${\displaystyle {\overline {\lambda }}'=0{,}724}$

${\displaystyle \alpha '=\alpha \cdot {\frac {i\cdot r'_{d}}{i'\cdot r_{d}}}}$ mit α=0,34 (DIN 18800-2 Gleichung 92)

${\displaystyle \alpha '=0{,}34\cdot {\frac {0{,}1196\cdot 0{,}145}{0{,}1274\cdot 0{,}145}}}$

α'= 0,319

Δ_wo= |h_s-h_eff|

Δ_wo= 0,195-0,195

Δ_wo= 0

${\displaystyle k'=0{,}5\cdot \left(1+\alpha '\cdot ({\overline {\lambda }}'_{k}-0{,}2)+{\overline {\lambda }}_{k}^{\prime 2}+\Delta _{w0}\cdot r_{d}'/i^{2}\right)}$ (DIN 18800-2 Gleichung 91)

k'= 0,5∙(1+0,319∙(0,724-0,2)+ 0,724²+ 0)

k'= 0,846

${\displaystyle \kappa '={\frac {1}{k'+{\sqrt {k^{\prime 2}-{\overline {\lambda }}_{k}^{\prime 2}}}}}}$ (DIN 18800-2 Gleichung 90)

${\displaystyle \kappa '={\frac {1}{0{,}846+{\sqrt {0{,}846^{2}-0{,}725^{2}}}}}}$

κ' = 0,7793

Nachweis

${\displaystyle \eta ={\frac {N\cdot \gamma }{\kappa '\cdot A'\cdot f_{yk}}}<1}$ (DIN 18800-2 Gleichung 89 und 3)

${\displaystyle \eta ={\frac {0{,}433\cdot 1{,}1}{0{,}7793\cdot 0{,}0017291\cdot 360}}}$

η= 0,9821

Nachweis gegen Biegeknicken um die starke Achse

r_d = h_s+t_f= 0,195+ 0,003

r_d = 0,198

r_d'= h_s,eff+ t_f= 0,1997+ 0,003

r_d'= 0,2027

${\displaystyle i'={\sqrt {\frac {I'}{A'}}}={\sqrt {\frac {5{,}499\cdot 10^{-5}}{0{,}0017291}}}}$ (DIN 18800-2 Gleichung 94)

i'= 0,1783m

${\displaystyle i={\sqrt {\frac {I}{A}}}={\sqrt {\frac {9{,}685\cdot 10^{-5}}{0{,}00408}}}}$

i= 0,1541m

${\displaystyle \lambda _{a}=\pi \cdot {\sqrt {\frac {E}{f_{yk}}}}=\pi \cdot {\sqrt {\frac {210000}{360}}}}$

λ_a= 75,87

${\displaystyle {\overline {\lambda }}'={\frac {s_{k}}{i'\cdot \lambda _{a}}}={\frac {7}{0{,}1783\cdot 75{,}87}}}$ (DIN 18800-2 Gleichung 93)

${\displaystyle {\overline {\lambda }}'=0{,}517}$

${\displaystyle \alpha '=\alpha \cdot {\frac {i\cdot r'_{d}}{i'\cdot r_{d}}}}$mit α=0,34 (DIN 18800-2 Gleichung 92)

${\displaystyle \alpha '=0{,}34\cdot {\frac {0{,}1541\cdot 0{,}2027}{0{,}1783\cdot 0{,}198}}}$

α'= 0,3007

Δ_wo= |h_s-h_eff| = 0,1997-0,195

Δ_wo= 0,00471

${\displaystyle k'=0{,}5\cdot \left(1+\alpha '\cdot ({\overline {\lambda }}'_{k}-0{,}2)+{\overline {\lambda }}_{k}^{\prime 2}+\Delta _{w0}\cdot r_{d}'/i^{2}\right)}$ (DIN 18800-2 Gleichung 91)

k'= 0,5∙(1+0,3∙(0,517-0,2)+ 0,517²+ 0,00471∙0,2027/0,1541²)

k'= 0,702

${\displaystyle \kappa '={\frac {1}{k'+{\sqrt {k^{\prime 2}-{\overline {\lambda }}_{k}^{\prime 2}}}}}}$ (DIN 18800-2 Gleichung 90)

${\displaystyle \kappa '={\frac {1}{0{,}702+{\sqrt {0{,}702^{2}-0{,}517^{2}}}}}}$

κ' = 0,8506

Nachweis für die Normalkraft

${\displaystyle \eta ={\frac {N\cdot \gamma }{\kappa '\cdot A'\cdot f_{yk}}}<1}$ (DIN 18800-2 Gleichung 89 und 3)

${\displaystyle \eta ={\frac {0{,}4331\cdot 1{,}1}{0{,}8506\cdot 0{,}0017291\cdot 360}}}$

η= 0,8998

Nach DIN 18800-2 Element 719 sind in dem Biegeknicknachweis folgende Größen aus zu wechseln:

N_pl,d → N'_Pl,d

M_pl,d → M'_pl,d

κ → κ'

${\displaystyle {\overline {\lambda }}_{k}\to {\overline {\lambda }}'_{k}}$

N_Pl,d= A'∙f_yd (DIN 18800-2 Gleichung 96)

M_Pl,d= I'∙f_yd/r_d' (DIN 18800-2 Gleichung 97)

Berechnung des plastischen Momentes
Bei doppelsymmetrischen Querschnitten, die durch ein positives Moment verbeult werden, liegt die Flächenhalbierende immer unter dem Loch. Für Stegteile, die an der Flächenhalbierenden angrenzen, ist Abstand zur Flächenhalbierenden halb so groß wie die Länge des Stegteils. Die Ergebnisse werden in einer Tabelle zusammengefasst:

wirksame Querschnittsteile

${\displaystyle W_{Pl}=\sum {\begin{pmatrix}0{,}003\cdot 0{,}318\cdot 0{,}14\\0{,}0684\cdot 0{,}282\cdot 0{,}006\\0{,}0056\cdot 0{,}0028\cdot 0{,}006\\0{,}074\cdot 0{,}037\cdot 0{,}006\\0{,}003\cdot 0{,}0755\cdot 0{,}14\end{pmatrix}}=\sum {\begin{pmatrix}1{,}34\cdot 10^{-4}\\1{,}16\cdot 10^{-4}\\9{,}46\cdot 10^{-8}\\1{,}64\cdot 10^{-5}\\3{,}18\cdot 10^{-5}\end{pmatrix}}}$

W_Pl= 2,977∙10^-4m³

M_Pl= W_Pl∙f_yd= 2,977∙10^-4∙360/1,1

M_Pl= 0,097MN

M_Pl= 97,42kN

Nachweis

${\displaystyle \Delta _{n}=\eta \cdot (1-\eta )\cdot \kappa ^{2}\cdot {\overline {\lambda }}_{k}^{2}}$

Δ_n = 0,8998∙(1-0,8998) ∙0,8506²∙0,517²

Δ_n = 0,01746

${\displaystyle {\frac {N}{\kappa \cdot N_{Pl}}}+{\frac {\beta _{m}\cdot M}{M_{Pl{,}d}}}+\Delta _{n}<1}$ (DIN 18800-2 Gleichung 24)

${\displaystyle {\frac {0{,}4331\cdot 1{,}1}{0{,}8506\cdot 0{,}0017291\cdot 360}}+{\frac {1\cdot 21{,}8282}{97{,}42}}+0{,}01746}$

0,8998+ 0,2096+ 0,01746

${\displaystyle 1{,}127\not <1}$

Nachweis nicht erfüllt

Schubbeulen und Interaktion

Für Schubbeulen wird der schnelle Nachweis verwendet

V= 10,5kN

k_τ= 5,34 für lange Felder

${\displaystyle {\frac {\gamma \cdot V_{Ed}}{17{,}949\cdot f_{yk}\cdot t^{2}\cdot \epsilon \cdot {\sqrt {k_{\tau }}}}}<1}$ (Hergeleitete Formel 5)

${\displaystyle {\frac {1{,}1\cdot 0{,}0105}{17{,}949\cdot 360\cdot (2\cdot 0{,}003^{2})\cdot 0{,}8165\cdot {\sqrt {5{,}34}}}}}$

0,0526 < 1

Neben dem Beulnachweis ist noch der reguläre Querkraftnachweis zu führen.

${\displaystyle {\frac {V\cdot {\sqrt {3}}}{A\cdot f_{yd}}}={\frac {0{,}0105\cdot {\sqrt {3}}\cdot 1{,}1}{2\cdot 0{,}003\cdot 0{,}39\cdot 360}}}$

0,0237 < 1

Nachweis erfüllt

Die Interaktion mindert die Stegdicken ein weiteres Mal ab. Da aber Schub und Biegung an verschiedenen Stellen auftreten, muss die Interaktion nicht geführt werden.

Modell der wirksamen Spannungen nach der DIN 18800-3

Für den Knicknachweis werden die beiden Abminderungsfaktoren für Knicken und Beulen multipliziert. Bei der DIN wird nicht wie im Eurocode gefordert, dass mit wirksamen Breiten gerechnet wird. Der Knicknachweis wird daher mit Bruttobreiten geführt. Es werden folgende Werte übernommen:

σ₂= -193,6N/mm²

κ_px= 0,3794

i_z= 0,1196

i_y= 0,1541

Knicken um die schwache Achse	Knicken um die starke Achse
λa= 75,87	λa= 75,87
${\displaystyle {\overline {\lambda }}={\frac {s_{k}}{i\cdot \lambda _{a}}}={\frac {7}{75{,}87\cdot 0{,}1196}}}$	${\displaystyle {\overline {\lambda }}={\frac {s_{k}}{i\cdot \lambda _{a}}}={\frac {7}{75{,}87\cdot 0{,}1541}}}$
${\displaystyle {\overline {\lambda }}=0{,}771}$	${\displaystyle {\overline {\lambda }}=0{,}599}$
${\displaystyle k=0{,}5\cdot (1+\alpha \cdot ({\overline {\lambda }}_{k}-0{,}2)+{\overline {\lambda }}_{k}^{2})}$	${\displaystyle k=0{,}5\cdot (1+\alpha \cdot ({\overline {\lambda }}_{k}-0{,}2)+{\overline {\lambda }}_{k}^{2})}$
k= 0,5∙(1+ 0,34∙(0,771-0,2)+ 0,771²)	k= 0,5∙(1+ 0,34∙(0,599-0,2)+ 0,599²)
k= 0,894	k= 0,747
${\displaystyle \kappa ={\frac {1}{k+{\sqrt {k^{2}-{\overline {\lambda }}_{k}^{2}}}}}}$	${\displaystyle \kappa ={\frac {1}{k+{\sqrt {k^{2}-{\overline {\lambda }}_{k}^{2}}}}}}$
${\displaystyle \kappa ={\frac {1}{0{,}894+{\sqrt {0{,}894^{2}-0{,}771^{2}}}}}}$	${\displaystyle \kappa ={\frac {1}{0{,}747+{\sqrt {0{,}747^{2}-0{,}599^{2}}}}}}$
κ = 0,74206	κ = 0,83766

Von den beiden Abminderungsfaktoren ist der kleinste maßgebend.

aufnehmbare Spannung σ_P,Rd

σ_P,Rd= κ∙κ_px∙f_yd

σ_P,Rd= 0,74206∙0,3794∙360/1,1

σ_P,Rd= 92,13N/mm²

Nachweis

${\displaystyle {\frac {\sigma _{Ed}}{\sigma _{P{,}Rd}}}={\frac {193{,}6}{92{,}13}}}$

${\displaystyle 2{,}102\not <1}$

Nachweis nicht erfüllt

Wo befindet sich ${\displaystyle {\frac {N}{\kappa \cdot N_{Pl}}}+{\frac {\beta _{m}\cdot M}{M_{Pl{,}d}}}+\Delta _{n}}$? Dieser Nachweis muss nicht geführt werden, weil die Spannung aus dem Moment schon im Beulfeld enthalten ist. σ_Ed ist die größte Randspannung.

Allgemein:Inhaltsverzeichnis ; Glossar ; Zahlen

Rechenbeispiel: Allgemeiner Lösungsweg ; erstes ; zweites ; drittes ; viertes

Norm: Eurocode ;DIN ;Zusammenfassung