Geometrie

Es wird die gleiche Geometrie verwendet.
Für den Druckflansch muss ein b/t-Nachweis geführt werden.
Grenz b/t

${\displaystyle {\frac {b}{t}}<12{,}9{\frac {b}{t}}={\frac {91-3}{2\cdot 7}}}$

6,286 < 12,9

Grenz b/t eingehalten

Bruttoquerschnittswerte

Fläche A= 0,00265m²

Schwerpunkt h_s= 0,251m

Spannungsnulllinie S= 0,4m

Flächenmoment zweiten Grades I= 0,0001258m⁴

Spannung oben σ₂= 127,6 N/mm²

Spannung neben der oberen Steife σ_sl2= - 63,8 N/mm²

Spannung neben der unteren Steife σ_sl1= - 159,5 N/mm²

Spannung unten σ₁= - 255,2 N/mm²

Berechnung von κ_px

Die Berechnung der wirksamen Breiten durch die Einzelfelder wird ähnlich geführt wie im Eurocode. Dabei ist ${\displaystyle \rho ={\frac {{\overline {\lambda }}_{p}-0{,}055\cdot (3+\Psi )}{{\overline {\lambda }}_{p}^{2}}}}$ durch ${\displaystyle \rho ={\frac {(0{,}97+0{,}03\cdot \Psi )-(0{,}16+0{,}06\cdot \Psi )/{\overline {\lambda }}}{\overline {\lambda }}}}$zu ersetzen. Wirksame Breiten werden nicht benötigt, sondern nur die Abminderungsfaktoren. Diese werden in einer Tabelle zusammengefasst.

Die DIN hat keine Formeln zur Berechnung des Beulwertes und verweist auf die Literatur. Um den Beulwert des Gesamtfeldes zu berechnen, werden zuerst die wirksamen Breiten ausgerechnet und dann nach dem Eurocode verfahren. Dabei werden zuerst die Querschnittswerte der ersten Steife, der zweiten Steife und der zusammengeführten Steife berechnet. Dann wird die ideale Beulspannung aus den 3 Steifen errechnet und die kleinste ist maßgebend. Aus dieser wird dann der Beulwert rückgerechnet. Der Rechenweg wird übersprungen.

Alternative Literatur ist das Buch „Beulwerte ausgesteifer Rechteckplatten“ von Klöppel und Scheer. Aus diesem kann schnell ein genauerer und größerer Beulwert entnommen werden. Dazu werden die Steifenkennwerte benötigt. In I sind wirksame Breiten enthalten.

Steifenkennwerte

I= 7,025∙10^-8m⁴

${\displaystyle \gamma ={\frac {12\cdot (1-\nu ^{2})\cdot I}{h_{w}\cdot t_{w^{3}}}}}$ (DIN 18800-3 Element 114)

${\displaystyle \gamma ={\frac {10{,}92\cdot 7{,}025\cdot 10^{-8}}{0{,}6\cdot 0{,}003^{3}}}}$

γ = 47,35

${\displaystyle \delta ={\frac {A_{s}}{t_{w}\cdot h_{w}}}={\frac {180}{3\cdot 600}}}$ mit A_s= 180mm² (DIN 18800-3 Element 114)

δ = 0,1

ψ= - 0,5

${\displaystyle \alpha ={\frac {5}{0{,}6}}=8{,}33}$

„Zufällig“ gibt es dafür ein Diagramm in dem Buch.

Beulwert ablesen

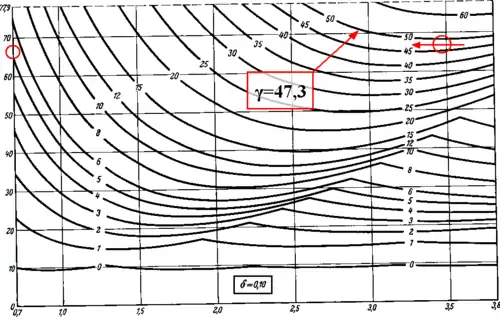
Auf der X-Achse ist α aufgetragen. Dieser Wert geht jedoch nur bis 3,8 und nicht bis 8,33. Auf der y-Achse ist der Beulwert. Im Diagramm sind mehrere Kurven für unterschiedliche γ. Da α=8,33 im Diagramm nicht enthalten ist, wird der Mindestwert der Kurve für γ = 47,35 verwendet. Ein Beulwert von k_σ= 67 kann abgelesen werden. Der Eurocode schlägt für a_c= 2,08 vor. a_c ist diejenige Länge, die zwischen den beiden Formeln des Eurocodes unterscheidet. Dividiert man a_c durch die Steghöhe, so ergibt sich 3,4. Dies ist genau der Minimumwert im Diagramm. Ändert man die Geometrie und Belastung, so findet der Eurocode den Ort des Minimums. Ganz anders sieht es mit dem Beulwert aus. Der Eurocode liefert nur k_σ= 26,2.

Die ideale Beulspannung kann sofort berechnet werden.

k_σ= 67

${\displaystyle \sigma _{e}=190000\cdot \left({\frac {t}{b}}\right)^{2}=190000\cdot \left({\frac {0{,}003}{0{,}6}}\right)^{2}}$ (DIN 18800-3 Element 113)

σ_e= 4,75N/mm²

σ_pi= k_σ∙ σ_e= 67∙ 4,75 (DIN 18800-3 Element 113)

σ_pi= 318,25∙N/mm²

plattenartiges Verhalten

${\displaystyle {\overline {\lambda }}_{p}={\sqrt {\frac {f_{yk}}{\sigma _{pi}}}}={\sqrt {\frac {360}{318}}}}$

${\displaystyle {\overline {\lambda }}_{p}=1{,}063}$

${\displaystyle \kappa _{p}=MIN(1{,}25;1{,}25-0{,}25\cdot \Psi )\cdot \left({\frac {1}{\overline {\lambda }}}-{\frac {0{,}22}{{\overline {\lambda }}^{2}}}\right)}$ (DIN 18800-3 Tabelle 1)

${\displaystyle \kappa _{p}=1{,}25\cdot \left({\frac {1}{1{,}063}}-{\frac {0{,}22}{1{,}063^{2}}}\right)}$

κ_p= 0,93218

knickstabähnliches Verhalten

${\displaystyle k=0{,}5\cdot \left(1+0{,}34\cdot \left({\overline {\lambda }}_{p}-0{,}2\right)+{\overline {\lambda }}_{p^{2}}\right)}$

k= 0,5∙(1 + 0,34∙(1,063 - 0,2) + 1,063²)

k= 1,212

${\displaystyle \kappa _{k}={\frac {1}{k+{\sqrt {k^{2}-{\overline {\lambda }}_{p^{2}}}}}}}$

${\displaystyle \kappa _{k}={\frac {1}{1{,}212+{\sqrt {1{,}212^{2}-1{,}063^{2}}}}}}$

κ_k= 0,55729

Interaktion

${\displaystyle {\frac {\sigma _{pi}}{\sigma _{ki}}}=k_{\sigma }\cdot \alpha ^{2}\cdot {\frac {1+\Sigma \delta _{L}}{1+\Sigma \gamma _{L}}}}$ (DIN 18800-3 Gleichung 23)

${\displaystyle {\frac {\sigma _{pi}}{\sigma _{ki}}}=67\cdot \left({\frac {5}{0{,}6}}\right)^{2}\cdot {\frac {1+0{,}1}{1+47{,}4}}}$

${\displaystyle {\frac {\sigma _{pi}}{\sigma _{ki}}}=105{,}9}$

${\displaystyle \Lambda ={\overline {\lambda }}_{p}^{2}+0{,}5}$ und Λ wird zwischen 2< Λ <4 begrenzt (DIN 18800-3 Gleichung 22)

Λ= 1,063² + 0,5

Λ= 2

${\displaystyle \rho ={\frac {\Lambda -\sigma _{pi}/\sigma _{ki}}{\Lambda -1}}}$und ρ wird zwischen 0 < ρ < 1 begrenzt Gleichung 21

${\displaystyle \rho ={\frac {2-105{,}7}{2-1}}}$

ρ= 0

κ_px= (1 - ρ²)∙κ_p + ρ²∙κ_k (DIN 18800-3 Gleichung 24)

κ_px= (1 - 0²)∙0,93218 + 1²∙0,55729

κ_px= 0,93218

Nachweis

σ_d= 255,2N/mm²

σ_p,Rd= f_yd∙MIN(κ₁;κ₂;κ₃;κ_px) (DIN 18800-3 Gleichung 11)

mit κ₁ und κ₂ als Abminderungsfaktoren für Einzelfeldbeulen

σ_p,Rd= 360/1,1∙MIN(0,8088;0,8701;1;0,93218)= 360∙0,8088/1,1

σ_p,Rd= 264,7

${\displaystyle {\frac {\sigma _{d}}{\sigma _{p{,}Rd}}}={\frac {255{,}2}{264{,}7}}<1}$ (DIN 18800-3 Gleichung 9)

0,9643 < 1

Nachweis erfüllt.

Schubbeulen

Da die DIN keine Formel für einen Schubbeulwert mit Längssteifen enthält, wird die Formel aus dem Eurocode verwendet. Da auch der Rechenweg bis ${\displaystyle {\overline {\lambda }}_{p}}$gleich ist, werden die Werte bis dahin übernommen.

k_τ= 9,518

${\displaystyle {\overline {\lambda }}_{p}={\frac {h_{w}}{37{,}01\cdot t\cdot \epsilon \cdot {\sqrt {k_{\tau }}}}}}$ (Hergeleitete Formel)

${\displaystyle {\overline {\lambda }}_{p}={\frac {0{,}6}{37{,}01\cdot 0{,}003\cdot 0{,}813\cdot {\sqrt {9{,}52}}}}}$

${\displaystyle {\overline {\lambda }}_{p}=2{,}144}$

Die Berechnung der Schubschlankheit für das Einzelfeld ist mit dem Eurocode ähnlich. Der Wert wird übernommen.

${\displaystyle {\overline {\lambda }}_{p}=1{,}4144}$

Einzelfeldbeulen ist maßgebend.

${\displaystyle {\overline {\lambda }}_{p}=MIN(2{,}144;1{,}4144)=2{,}144}$

Für ${\displaystyle {\overline {\lambda }}_{p}>1{,}38}$ und Beulfeld mit Längssteifen gilt

${\displaystyle \kappa _{\tau }={\frac {1{,}16}{{\overline {\lambda }}_{p}^{2}}}={\frac {1{,}16}{2{,}144^{2}}}}$ (DIN 18800-3 Tabelle 1)

κ_τ = 0,25232

Nachweis

${\displaystyle \tau _{d}={\frac {V}{A}}={\frac {70{,}13}{0{,}6\cdot 0{,}003}}}$

τ_d= 38,96N/mm²

${\displaystyle \tau _{P{,}Rd}={\frac {f_{yk}\cdot \kappa _{\tau }}{{\sqrt {3}}\cdot \gamma }}}$ (DIN 18800-3 Gleichung 12)

${\displaystyle \tau _{P{,}Rd}={\frac {360\cdot 0{,}25232}{{\sqrt {3}}\cdot 1{,}1}}}$

τ_P,Rd= 47,67N/mm²

${\displaystyle {\frac {\tau _{d}}{\tau _{P{,}Rd}}}={\frac {38{,}96}{47{,}67}}}$ (DIN 18800-3 Gleichung 10)

0,8173 < 1 Nachweis erfüllt

Lokales Beulen aus einer Einzellast

F= 9,3kN

s_s= 0,05m

c= s_s + 2∙t_f2= 0,05 + 2∙0,003

c= 0,056

${\displaystyle \alpha ={\frac {a}{b}}={\frac {5}{0{,}6}}}$

α= 8,33

${\displaystyle \beta ={\frac {c}{a}}={\frac {0{,}056}{5}}}$

ß= 0,0112

Aus der Tabelle kann entnommen werden:

${\displaystyle z=z_{lo}+(z_{ro}-z_{lo})\cdot {\frac {x-x_{1}}{x_{2}-x_{1}}}+\left(z_{lu}-z_{lo}+(z_{ru}-z_{lu}+z_{lo}-z_{ro})\cdot \left({\frac {x-x_{1}}{x_{2}-x_{1}}}\right)\right)\cdot \left({\frac {y-y_{1}}{y_{2}-y_{1}}}\right)}$

${\displaystyle k_{\sigma y}=0{,}25+(0{,}2-0{,}25)\cdot {\frac {8{,}{\overline {3}}-8}{10-8}}+\left(0{,}4-0{,}25+(0{,}35-0{,}4+0{,}25-0{,}2)\cdot \left({\frac {8{,}{\overline {3}}-8}{10-8}}\right)\right)\cdot \left({\frac {0{,}0112-0}{0{,}1-0}}\right)}$

k_σy= 0,25 - 0,00833 + (0,15 + 0∙0,166)∙0,112

k_σy= 0,2584666

σ_e= 4,75N/mm²

σ_y,pi= k_σy∙σ_e∙a/c

σ_y,pi= 0,2584666∙4,75∙5/0,056

σ_y,pi= 109,61N/mm²

${\displaystyle {\overline {\lambda }}_{py}={\sqrt {\frac {f_{yk}}{\sigma _{y{,}pi}}}}={\sqrt {\frac {360}{109{,}61}}}}$

${\displaystyle {\overline {\lambda }}_{py}=1{,}8122}$

${\displaystyle \kappa _{y}=\left({\frac {1}{\overline {\lambda }}}-{\frac {0{,}22}{{\overline {\lambda }}^{2}}}\right)=\left({\frac {1}{1{,}8122}}-{\frac {0{,}22}{1{,}8122^{2}}}\right)}$ (DIN 18800-3 Tabelle 1)

κ_y= 0,48482

σ_yki= 1,88•σ_e= 8,93N/mm²

Es wird laut DIN die Beulschlankheit :${\displaystyle {\overline {\lambda }}_{py}^{2}}$ verwendet.

${\displaystyle k=0{,}5\cdot \left(1+0{,}34\cdot \left({\overline {\lambda }}_{py}-0{,}2\right)+{\overline {\lambda }}_{py}^{2}\right)}$

k= 0,5∙(1 + 0,34∙(1,8122 - 0,2) + 1,8122²)

k= 2,416

${\displaystyle \kappa _{k}={\frac {1}{k+{\sqrt {k^{2}-{\overline {\lambda }}_{p}^{2}}}}}}$

${\displaystyle \kappa _{k}={\frac {1}{2{,}416+{\sqrt {2{,}416^{2}-1{,}8122^{2}}}}}}$

κ_k= 0,24912

${\displaystyle {\frac {\sigma _{y{,}pi}}{\sigma _{yki}}}={\frac {109{,}61}{8{,}93}}=12{,}27}$

${\displaystyle \Lambda ={\overline {\lambda }}_{p}^{2}+0{,}5}$ und 2< Λ <4 (DIN 18800-3 Gleichung 22)

Λ= 1,8122² + 0,5

Λ= 3,78

${\displaystyle \rho ={\frac {\Lambda -\sigma _{pi}/\sigma _{ki}}{\Lambda -1}}}$ und 0 < ρ < 1(DIN 18800-3 Gleichung 21)

${\displaystyle \rho ={\frac {3{,}78-12{,}27}{3{,}78-1}}}$

ρ= 0

κ_px= (1 - ρ²)∙κ_p + ρ²∙κ_k(DIN 18800-3 Gleichung 24)

κ_px= (1 - 0²)∙0,48482 + 1²∙0,24912

κ_px= 0,48482

σ_P,Rd= f_yd∙ κ_px = 360∙0,485/1,1

σ_P,Rd= 158,7

σ_y= F/(c∙t_w)

σ_y= 9,3/(0,056∙0,003)

σ_y= 55,36N/mm²

Nachweis

${\displaystyle {\frac {\sigma _{y}}{\sigma _{P{,}Rd}}}={\frac {55{,}36}{158{,}7}}}$

${\displaystyle {\frac {\sigma _{y}}{\sigma _{P{,}Rd}}}=0{,}3489}$

Nachweis erfüllt

Interaktion

:κx= 0,93218	Nachweis η1: 0,9643
:κy= 0,48482	Nachweis η2: 0,3489
:κτ= 0,25232	Nachweis η3: 0,8173

e₁= 1 + κ_x4= 1 + 0,93218⁴(DIN 18800-3 Gleichung 15)

e₁= 1,754

e₂= 1 + κ_y4= 1 + 0,48482⁴(DIN 18800-3 Gleichung 16)

e₂= 1,055

e₃= 1 + κ_x∙ κ_y∙ κ_τ² = 1 + 0,93218∙0,48482∙0,25232²(DIN 18800-3 Gleichung 17)

e₃= 1,029

V= (κ_x∙ κ_y)⁶= (0,93218∙0,48482)⁶(DIN 18800-3 Gleichung 18)

V= 0,00852

${\displaystyle \left({\frac {|\sigma _{x}|}{\sigma _{xP{,}R{,}d}}}\right)^{e_{1}}+\left({\frac {|\sigma _{y}|}{\sigma _{yP{,}R{,}d}}}\right)^{e_{1}}+\left({\frac {\tau }{\tau _{P{,}R{,}d}}}\right)^{e_{3}}-V\cdot \left({\frac {|\sigma _{x}\cdot \sigma _{y}|}{\sigma _{xP{,}R{,}d}\cdot \sigma _{xP{,}R{,}d}}}\right)<1}$ (DIN 18800-3 Gleichung 14)

0,9643^1,754 + 0,3489^1,055 + 0,8173^1,029 - 0,00852∙0,9643∙0,3489

2,077 > 1

Nachweis nicht erfüllt

Benutzt man die Gleichung aus dem Eurocode, so würde man auf ein günstigeres Ergebnis kommen:

${\displaystyle {\sqrt {\left({\frac {\sigma _{x{,}Ed}\cdot \gamma _{M1}}{\rho _{x}\cdot f_{y}}}\right)^{2}+\left({\frac {\sigma _{z{,}Ed}\cdot \gamma _{M1}}{\rho _{z}\cdot f_{y}}}\right)^{2}-\left({\frac {\sigma _{x{,}Ed}\cdot \gamma _{M1}}{\rho _{x}\cdot f_{y}}}\right)\cdot \left({\frac {\sigma _{z{,}Ed}\cdot \gamma _{M1}}{\rho _{z}\cdot f_{y}}}\right)+3\cdot \left({\frac {\tau _{Ed}\cdot \gamma _{M1}}{\chi _{w}\cdot f_{y}}}\right)^{2}}}}$< 1

${\displaystyle {\sqrt {0{,}9643^{2}+0{,}3489^{2}-0{,}9643\cdot 0{,}3489+3\cdot 0{,}8173}}=1{,}78}$

Sonstige Nachweise

Mindestanforderungen an die Längssteife
Die Mindestanforderung gegen Biegedrillknicken nach Gleichung 34 und 35 ist mit dem Eurocode identisch. Nachweis

${\displaystyle {\frac {5{,}3\cdot f_{y}\cdot I_{p}}{I_{T}\cdot E}}<1}$(DIN 18800-3 Gleichung 34)

${\displaystyle 1{,}044\not <1}$

Nachweis fast erfüllt

Endquersteife
Für Endquersteifen muss ein Nachweis geführt werden, wenn

V > V_pi = h_w∙t_w∙τ_pi (DIN 18800-3 Gleichung 27)

V_Pi= 600∙3∙45,2= 81360N

V_Pi= 81,36kN > V= 70,13

Nachweis nicht erforderlich

Allgemein:Inhaltsverzeichnis ; Glossar ; Zahlen

Rechenbeispiel: Allgemeiner Lösungsweg ; erstes ; zweites ; drittes ; viertes

Norm: EuroB ;DINS ;EuroS ;DINB ;Zusammenfassung ;Variation der Geometrie