Physik Oberstufe/ Elektrizitätslehre/ Induktion

Der im Magnetfeld bewegte Leiter

Lorentzkraft und Induktion

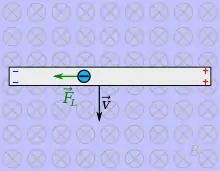
Experiment: Leiterschaukel: Auf einen stromdurchflossenen Leiter wirkt im Magnetfeld eine Kraft. Ursache ist die Lorentzkraft auf bewegte Ladungen, hier die Elektronen im Leiter.

Umkehrung: Die Leiterschleife wird bewegt.
Beobachtung: Das Voltmeter zeigt eine Spannung, genannt Induktionsspannung, an.
Erklärung: Ursache ist wieder die Lorentzkraft, die die Elektronen im Leiter senkrecht zur Bewegungsrichtung verschiebt.

Leite ein Formel zur Berechnung der Induktionsspannung $U_{\rm {ind}}$ ab. Es gilt:

F_{\rm {L}}=e\cdot v\cdot B

F_{\rm {el}}=e\cdot E=e\cdot {\frac {U_{\rm {ind}}}{d}}

Die Elektronen werden so lange verschoben, bis diese beiden Kräfte im Gleichgewicht sind. Dann gilt:

F_{\rm {L}}=F_{\rm {el}}

e\cdot v\cdot B=e\cdot E=e\cdot {\frac {U_{\rm {ind}}}{d}}\qquad \Leftrightarrow

$U_{\rm {ind}}=d\cdot v\cdot B\,.$

Energieerhaltung

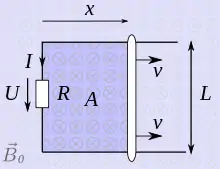
Induktionsstrom durch einen im Feld bewegten Leiter.

Fließt ein Strom, so wirkt die Lorentzkraft entgegen der Bewegungsrichtung.

Experiment: Aufbau wie zuvor, aber statt Voltmeter wird ein Widerstand $R$ angeschlossen. Dadurch fließt ein Strom $I$ . Auf den Leiter wirkt nun eine Kraft ${\vec {F}}_{\rm {m}}$ die entgegen der Geschwindigkeit ${\vec {v}}$ wirkt.

Zeige, dass der Energieerhaltungssatz gilt.

Für die elektrische Leistung $P$ gilt:

P_{\rm {el}}=U_{\rm {ind}}\cdot I\,,

für die mechanische Leistung:

P_{\rm {mech}}={\frac {\Delta W}{\Delta t}}={\frac {F_{\rm {m}}\cdot \Delta x}{\Delta t}}=F_{\rm {m}}\cdot {\frac {\Delta x}{\Delta t}}=F_{\rm {m}}\cdot v\,.

Wenn man nun für die magnetische Kraft $F_{\rm {m}}$ auf den Leiter:

F_{\rm {m}}=d\cdot I\cdot B

einsetzt und für die Induktionspannung $U_{\rm {ind}}$ :

U_{\rm {ind}}=d\cdot v\cdot B

verwendet, so sieht man, dass

P_{\rm {el}}=P_{\rm {mech}}

ist. Die mechanisch aufgebrachte Leistung wird vollständig in elektrische Leistung umgesetzt.

Das Induktionsgesetz im allgemeinen Fall

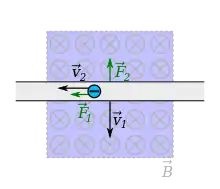
Eine Änderung des magnetischen Flusses in der linken Spule induziert einen Strom in der rechten Spule.

Experiment: Versuch wie zuvor, aber statt des Leiters wird der Magnet bewegt.
Beobachtung: Das Voltmeter zeigt auch hier eine Induktionsspannung an.
Erklärung: Um die Spannung zu berechnen, müssen wir in ein Bezugssystem wechseln, in dem der Magnet ruht.

Experiment: Ein Magnetfeld wird an- bzw. ausgeschaltet. An einer im Magnetfeld befindlichen Spule wird die Spannung gemessen.
Beobachtung: Immer beim Schalten wird kurzzeitig eine Spannung induziert.

Unsere Erklärung mit der Lorentzkraft ist nicht anwendbar, da sich weder Magnet noch Spule bewegen. Wie können wir dieses Experiment erklären? Allen drei Experimenten ist gemeinsam, dass die Induktionsspannung auftritt, wenn sich das Feld im Innern der Spule ändert. Gesucht ist ein Induktionsgesetz, das alle drei Fälle erfasst. Idee: Es ändert sich der magnetische Fluss $\Phi$ , definiert als:

{\displaystyle \Phi

Eine Änderung des magnetischen Flusses $\Phi$ induziert eine Spannung. Probe am ersten Experiment (bewegte Leiterschleife):

U_{\rm {ind}}=d\cdot v\cdot B=d\cdot {\frac {\Delta s}{\Delta t}}\cdot B={\frac {d\Delta s}{\Delta t}}\cdot B={\frac {\Delta A}{\Delta t}}\cdot B={\frac {\Delta \Phi }{\Delta t}}

Im allgemeinen Fall gilt mit der Windungszahl $n$ (eine Begründung des Vorzeichens erfolgt später mit der Lenzschen Regel):

$U_{\rm {ind}}=-n\cdot \Phi '(t)=-n\cdot {\dot {\Phi }}$ ${\dot {\Phi }}=\left(B(t)\cdot A(t)\right)'={\dot {B}}\cdot A+B\cdot {\dot {A}}$ $[\Phi ]={\frac {\rm {Vs}}{\rm {m^{2}}}}\cdot {\rm {m^{2}={\rm {Vs}}}}$

Aufgabe: Eine Leiterschleife wird durch ein magnetisches Feld bewegt.

Wechselspannung

Sinusförmige Wechselspannung.
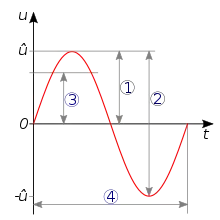
1 = Amplitude, auch Scheitelwert
2 = Spitze-Tal-Wert
3 = Effektivwert
4 = Periodendauer

Eine Leiterschleife dreht sich im Magnetfeld.

Experiment: Eine Leiterschleife wird mit konstanter Winkelgeschwindigkeit $\omega$ in einem Magnetfeld gedreht.
Beobachtung: Eine periodische Wechselspannung wird induziert.
Aufgabe: Berechne die Spannung $U_{\rm {ind}}(t)$ .

Idee: Die Fläche des Rähmchens senkrecht zu den Feldlinien ist relevant (“wirksame Fläche”).
Für diese gilt:

A_{n}=A\cdot \cos \varphi (t)=l\cdot b\cdot \cos \varphi (t)\,.

Für den Winkel $\varphi (t)$ gilt mit der konstanten Winkelgeschwindigkeit $\omega$ :

\varphi (t)=\omega \cdot t\,.

Für den magnetischen Fluss durch das Rähmchen erhalten wir:

\Phi (t)=B\cdot A_{\rm {n}}=B\cdot l\cdot b\cdot \cos \varphi (t)=B\cdot l\cdot b\cdot \cos(\omega \cdot t)\,.

Beschreiben wir die Fläche und ihre Orientierung im Raum durch einen Vektor ${\vec {A}}$ , der den Betrag des Flächeninhalts $\|{\vec {A}}\|=A=b\cdot l$ und die Richtung der Flächennormalen hat, so können wir in Vektorschreibweise den magnetischen Fluss $\Phi$ auch schreiben als: $\Phi ={\vec {B}}\cdot {\vec {A}}=\|{\vec {B}}\|\cdot \|{\vec {A}}\|\cdot \cos \varphi \,,$ mit dem Winkel $\varphi$ zwischen den Vektoren ${\vec {B}}$ und ${\vec {A}}$ .

Die Induktionsspannung an $n$ Windungen ist dann:

U_{\rm {ind}}=-n\cdot {\dot {\Phi }}(t)=-n\cdot B\cdot l\cdot b\cdot \left[\cos(\omega \cdot t)\right]'=\underbrace {n\cdot B\cdot l\cdot b\cdot \omega } _{=:\,{\hat {U}}_{\rm {ind}}}\cdot \sin(\omega \cdot t)\,.

Die maximale Induktionsspannung (Amplitude) der Wechselspannung bezeichnet man als ${\hat {U}}_{\rm {ind}}$ .

Aufgabe: Eine Leiterschleife dreht sich im magnetischen Feld.

Die Lenzsche Regel

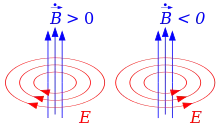
Das Prinzip der Lenzschen Regel: Ändert sich der magnetische Fluss, so wird er von einem elektrischen Wirbelfeld E umgeben, das, wenn möglich, einen der Flussänderung entgegenwirkenden Strom erzeugt.

Frage: Welche Richtung hat ein aufgrund der Induktionsspannung $U_{\rm {ind}}$ fließender Induktionsstrom?
Lösung: Er ist so gerichtet, dass die magnetische Kraft $F_{\rm {m}}$ die Bewegung bremst ( $\rightarrow$ Energieerhaltung).

Lenzsche Regel: Die Induktionsspannung ist stets so gepolt, dass sie durch einen von ihr erzeugten Strom der Ursache des Induktionsvorgangs entgegenwirken kann. Kurz: Der Induktionsstrom ist so gerichtet, dass er seiner Ursache entgegen wirkt.

Experiment: Permanentmagnet durch Alu-Rohr „fallen“ lassen.
Beobachtung: Der Magnet sinkt langsam durch das Rohr nach unten.
Erklärung: Im Alu-Rohr werden Ströme induziert, deren Magnetfeld den „fallenden“ Magneten verzögert.

Experiment: Gauss-Kanone.
Beobachtung: Beim Einschalten der Spule wird der Aluring nach oben geschleudert.
Erklärung: Im Alu-Ring wird ein Strom induziert, da sich der magnetische Fluss durch den Ring ändert. Dieser Strom wirkt nach der Lenzschen Regel seiner Ursache, dem Anstieg des Magnetfelds, entgegen, d.h. das vom induzierten Strom hervorgerufene Magnetfeld ist dem ursprünglichen Magnetfeld entgegegengerichtet. Es kommt zur Abstoßung.

Experiment: Spule mit Eisenjoch, dieses öffnen bzw. schließen.
Beobachtung: Wird der Eisenkern mit dem Joch geschlossen, so sinkt die Stromstärke kurzzeitig. Wir das Joch wieder geöffnet, so steigt die Stromstärke kurzzeitig an.
Erklärung: Durch das Schließen und Öffnen des Eisenkerns wird der magnetische Fluss durch die Spule größer bzw. kleiner. Es wird kurzzeitig eine Spannung induziert, die ihrer Ursache entgegenwirkt:

Schließen des Jochs: Die Ursache für die Induktionsspannung ist das Ansteigen des magnetischen Flusses. Folglich ist sie so gerichtet, dass der Strom kurzzeitig absinkt.
Öffnen des Jochs: Die Ursache für die Induktionsspannung ist die Verringerung des magnetischen Flusses. Folglich ist sie so gerichtet, dass der Strom kurzzeitig ansteigt.

ToDo Bilder/Skizzen

Selbstinduktion

Zeitverläufe zur Animation.

Animation: Selbstinduktion im Gleichstromkreis, nach dem Schließen des Tasters leuchtet S₂ etwas später auf als S₁.

Induktivität $L$ einer langen Spule

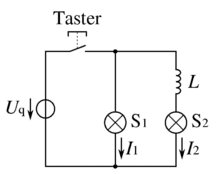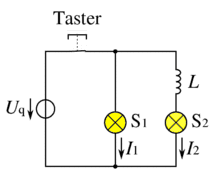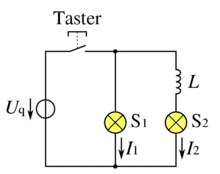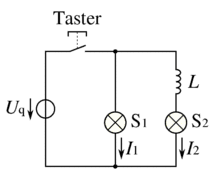
Experiment: Parallelschaltung von Spule und Lampe sowie Widerstand und Lampe, Einschaltvorgang.
Beobachtung: Wird der Stromkreis geschlossen, so leuchtet die Lampe nach dem Widerstand sofort, die Lampe nach der Spule verzögert auf.
Erklärung: Nach dem Einschalten steigt der magnetische Fluss durch die Spule an. An den Enden der Spule wird eine Spannung induziert, die sogenannte „Selbstinduktionsspannung“. Sie ist so gerichtet, dass sie ihrer Ursache, nämlich dem Ansteigen des Stroms und damit dem Ansteigen des magnetischen Flusses, entgegenwirkt. Dadurch verlangsamt sich der Anstieg des Stroms.

Leite eine Formel für die Selbstinduktionsspannung einer langen Spule her. Es gilt:

U_{\mathrm {ind} }=-n\cdot {\dot {\Phi }}=-n\cdot A\cdot {\dot {B}}\,.

Mit der Formel für das magnetische Feld im Innern einer langen Spule:

B=\mu _{0}\mu _{r}{\frac {n\cdot I(t)}{l}}

folgt:

U_{\mathrm {ind} }=-n\cdot A\cdot \mu _{0}\mu _{r}{\frac {n\cdot {\dot {I}}(t)}{l}}=-\underbrace {\frac {n^{2}\cdot A\cdot \mu _{0}\mu _{r}}{l}} _{=:L}\cdot {\dot {I}}(t)=-L{\dot {I}}(t)\,.

Dabei ist $L:=\mu _{0}\mu _{r}{\frac {n^{2}\cdot A}{l}}$ die Eigeninduktivität der langen Spule. $L$ hängt nur von der Bauart der Spule ab. Die Einheit der Eigeninduktivität $L$ ist:

[L]={\frac {\rm {m^{2}Vs}}{\rm {Am^{2}}}}={\frac {\rm {Vs}}{\rm {A}}}={\rm {H\quad {\text{Henry}}.}}

Jede Spule hat eine charakteristische Eigeninduktivität $L$ .

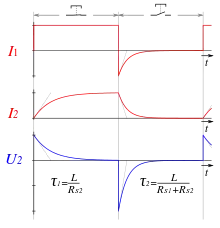
Einschalten einer Spule

Einschalten der Spule.

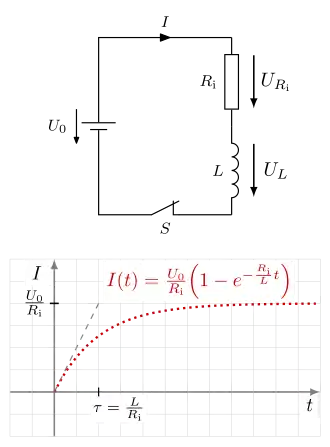
Im Folgenden bestimmen wir den zeitlichen Verlauf des Stroms $I(t)$ beim Einschalten einer Spule. Nach Anwendung der Maschenregel erhält man:

U_{0}=U_{R_{\mathrm {i} }}+U_{L}=R_{\mathrm {i} }\cdot I(t)+L\,{\dot {I}}(t)\,.

Daraus ergibt sich die Differentialgleichung (DGL) für $I(t)$ :

{\dot {I}}(t)={\frac {U_{0}-R_{\mathrm {i} }\cdot I(t)}{L}}\,.

Gesucht ist die Funktion $I(t)$ , die diese Differentialgleichung erfüllt. Außerdem muss im Moment des Einschaltens $t=0$ die Anfangsbedingung erfüllt sein:

I(0)=0\,.

Die schon daraus folgende Gleichung erlaubt die Induktivität einer Spule experimentell aus der Steigung von $I(t)$ für $t=0$ zu bestimmen:

{\dot {I}}(0)={\frac {U_{0}-R_{\mathrm {i} }\cdot I(0)}{L}}={\frac {U_{0}}{L}}\quad \implies \quad L={\frac {U_{0}}{{\dot {I}}(0)}}\,.

Nach hinreichend langer Zeit ändert sich der magnetische Fluss und damit $I(t)$ nicht mehr und es fließt dann der maximale Strom $I(\infty )$ :

{\dot {I}}(\infty )=0\quad \implies \quad I(\infty )={\frac {U_{0}}{R_{\mathrm {i} }}}\,.

Die gesuchte Lösung der DGL lautet:

$I(t)={\frac {U_{0}}{R_{\mathrm {i} }}}\left(1-e^{-{\frac {R_{\mathrm {i} }}{L}}t}\right)\,.$

Ausschalten einer Spule

Ausschalten der Spule.

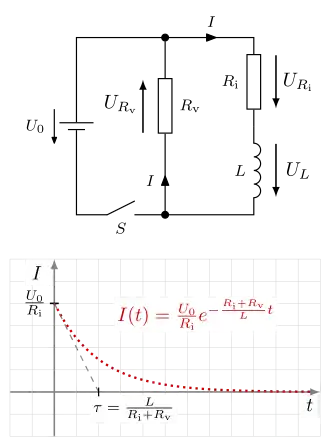
Beim Ausschalten fließt aufgrund der Selbstinduktion der Spule der Strom nach dem Ausschalten weiter. Wir leiten ihn über einen Schutzwiderstand $R_{\mathrm {v} }$ . Durch Anwendung der Maschenregel erhält man wieder eine Differentialgleichung (DGL):

0=U_{R_{\mathrm {v} }}+U_{R_{\mathrm {i} }}+U_{L}=\underbrace {(R_{\mathrm {v} }+R_{\mathrm {i} })} _{=:R}\cdot I(t)+L\,{\dot {I}}(t)\,,

\quad \implies \quad {\dot {I}}(t)=-{\frac {R}{L}}\cdot I(t)\,.

Im Moment des Ausschaltens $t=0$ gilt mit der Anfangsbedingung:

I(0)={\frac {U_{0}}{R_{\mathrm {i} }}}

die Beziehung:

{\dot {I}}(0)=-{\frac {R}{L}}\cdot I(0)=-{\frac {R}{L}}\cdot {\frac {U_{0}}{R_{\mathrm {i} }}}\,.

Die für $t=0$ an $R_{\mathrm {v} }$ anliegende (Induktions-) Spannung ist:

U_{R_{\mathrm {v} }}=R_{\mathrm {v} }\cdot I(0)=R_{\mathrm {v} }\cdot {\frac {U_{0}}{R_{\mathrm {i} }}}={\frac {R_{\mathrm {v} }}{R_{\mathrm {i} }}}\cdot U_{0}\,.

Man beachte, dass für $R_{\mathrm {v} }\gg R_{\mathrm {i} }$ diese Spannung viel größer als $U_{0}$ ist.

Die Lösung der DGL für den Ausschaltvorgang lautet:

$I(t)={\frac {U_{0}}{R_{\mathrm {i} }}}e^{-{\frac {R}{L}}t}\,,\qquad R:=R_{\mathrm {i} }+R_{\mathrm {v} }\,.$

Merke: Wird eine Spule ein- oder ausgeschaltet, so ändert sich der magnetische Fluss in der Spule. Es wird eine Spannung induziert, die aufgrund der Lenzschen Regel der Ursache der Flussänderung entgegenwirkt: Beim Einschalten wird das Ansteigen des Stroms verzögert, beim Ausschalten klingt der Strom verzögert ab.

Energie magnetischer Felder

Welche Energie ist in einer stromdurchflossenen Spule gespeichert? Wir betrachten die Leistung, die nach dem Ausschalten (also dem Abtrennen der Spannungsquelle) umgesetzt wird:

P(t)=U_{\mathrm {ind} }(t)\cdot I(t)=-L{\dot {I}}(t)\cdot I(t)\,.

Wir integrieren diese Leistung $P(t)$ , um die gesamte, der Spule entstammende Energie zu bestimmen:

W=\int _{0}^{\infty }-L{\dot {I}}(t)\cdot I(t)\,{\rm {{dt}=-{\frac {L}{2}}\int _{0}^{\infty }{\frac {\rm {d}}{\rm {dt}}}\left(I(t)^{2}\right)\,{\rm {{dt}=-{\frac {L}{2}}\left[I(t)^{2}\right]_{0}^{\infty }\,.}}}}

Zum Zeitpunkt $t=0$ fließt der Strom $I=I(0)$ , der dann exponentiell abfällt, d.h. $I(\infty )=0$ . Die Spule speichert also insgesamt die Energie:

$W={\frac {1}{2}}LI^{2}$

Diese Energie sitzt im magnetischen Feld der Spule. Wenn wir für $L$ die Formel der langen Spule einsetzen und den Strom durch die magnetische Feldstärke $B$ ausdrücken sowie für das Volumen der Spule $V=A\cdot l$ verwenden, ergibt sich:

W_{\mathrm {mag} }={\frac {1}{2}}{\frac {n^{2}\cdot A\cdot \mu _{0}\mu _{r}}{l}}I^{2}={\frac {n^{2}\cdot A\cdot \mu _{0}\mu _{r}}{2l}}\left({\frac {l\cdot B}{\mu _{0}\mu _{r}n}}\right)^{2}={\frac {A\cdot l\cdot B^{2}}{2\mu _{0}\mu _{r}}}={\frac {B^{2}}{2\mu _{0}\mu _{r}}}\cdot V

Für die Energiedichte des magnetischen Feldes $\rho _{\mathrm {mag} }={\frac {W_{\mathrm {mag} }}{V}}$ erhält man:

$\rho _{\mathrm {mag} }={\frac {B^{2}}{2\mu _{0}\mu _{r}}}$ .

Aufgabe: Herleitung durch Integration von $P=U\cdot I=R\cdot I^{2}$ .

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.