DEINE FESTE BEGLEITERIN
FÜR DIE SCHULMATHEMATIK
 EINFACH
VERSTÄNDLICH
AUFBAUEND		 GRATIS!*
UND SYMPATHISCH
JETZT STARTEN!
MIT MEHR ALS 200 THEORIE- UND AUFGABEN-ERKLÄRUNGSVIDEOS!
 Mathe lernen ist wie Fahrradfahren lernen: Du kannst es dir stundenlang erklären lassen, du wirst nie fahren können, wenn du nicht selber zu fahren probierst.
ACHTUNG!
Zumindest Aufgabe 1 von jedem Aufgabentyp probieren,
sie sind unterschiedlich!

Direkte Anwendung des Sinus und des Kosinussatzes


    1. In der folgenden Figur betragen die Seiten
      und die Winkel
      .

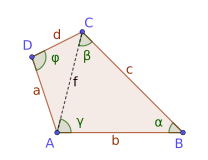
      Wie viel ist der Winkel ?

    2. Berechnen sie die Diagonalen des
      abgebildeten Deltoids, wenn die Seite , die Seite
      und der dazwischen liegende Winkel sind.

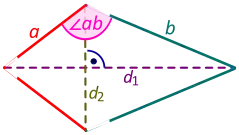
    3. In der folgenden Figur betragen die Seiten
      und die Winkel
      .

      Wie viel ist die Seite ?

    4. Berechnen sie die Diagonale des
      abgebildeten Deltoids, wenn die Seite , die Diagonale
      und der Winkel zwischen und sind.

    5. In der folgenden Figur betragen die Seiten
      und die Winkel
      .

      Wie viel ist die Seite ?

    6. Berechnen sie die Diagonale des
      abgebildeten Deltoids, wenn die Seite , die Seite
      und die Diagonale sind.

Vermessungsaufgaben


    1. Lisa beobachtet die Antenne auf dem Dach eines Gebäudes.
      Ihre Augen sind 1,73 m hoch, die Antenne selber ist 2,8 m hoch.
      Den unteren Rand der Antenne sieht Lisa unter
      einem Höhenwinkel von 67°, den oberen unter 74°.
      Wie weit vom Gebäude (genauer: vom "Fuß" der Antenne)
      befindet sich Lisa und wie hoch ist das Gebäude?
      Machen Sie eine saubere Skizze für die Berechnung!

    2. Vom Gipfel eines 1563 m hohen Berges wird der Abstand
      zwischen zwei Türmen in einem Tal gemessen,
      die sich beide auf einer Höhe von 548 m befinden.
      Zum ersten Turm wird der Tiefenwinkel gemessen
      und nach Schwenken des Messgerätes um den Horizontalwinkel
      zum anderen Turm wird dieser unter dem Tiefenwinkel
      gesehen. Wie viel ist der Abstand zwischen den Türmen?
      Machen Sie eine saubere Skizze für die Berechnung!

    3. Lisa beobachtet die Antenne auf dem Dach eines Gebäudes.
      Ihre Augen sind 1,25 m hoch, die Antenne selber ist 3,8 m hoch.
      Den unteren Rand der Antenne sieht Lisa unter
      einem Höhenwinkel von 77°, den oberen unter 80°.
      Wie weit vom Gebäude (genauer: vom "Fuß" der Antenne)
      befindet sich Lisa und wie hoch ist das Gebäude?
      Machen Sie eine saubere Skizze für die Berechnung!

    4. Vom Gipfel eines 2411 m hohen Berges wird der Abstand
      zwischen zwei Türmen in einem Tal gemessen,
      die sich beide auf einer Höhe von 356 m befinden.
      Zum ersten Turm wird der Tiefenwinkel gemessen
      und nach Schwenken des Messgerätes um den Horizontalwinkel
      zum anderen Turm wird dieser unter dem Tiefenwinkel
      gesehen. Wie viel ist der Abstand zwischen den Türmen?
      Machen Sie eine saubere Skizze für die Berechnung!

    5. Lisa beobachtet die Antenne auf dem Dach eines Gebäudes.
      Ihre Augen sind 0,95 m hoch, die Antenne selber ist 2,3 m hoch.
      Den unteren Rand der Antenne sieht Lisa unter
      einem Höhenwinkel von 70°, den oberen unter 74°.
      Wie weit vom Gebäude (genauer: vom "Fuß" der Antenne)
      befindet sich Lisa und wie hoch ist das Gebäude?
      Machen Sie eine saubere Skizze für die Berechnung!

    6. Vom Gipfel eines 1920 m hohen Berges wird der Abstand
      zwischen zwei Türmen in einem Tal gemessen,
      die sich beide auf einer Höhe von 1230 m befinden.
      Zum ersten Turm wird der Tiefenwinkel gemessen
      und nach Schwenken des Messgerätes um den Horizontalwinkel
      zum anderen Turm wird dieser unter dem Tiefenwinkel
      gesehen. Wie viel ist der Abstand zwischen den Türmen?
      Machen Sie eine saubere Skizze für die Berechnung!
This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.