| ||||||||||||||||
Zumindest Aufgabe 1 und 2 probieren,
sie sind unterschiedlich!
- y in Abhängigkeit von x
- Punkt (x|y), also erst x und dann y.
Lineare Funktion, also Gerade.
f(x) oder y ist die y-Achse (das y), x die x-Achse (das x).
d (bzw. n oder oder was auch immer nicht mit x multipliziert wird) ist der "Anfangswert", also der Wert der Funktion (y-Wert) da, wo x Null ist (y-Achsenabschnitt). Die Einheiten von d sind die Einheiten des y-Achse.
k (bzw. m oder s oder was auch immer mit x multipliziert wird) ist die Steigung der lineare Funktion. Wenn die Gerade eine Verbindung zwischen zwei Punkte in einem Liniendiagramm darstellt, dann sprechen wir von einer mittlere Änderungsrate. Die Steigung (z.B. k) ist positiv, wenn die Funktion nach oben geht, negativ wenn sie nach unten geht und Null wenn sie parallel zur x.Achse ist. y=d (z.B. y=4) bedeutet, dass die Steigung gleich Null ist, also die Gerade ist parallel zur x-Achse. Es gilt:
Die Einheiten der Steigung sind daher y-Einheiten pro eine x-Einheit.
Für die Funktion selber können wir beliebige Symbole benutzen, z.B.:
In diesem Beispiel steht A(h) als Ausdruck für die Abhängigkeit, also A (wofür in der Angabe A steht) in Abhängigkeit von h (wofür in der Angabe h steht). A(h) ist daher hier das y, h steht für das x. Mit h (also das Symbol für die x-Achse) wird hier d multipliziert, also ist d hier doch die Steigung. m wird zu diesem Produkt addiert, daher ist es der y-Achsenabschnitt ("Anfangswert").
In einem Punkt schreiben wir erst x und dann y (x|y). Um herauszufinden, ob drei oder mehrere Punkte zu einer und derselben Gerade gehören, können wir ggf. Tabellenkalkulation benutzen. Tabellenkalkulation benutzen wir bei der Regression.
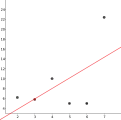
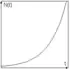
Die lineare Funktion kommt oft als Regressionsgerade vor. Der Korrelationskoeffizient (mit r angegeben) ist NICHT mit der Steigung zu verwechseln. Im ersten Bild sind die Punkte weit entfernt von der Gerade, im zweiten fast auf der Gerade, also im zweiten Fall ist der Koeffizient fast 1 (in diesem Fall allerdings −1, da fallend), im ersten Bild hingegen zwischen 0 und 1, aber näher zu 0,5. Man sagt: "Der lineare Zusammenhang zwischen (was auch immer auf den beiden Achsen steht) ist schwach (falls r nah zu 0) bzw. stark (im Gegenfall)". In Geogebra als r abzulesen, wenn man die Statistik (Symbol rechts oben im Diagramm) abruft, dafür ist die Gerade nicht notwendig.
Vergleich linearer und exponentieller Funktion:
| Lineare Funktion | Exponentialfunktion | |||
|---|---|---|---|---|
| Formel | ||||
| Im Text erkennen durch | Steigung der Gerade (in der Formel: s) Änderungsrate y-Einheiten PRO eine x-Einheit | Basis der Hochzahl (in der Formel: a) Relative Änderung ("Prozent"-Änderung) des y-Wertes bei Änderung des x-Wertes um 1 | ||
| Änderungsrate | Absolut (genauer Wert) | Relativ (Anteil, Prozent, -fach) | ||
| steigend ("nach oben") Wachstum | s>0 (positiv) | a>1 | ||
| fallend ("nach unten") Abnahme | s<0 (negativ) | 0<a<1 | ||
| y-Achsenabschnitt (i.d.R. "Anfangswert") | ||||
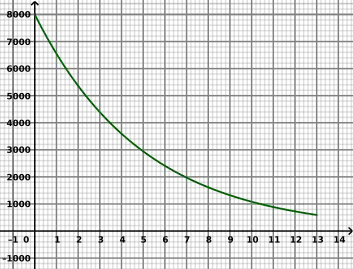
| Diagramme |
|
|
Aufgaben
-
Folgende Daten über das mittlere Gewicht in kg in Bezug auf das Alter in Jahren wurden erhoben:
- Stellen Sie die lineare Abhängigkeit des Gewichts vom Alter mit Hilfe einer Regressionsgerade dar (Funktion und Diagramm)!
- Was bedeutet der y-Achsenabschnitt in diesem Zusammenhang? Wie viel beträgt er? Ist das Sinnvoll?
- Stellen Sie mit Hilfe der Regressionsrechnung ein exponentielles Modell her! Was passt zu den Daten "besser", ein exponentielles oder ein lineares Modell? Warum?
- Stellen Sie die lineare Abhängigkeit des Gewichts von der Große mit Hilfe einer Regressionsgerade dar (Funktion und Diagramm)!
- Was zeigt uns die Steigung in diesem Zusammenhang?
- Wie viel soll das Gewicht einer 150 bzw. 160 cm große Person nach diesem linearen Modell sein?
- Wie können wir den Korrelationskoeffizient deuten und welchen Wert beträgt er? Gibt es hier eine Kausalität?
- Könnten folgende Daten ein lineares Modell repräsentieren?
Größe (cm): 165 168 170 Gewicht (kg): 63 66,5 67 - Tragen Sie die entsprechenden Werten in den Kästchen ein!
- Wie groß war das neugeborene Kind?
Alter 4 6 8 10 12 14 16 Gewicht 15,4 18,3 22,7 33,9 44,0 53,2 68,4
Für die gleiche Gruppe von Persone wurde die mittlere Größe in cm in Bezug auf das Alter in Jahren in der folgenden Tabelle erfasst:Alter 6 8 10 12 14 16 Größe 74,4 82,6 100,1 118,7 146,5 174,3
Die Größe eines Kindes in dm in Bezug auf sein Alter in Jahren wird von der nebenstehenden linearen Funktion angenähert. Nach dieser Funktion ist das Kind 2 Jahren nach seinem Geburt 4 dm groß und wächst pro 1,5 Jahre um 12 cm.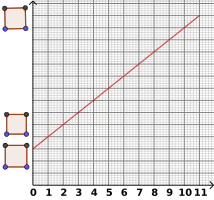
- Ein Zug hat 13 Wagons, manche mit 40 und der Rest mit 65 Sitzplätze. Insgesamt haben die Wagons 720 Sitzplätze. Wie viele Wagons mit 40 bzw. 65 Wagons gibt es?
- Stellen Sie die lineare Abhängigkeit der AbsolventInnen mit Hilfe einer Regressionsgerade dar (Funktion und Diagramm)! Wählen Sie für t=0 das Jahr 2001 (Sommer)!
- Was zeigt uns die Steigung in diesem Zusammenhang?
- Wie können wir den Korrelationskoeffizient deuten und welchen Wert beträgt er? Gibt es hier eine Kausalität?
- Wie viel ist der x-Achsenabschnitt und wie würden Sie ihn in diesen Zusammenhang interpretieren?
- Wann werden nach diesem linearen Modell die AbsolventInnen 21000 sein?
- Ist das Modell geeignet, wenn höchstens eine Abweichung von 6% vom tatsächlichen Wert im Jahr 2004 akzeptiert wird?
- Nehmen wir an, dass sich die Anzahl der AbsolventInnen nach einem linearen Modell je 4 Jahren um 2856 erhöht. Stimmen folgende Daten mit diesem Modell exakt überein?
Jahr: 2004 2006 2010 AbsolventInnen: 1500 2928 5784 - Tragen Sie die entsprechenden Werten in den Kästchen ein!
- Wie viele waren die AbsolventInnen im Jahr 2001?
Folgende Daten über die Anzahl der StudienabsolventInnen wurden erhoben:Jahr 2001 2004 2007 2010 2013 2016 2019 AbsolventInnen 2196 3550 6095 8969 11743 13705 16103
Die Anzahl der AbsolventInnen pro Jahr in einem Staat gemessen ab das Jahr 2001 wird von der nebenstehenden linearen Funktion angenähert. Nach dieser Funktion gab es im Jahr 2003 3000 AbsolventInnen und sie wuchsen um 2100 pro 3,5 Jahren.
-
Folgende Daten über den Einfluss der sexuellen Häufigkeit auf das Todesalter bei einer Gruppe von Männern wurden erhoben:
- Stellen Sie die lineare Abhängigkeit des Zusammenhangs mit Hilfe einer Regressionsgerade dar (Funktion und Diagramm)!
- Was bedeutet der y-Achsenabschnitt in diesem Zusammenhang? Wie viel beträgt er? Ist das Sinnvoll?
- Stellen Sie mit Hilfe der Regressionsrechnung ein exponentielles Modell her! Was passt zu den Daten "besser", ein exponentielles oder ein lineares Modell? Warum?
- Stellen Sie die lineare Abhängigkeit des Bierkonsums von der sexuellen Häufigkeit mit Hilfe einer Regressionsgerade dar (Funktion und Diagramm)!
- Was zeigt uns die Steigung in diesem Zusammenhang?
- Wie viel ist nach diesem linearen Modell die sexuelle Häufigkeit einer Person, die 4,2 Flaschen Bier pro Woche konsumiert?
- Wie können wir den Korrelationskoeffizient deuten und welchen Wert beträgt er? Gibt es hier eine Kausalität?
- Könnten folgende Daten ein lineares Modell repräsentieren?
Wöchentliche
Sexhäufigkeit2 3 5 Todesalter 73 74,5 77,2 - Tragen Sie die entsprechenden Werten in den Kästchen ein!
- Wie viel ist der Konsum bei Zölibat?
Wöchentliche
Sexhäufigkeit3 17 1 6 Todesalter 79 82 83 79 75 80
Folgende Daten über den möglichen Zusammenhang des Todesalters in Jahren in Bezug auf den Bierkonsum in Flaschen pro Woche bei der gleichen Gruppe von Männern wurden erhoben:Bierkonsum 2 3 2 8 6 5 Todesalter 79 82 83 79 75 80
Der Weinkonsum in Bezug auf die wöchentlichen sexuellen Häufigkeit wird von der nebenstehenden linearen Funktion angenähert. Nach dieser Funktion ist der Konsum 10,5 Gläser Wein, wenn man 4 mal in der Woche Sex hat und wächst um 3 Gläser, wenn man 2 mal mehr pro Woche Sex hat.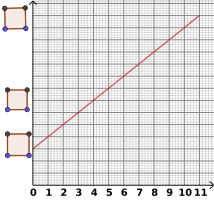
- Eine Flugzeugfirma hat 26 Flugzeuge, manche für 130 und der Rest für 150 Passagiere. Insgesamt kann die Firma 3680 Passagiere gleichzeitig bedienen. Wie viele Flugzeuge für 130 bzw. 150 Passagiere hat die Firma?
- Stellen Sie die lineare Abhängigkeit der Anzahl der täglich gerauchten Zigaretten von der Zeit mit Hilfe einer Regressionsgerade dar (Funktion und Diagramm)! Wählen Sie für t=0 das Jahr 2001!
- Was zeigt uns die Steigung in diesem Zusammenhang?
- Wie können wir den Korrelationskoeffizient deuten und welchen Wert beträgt er? Gibt es hier eine Kausalität?
- Was bedeutet der x-Achsenabschnitt in diesem Zusammenhang? Wie viel beträgt er? Ist das Sinnvoll?
- Welches Jahr sterben nach diesem linearen Modell Personen, die 40 Zigaretten rauchen?
- Ist das Modell geeignet, wenn höchstens eine Abweichung von 6% vom tatsächlichen Wert im Jahr 2004 akzeptiert wird?
- Nehmen wir an, dass sich die Anzahl der täglich gerauchten Zigaretten nach einem linearen Modell je 4 Jahren um 14,4 sinkt. Stimmen folgende Daten mit diesem Modell exakt überein?
Jahr: 2004 2007 2010 Zigaretten ∅: 28,2 39 49,8 - Tragen Sie die entsprechenden Werten in den Kästchen ein!
- Wie viel ist die Häufigkeit nach diesem Modell, wenn keine Zigarette geraucht wird?
Eine Kohortenstudie über Rauchen hat im Jahr 1935 geborenen Personen auf ihren Todesalter untersucht. Die durchschnittliche Anzahl der täglich gerauchten Zigaretten wurde ermittelt und in folgender Tabelle zusammengefasst.Jahr 2001 2004 2007 2010 2013 2016 2019 Zigaretten 35,4 30 25,1 19,8 15,3 9,9 5,2
Die Häufigkeit eines Herzanfalls in Bezug auf die Anzahl der täglich gerauchten Zigaretten wird von der nebenstehenden linearen Funktion angenähert. Nach dieser Funktion ist die Häufigkeit bei 4 Zigaretten am Tag 14% und steigt um 6% je 3 tägliche Zigarette.