Hoch

${\displaystyle {\color {white}\mathbf {MATHE} \mu \alpha T\mathbb {R} ix}}$ DEINE FESTE BEGLEITERIN FÜR DIE SCHULMATHEMATIK EINFACH VERSTÄNDLICH AUFBAUEND GRATIS!* UND SYMPATHISCH JETZT STARTEN! MIT MEHR ALS 200 THEORIE- UND AUFGABEN-ERKLÄRUNGSVIDEOS! Mathe lernen ist wie Fahrradfahren lernen: Du kannst es dir stundenlang erklären lassen, du wirst nie fahren können, wenn du nicht selber zu fahren probierst.

LINKS

Zumindest eine Aufgabe probieren

	lle	Gaben
	uf-

Theorie in Kürze (mit Geogebra)

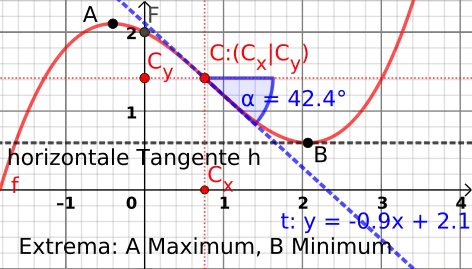
F ist der y-Achsenabschnitt, die Nullstelle −1,8 sehen wir (knapp) ganz links. Die Steigung der Funktion f (rot) am Punkt C bzw. an der Stelle C_x ist so viel, wie die Steigung der Tangente t (blau), also −0,9 oder auch so viel wie tan(α). Bei A und B (extrema) ist f´(x)=0

GeoGebra: Löse mit geschwungenen Klammern (und Beistriche zwischen den Gleichungen)!

• y in Abhängigkeit von x, y in Bezug auf x, je x desto y, bei Figuren oder so: y die Höhe und x der horizontale Abstand usw.

• Bei Kurvendiskussion Umkehraufgaben ist:
  • entweder ein Punkt gegeben:
    → Funktion selber benutzen
  • oder die Steigung (1. Ableitung):
    → 1. Ableitung benutzen

• Punkt (x|y)→ x und y gegeben
  • Punkt (x|y)
  • Wert der Funktion → (y) an der Stelle → (x)
  • Nullstelle a (a ist x, y ist Null)
  • y-Achsenabschnitt b → da, wo die y-Achse abgeschnitten wird, also der Abschnitt b ist y und x wird Null sein. Auch Anfangswert (der Funktion) genannt (nicht mit dem Wert "am Anfang" in Prozentrechnung verwechseln, der ist 100%).

• Steigung (Wenn 1 Punkt gegeben ist) :
  • 1. Ableitung = f´(x) (in Geogebra Funktion schreiben und das Symbol f´ benutzen)
  • "momentane Änderungsrate an der Stelle a ist c" oder
  • f´(a)=c:
    →f´(x) wird durch c ersetzt und x wird durch a (die Stelle a oder was im Klammer bei f´(a) steht) ersetzt
  • Winkel (f´(x) durch tan(Winkel) ersetzen)
  • Tangente (die Tangente t ist eine Gerade: t(x)= k⋅x+d. f´(x) durch die Steigung k dieser Gerade ersetzen)
  • knickfrei (gleiche Steigung)
  • Extrempunkt (oder Extremstelle) (und alles was „extrem“ bedeutet, also höchste, tiefste, kleinste usw.)
    → Steigung Null 0: f´(x) durch 0 ersetzen

• Steigung (Wenn 2 Punkte gegeben sind) :
  • mittlere Änderungsrate
  • Steigung einer Gerade
  • Differenzenquotient
  • ${\displaystyle k={\tfrac {\Delta y}{\Delta x}}}$ (k oder whatever Buchstabe für die Steigung der Gerade da steht)

• Intervall → x-Achse (wenn nichts anderes gesagt wird)

Aufgaben

1. 
   

   Eine quadratische Funktion geht durch die Punkte ${\displaystyle \ P_{1}:(3|5)\ }$ und ${\displaystyle \ P_{2}:(1{,}5|4{,}5)}$. Ihre Ableitung an der Stelle 2 ist null. Wie lautet die Funktion?

2. 
   

   Eine quadratische Funktion geht durch die Punkte ${\displaystyle \ P_{1}:(2|5)\ }$, ${\displaystyle \ P_{2}:(1{,}5|4{,}5)\ }$ und ${\displaystyle \ P_{3}:(0|-1)}$. Wie lautet die Funktion?

3. 
   

   Eine quadratische Funktion geht durch den Punkt ${\displaystyle P:(0|-1)}$. Der Wert der Funktion an der Stelle 2 ist 5, ihre Ableitung 0,4. Wie lautet die Funktion?

4. 
   

   Eine quadratische Funktion geht durch die Punkte ${\displaystyle \ P_{1}:(6|2)\ }$ und ${\displaystyle \ P_{2}:(3{,}5|7)}$. Ihre Ableitung an der Stelle 4 ist null. Wie lautet die Funktion?