Mathematrix: Aufgabensammlung/ Einheitskreis wichtige Punkte

{\color {white}\mathbf {MATHE} \mu \alpha T\mathbb {R} ix}

DEINE FESTE BEGLEITERIN
FÜR DIE SCHULMATHEMATIK

EINFACH
VERSTÄNDLICH
AUFBAUEND

GRATIS!^*
UND SYMPATHISCH
JETZT STARTEN!

MIT MEHR ALS 200 THEORIE- UND AUFGABEN-ERKLÄRUNGSVIDEOS!

Mathe lernen ist wie Fahrradfahren lernen: Du kannst es dir stundenlang erklären lassen, du wirst nie fahren können, wenn du nicht selber zu fahren probierst.

LINKS

Zumindest eine Aufgabe probieren

	lle	Gaben
	uf-

Theorie in Kürze (mit Geogebra)

Kreis, dessen Mittelpunkt sich am Anfang des (kartesischen) Koordinatensystems befindet und dessen Radius 1 ist. Der Winkel wird als Drehung im Bezug auf dem rechten Teil der x-Achse gemessen. Da der Radius 1 ist, ist der Umfang 2π. Das wird als Basis für die Winkeleinheit "Radiant" (Symbol: rad) benutzt. 360° Winkel ist so viel wie 2π rad.

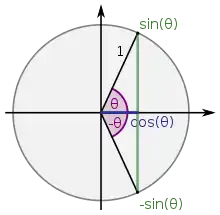Winkel mit gleichen Kosinus
$\omega \ {\text{und }}360^{\circ }-\omega$
Winkel mit gleichen Sinus
$\omega \ {\text{und }}180^{\circ }-\omega$
Winkel mit gleichen Sinus und Kosinus
$\omega \ {\text{und }}360^{\circ }+\omega$

Aufgaben

Beoboachten Sie die Figur und entscheiden Sie!

In welchem Quadrant des Kreises ist der Sinus,
der Kosinus und der Tangens positiv oder negativ?
Bei welchem Winkel ist der Sinus 0, 1 oder -1? Geben Sie diesen Winkel
sowohl in Grad als auch in Radiants an!

Beoboachten Sie die Figur und entscheiden Sie!

In welchem Quadrant des Kreises ist der Sinus,
der Kosinus und der Tangens positiv oder negativ?
Bei welchem Winkel ist der Sinus gleich dem
Kosinus und positiv? Wann ist der Kosinus 1/2?
Geben Sie vier Winkeln jeder Art sowohl in Grad
als auch in Radiants an!

Beoboachten Sie die Figur und entscheiden Sie!

In welchem Quadrant des Kreises ist der Sinus,
der Kosinus und der Tangens positiv oder negativ?
Bei welchem Winkel ist der Kosinus gleich 0, 1 oder −1?
Geben Sie vier Winkeln jeder Art sowohl in Grad
als auch in Radiants an!

Beoboachten Sie die Figur und entscheiden Sie!

In welchem Quadrant des Kreises ist der Sinus,
der Kosinus und der Tangens positiv oder negativ?
Bei welchem Winkel ist der Kosinus gleich ${\tfrac {1}{2}}$ oder $-{\tfrac {1}{2}}$ ?
Geben Sie vier Winkeln jeder Art sowohl in Grad
als auch in Radiants an!

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.