DEINE FESTE BEGLEITERIN
FÜR DIE SCHULMATHEMATIK
 EINFACH
VERSTÄNDLICH
AUFBAUEND		 GRATIS!*
UND SYMPATHISCH
JETZT STARTEN!
MIT MEHR ALS 200 THEORIE- UND AUFGABEN-ERKLÄRUNGSVIDEOS!
 Mathe lernen ist wie Fahrradfahren lernen: Du kannst es dir stundenlang erklären lassen, du wirst nie fahren können, wenn du nicht selber zu fahren probierst.
LINKS
ACHTUNG!
Zumindest Aufgabe 1 von Urnentyp und
1 bis 3 von Maturatyp probieren,
sie sind unterschiedlich!
Theorie in Kürze (mit Geogebra)


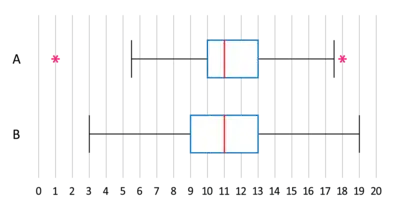
Die Daten sind eingeordnet. Die genauen Daten kann man nicht ablesen. Klar ist nur: die ein viertel kleinsten Werte befinden sich zwischen "Antenne" links (oder unten) und Anfang (links oder unten) des Rechtecks das sich irgendwo in der "Mitte" befindet; Diese linke (oder untere) Seite des Rechtecks ist das erste "Quartil". In diesem Rechteck und bis zur "Linie" irgendwo in seiner "Mitte" befindet sich das zweite viertel der eingeordneten Werte. Daher ist diese Linie (die nur in seltenen Fällen genau in der Mitte des Rechtecks ist) der Median (Zentralwert). Das dritte viertel befindet sich dann bis zur rechten (bzw. oberen) Seite des Rechtecks (drittes Quartil) und die größten viertel Werte sind darüber.

(Inter)Quartilabstand (IQR): Die Differenz der Werte an den Seiten des Rechtecks.

Spannweite (allgemein und nicht nur im boxplot): Maximum minus Minimum.

Möglicherweise gibt es "Ausreißer": Oft werden sie mit Hilfe des IQR definiert: ist der Wert links (einer der größten) mehr als das 1,5-fache des IQR als das dritte Quartil (rechte bzw obere Seite des Rechtecks), dann ist es ein Ausreißer.

Urne


    1. In einer Urne gibt es 5 schwarze und 4 rote Kugeln. Wir ziehen drei mal zufällig
      jeweils eine Kugel, ohne sie zurückzulegen. Wie viel ist die Wahrscheinlichkeit, dass:
    1. alle 3 Kugel rot sind?
    2. die ersten zwei schwarz und die dritte rot sind?
    3. wir zwei schwarze und eine rote Kugel ziehen?
    4. wir zwei rote und eine schwarze Kugel ziehen?
    5. das Letztere passiert, wenn wir doch zurücklegen?

    2. In einer Urne gibt es 9 schwarze und 5 rote Kugeln. Wir ziehen drei mal zufällig
      jeweils eine Kugel, ohne sie zurückzulegen. Wie viel ist die Wahrscheinlichkeit, dass:
    1. alle 3 Kugel rot sind?
    2. die ersten zwei schwarz und die dritte rot sind?
    3. wir zwei schwarze und eine rote Kugel ziehen?
    4. wir zwei rote und eine schwarze Kugel ziehen?
    5. das Letztere passiert, wenn wir doch zurücklegen?

    3. In einer Urne gibt es 2 schwarze und 11 rote Kugeln. Wir ziehen drei mal zufällig
      jeweils eine Kugel, ohne sie zurückzulegen. Wie viel ist die Wahrscheinlichkeit, dass:
    1. alle 3 Kugel rot sind?
    2. alle 3 Kugel schwarz sind?
    3. die ersten zwei schwarz und die dritte rot sind?
    4. wir zwei schwarze und eine rote Kugel ziehen?
    5. wir zwei rote und eine schwarze Kugel ziehen?
    6. das Letztere passiert, wenn wir doch zurücklegen?
    7. alle drei schwarz sind, wenn wir doch zurücklegen?

    4. In einer Urne gibt es 4 schwarze und 7 rote Kugeln. Wir ziehen drei mal zufällig
      jeweils eine Kugel, ohne sie zurückzulegen. Wie viel ist die Wahrscheinlichkeit, dass:
    1. alle 3 Kugel rot sind?
    2. alle 3 Kugel schwarz sind?
    3. die ersten zwei schwarz und die dritte rot sind?
    4. wir zwei schwarze und eine rote Kugel ziehen?
    5. wir zwei rote und eine schwarze Kugel ziehen?
    6. das Letztere passiert, wenn wir doch zurücklegen?
    7. alle drei schwarz sind, wenn wir doch zurücklegen?

Matura

ACHTUNG!
Zumindest Aufgabe 1 bis 5 probieren,
sie sind unterschiedlich!

    1. Es gibt 4 Hauptblutgruppen, A, B, 0 und AB. Die jeweiligen Häufigkeiten in einer bestimmten Region sind 31%, 14%, 43% und 12%. Es gibt dazu einige andere Blutgruppen, die bekannteste ist die Rhesus Gruppe (positiv oder negativ). 80% der Gruppe B sind Rhesus positiv, bei der restlichen Gruppen sind jeweils 82% positiv.
    1. Vervollständigen Sie das der Situation entsprechende nachstehende Diagramm!
    2. Beschreiben Sie das Ereignis, dessen Wahrscheinlichkeit durch berechnet wird!
    3. Beschreiben Sie das Ereignis, dessen Wahrscheinlichkeit durch berechnet wird!
    4. Beschreiben Sie das Ereignis, dessen Wahrscheinlichkeit durch berechnet wird!
    5. Berechnen Sie die Wahrscheinlichkeit, dass eine zufällig ausgewählte Person nicht B Rhesus negativ ist!

      6. Eine Variante eines Brettspiels läuft wie im Folgenden:
      Es wird mit einem fairen Würfel gespielt. Man rückt so viele Felder vor, wie die Augenzahl. Wenn allerdings die Augenzahl 4 ist, muss man genau noch ein mal würfeln. Die Zufallsvariable X beschreibt die Anzahl der Felder, die man vorrückt.
    6. Schreiben Sie alle mögliche Ergebnisse und die entsprechenden Wahrscheinlichkeiten in einer Tabelle auf!
    7. Was bedeutet in diesem Zusammenhang der Erwartungswert und wie viel ist er?

    2. Nehmen wir an, dass es in einer Urne eine unbekannte Anzahl c von Kugeln gibt, von denen 5 rot sind.
    1. Wie lautet die Formel (mit Hilfe von c) für die Wahrscheinlichkeit, dass eine Kugel nicht rot ist?
    2. Es wird zwei mal ohne bzw. mit zurücklegen gezogen. Erstellen Sie die entsprechenden Baumdiagramme!
    3. Die Wahrscheinlichkeit, dass im ersten Fall (ohne zurücklegen) genau eine rote Kugel gezogen wird, ist Wie viele sind die nicht roten Kugeln?

      4. Es wird 2 mal gewürfelt und die Augensumme berechnet
    4. Schreiben Sie in einer Tabelle alle mögliche Ergebnisse und die entsprechenden Wahrscheinlichkeiten auf! Benutzen Sie dafür erst ein geeignetes Diagramm!
    5. Was ist mehr, die Wahrscheinlichkeit, dass die Augensumme mindestens 5 und höchstens 8 ist oder das Gegenereignis?
    6. Sie wiederholen den Vorgang (2 mal würfeln) 7 mal. Wie viel ist die Wahrscheinlichkeit, dass eine Augensumme von höchstens 6 zumindest drei mal vorkommt?

    3. Ein elektronisches Gerät wird aus drei Elemente A, B und C gebaut. Die entsprechenden Wahrscheinlichkeiten, dass ein Element nicht funktioniert, sind 3%, 1,8% bzw. 1,2%.
    1. Beschreiben Sie das Ereignis, dessen Wahrscheinlichkeit durch berechnet wird!
    2. Wie viel ist die Wahrscheinlichkeit, dass zumindest 1 Element nicht funktioniert?
    3. Wie viel ist die Wahrscheinlichkeit, dass höchstens 1 Element nicht funktioniert?
    4. Wie viel ist die Wahrscheinlichkeit, dass höchstens 2 Elemente nicht funktionieren?
    5. Wie viel ist die Wahrscheinlichkeit, dass das Gerät funktioniert, wenn alle 3 Elemente notwendig sind? Warum ist diese Frage zur zweiten Frage relevant und welcher Zusammenhang besteht zwischen den in der zwei Fragen beschriebenen Ereignissen?
    6. Wir haben 55 elektronische Geräte. Welche ist die wahrscheinlichste Anzahl von defekten A Teile?
    7. Wir haben 55 elektronische Geräte. Wie viel ist die Wahrscheinlichkeit, dass wir höchstens 2 defekte B Teile haben?

    4. In einer Tute gibt es 7 Schokoladen, 4 von 20 g und 3 von 40 g. Es wird gezogen ohne Zurücklegen, bis insgesamt zumindest 60g vorhanden sind. Die Zufallsvariable Y zeigt wie oft es gezogen wird, bis zumindest 60 g vorhanden sind.
    1. Erstellen Sie das entsprechende Baumdiagramm!
    2. Schreiben Sie alle mögliche Ergebnisse und die entsprechenden Wahrscheinlichkeiten in einer Tabelle auf!
    3. Wie viel ist der Erwartungswert?

      4. Um ein Spiel zu beginnen gibt es folgenden Vorgang: Eine Person würfelt. Ist die Augenzahl 3 oder mehr, soll die nächste Person würfeln. Im Gegenfall darf die erste Person genau noch einmal würfeln. Ist die Summe der Augenzahlen 4 oder weniger, dann darf diese Person in der nächsten Runde mit dem Spiel anfangen, sonst ist die nächste Person dran.

    4. Erstellen Sie das entsprechende Baumdiagramm!
    5. Wie viel ist die Wahrscheinlichkeit für eine Person in einem Durchgang das Spiel anzufangen?
    6. 5 Personen spielen. Wie viel ist die Wahrscheinlichkeit, dass zumindest drei Personen im ersten Durchgang mit dem Spiel anfangen dürfen?
    7. Die Zufallsvariable R zeigt uns, wie viele Runden notwendig sind, damit eine Person mit dem Spiel beginnt. Wie viel ist der Erwartungswert von R?

    5. Die Prävalenz einer Krankheit (wie oft sie vorkommt) ist 25,5%. Die Sensitivität (Prozentsatz der positiven Ergebnissen, wenn eine Person krank ist) eines Tests dafür ist 99,6%, die Spezifität (Prozentsatz der negativen Ergebnissen, wenn eine Person gesund ist) 80%.
    1. Erstellen Sie das entsprechende Baumdiagramm!
    2. Berechnen Sie die Wahrscheinlichkeit, dass eine zufällig ausgewählte Person Gesund ist und einen positiven Test hat!
    3. Beschreiben Sie das Ereignis, dessen Wahrscheinlichkeit durch berechnet wird!
    4. Beschreiben Sie das Ereignis, dessen Wahrscheinlichkeit durch berschnet wird!
    5. Wie viel ist die Wahrscheinlichkeit beim positiven Test, dass die Person tatsächlich krank ist?

      6. Von einer Urne mit 4 schwarzen, 1 weiße, 1 rote und 2 grünen Kugeln wird zufällig jeweils eine Kugel ohne Zurücklegen gezogen, bis eine Schwarze vorkommt. Die Zufallsvariable Z beschreibt die Anzahl der Züge die notwendig sind.
    6. Schreiben Sie alle mögliche Ergebnisse und die entsprechenden Wahrscheinlichkeiten in einer Tabelle auf!
    7. Wie viel ist der Erwartungswert und wie viel das wahrscheinlichste Ergebnis?
    8. Berechnen Sie die Wahrscheinlichkeit, dass eine schwarze Kugel spätestens beim dritten Zug gezogen wird!
    9. Berechnen Sie die Wahrscheinlichkeit, dass eine schwarze Kugel frühestens beim zweiten Zug gezogen wird!

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.