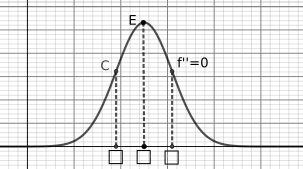Grundrechenarten und Bruchrechnungen
Definitionen der Grundrechenarten
Die vier Grundrechenarten
Mathematrix: Aufgabensammlung/ Die vier Grundrechenarten
Weitere Ausdrücke für die vier Grundrechenarten
Mathematrix: Aufgabensammlung/ Weitere Ausdrücke für die vier Grundrechenarten
Das Gleichheitszeichen
Mathematrix: Aufgabensammlung/ Das Gleichheitszeichen
Negative Zahlen
Mathematrix: Aufgabensammlung/ Negative Zahlen
Das Komma bei Dezimalzahlen
Mathematrix: Aufgabensammlung/ Das Komma bei Dezimalzahlen
Addition
Mathematrix: Aufgabensammlung/ Addition
Subtraktion
Mathematrix: Aufgabensammlung/ Subtraktion
Multiplikation
Definition der Multiplikation
Mathematrix: Aufgabensammlung/ Definition der Multiplikation
Multiplikation mit Hilfe der Einmaleins-Tabelle
Mathematrix: Aufgabensammlung/ Multiplikation mit Hilfe der Einmaleins-Tabelle
Multiplikation von Zahlen mit mehreren Ziffern und Nachkommastellen
Mathematrix: Aufgabensammlung/ Multiplikation von Zahlen mit mehreren Ziffern und Nachkommastellen
Division
Definition der Division
Mathematrix: Aufgabensammlung/ Definition der Division
Einfache Division mit Hilfe der Einmaleins-Tabelle
Mathematrix: Aufgabensammlung/ Einfache Division mit Hilfe der Einmaleins-Tabelle
Der Haupt(vor)gang der Division
Mathematrix: Aufgabensammlung/ Der Haupt(vor)gang
Dividend mit Nullen am Ende
Mathematrix: Aufgabensammlung/ Dividend mit Nullen am Ende
Null in der Mitte des Ergebnisses
Mathematrix: Aufgabensammlung/ Null in der Mitte des Ergebnisses
Null am Anfang des Ergebnisses
Mathematrix: Aufgabensammlung/ Null am Anfang des Ergebnisses
Dividend mit Komma (einfach)
Mathematrix: Aufgabensammlung/ Dividend mit Komma (einfach)
Divisor mit Komma (einfach)
Mathematrix: Aufgabensammlung/ Divisor mit Komma (einfach)
Dividend ohne Komma, Ergebnis mit Komma (mit Null Rest)
Mathematrix: Aufgabensammlung/ Dividend ohne Komma, Ergebnis mit Komma (nicht periodisch)
Dividend ohne Komma, Ergebnis mit Komma (periodisch)
Mathematrix: Aufgabensammlung/ Dividend ohne Komma, Ergebnis mit Komma (periodisch)
Kombinationen
Mathematrix: Aufgabensammlung/ Kombinationen
Punktrechnungen mit 10, 100, 1000 und so weiter
Mathematrix: Aufgabensammlung/ Punktrechnungen mit 10, 100, 1000 und so weiter
Textaufgaben zu den Grundrechenarten
|
Vorrang der Rechenarten
Grundrechenartenvorrang
Vorrang mit Klammern in Klammern
Vorrang von weiteren Rechenarten
Mathematrix: Aufgabensammlung/ Vorrang von weiteren Rechenarten
Bruchrechnungen
Bruch Definitionen
Mathematrix: Aufgabensammlung/ Bruch Definitionen
Gemischte Zahlen
|
Bruchkürzen
|
Strich und Punkt Bruchrechnungen
Doppelbrüche
Arbeiten mit ganzen Zahlen und Brüchen
Mathematrix: Aufgabensammlung/ Arbeiten mit ganzen Zahlen und Brüchen
Bruchrechnungen und Vorrang
Textaufgaben zu den Bruchrechnungen
|
Primfaktorzerlegung
Definitionen
Mathematrix: Aufgabensammlung/ Definitionen
Anwendungen
Kürzen mit Primfaktorzerlegung
Bruchstrichrechnungen mit Primfaktorzerlegung
Teilbarkeit
Mathematrix: Aufgabensammlung/ Teilbarkeit
Schluss und Prozentrechnung
Direkte Proportionalität
|
Indirekte Proportionalität
|
Vergleich direkter und indirekter Proportionalität
|
Prozentrechung Begriffe
Mathematrix: Aufgabensammlung/ Prozentrechung Begriffe
Grundaufgaben der Prozentrechnung
|
Vertiefende Aufgaben der Prozentrechnung
Prozentrechnung bei Wachstum oder Zerfall
|
Umkehraufgaben der Prozentrechnungv
|
Erklärung der Prozent- und Schlussrechnung
Mathematrix: Aufgabensammlung/ Erklärung der Prozent- und Schlussrechnung
Kombinationsaufgaben der Prozentrechnung
|
Prozentrechnung abstrakt
|
Umsatzsteuer (USt.) und Rabatt
Umsatzsteuer (USt.)
|
Rabatt
|
USt. und Rabatt Kombination
USt. und Rabatt Gegebener Anfangswert
|
Mathematrix: Werkzeuge/ Links |
USt. und Rabatt Gegebener Endwert
|
Zinsen und Kapitalertragssteuer (KESt.)
Zinsrechnung Begriffe
Mathematrix: Aufgabensammlung/ Zinsrechnung Begriffe
Zinsen
KESt., effektive Zinsen, Guthaben nach einem Jahr
|
Effektiver Zinssatz
Mathematrix: Aufgabensammlung/ Effektiver Zinssatz
Zinsen Umkehraufgaben
|
Zinsrechnung
|
Exponential und Logarithmus Funktion
Wachstums- und Zerfallsprozessen
Wachstum
|
Zerfall
|
Zinseszins
|
Mathematrix: Werkzeuge/ Links |
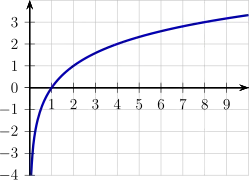
Exponentialfunktion und Logarithmus
|
Arbeiten mit Logarithmen
Rechenregeln zwischen Logarithmen
|
Exponentialfunktion Diagramm
|
Arbeiten mit Termen
Term Definition
Mathematrix: Aufgabensammlung/ Term Definition
Potenzen
Potenz Definition
Mathematrix: Aufgabensammlung/ Potenz Definition
Potenz Rechenarten
Strichrechnungen unter Potenzzahlen
Mathematrix: Aufgabensammlung/ Strichrechnungen unter Potenzzahlen
Punktrechnungen von zwei Potenzen mit der gleichen Basis
Schreiben Sie folgende Terme als eine Potenzzahl auf!
|
Potenzen mit negativer Hochzahl
|
Potenzen Erklärung
|
Potenz einer Potenzzahl
Mathematrix: Aufgabensammlung/ Potenz einer Potenzzahl
Potenzen mit Bruchhochzahl
Mathematrix: Aufgabensammlung/ Potenzen mit Bruchhochzahl
Potenz eines Produktes oder eines Bruches
Mathematrix: Aufgabensammlung/ Potenz eines Produktes oder eines Bruches
Arbeiten mit Potenzen: Die Rechenregel zusammengefasst
Mathematrix: Aufgabensammlung/ Arbeiten mit Potenzen: Die Rechenregel zusammengefasst
Komplexe Beispiele mit Potenzzahlen
|
Klammer Auflösen
Aufgaben mit einer Klammer
|
Aufgaben mit 2 Klammern
|
Ausmultiplizieren mit einer oder zwei Klammer
|
Mathematrix: Werkzeuge/ Links |
Arbeiten mit negativen Zahlen
Mathematrix: Aufgabensammlung/ Arbeiten mit negativen Zahlen
Herausheben
|
Binomische Formeln
Binomische Formeln ausmultiplizieren
|
Binomische Formeln faktorisieren
|
Binomische Formeln erkennen
|
Das pascalsche Dreieck Binompotenzen
|
Umformen Grundwissen Gegenrechnungen
|
Umformen einfache Kombinationen
|
Das Gleichheitszeichen in Umformungen
Mathematrix: Aufgabensammlung/ Das Gleichheitszeichen in Umformungen
Komplexe Umformungen
|
Bruchterme kürzen
|
Bruchterme in Brüchen mit gemeinsamen Nenner umwandeln
Mathematrix: Aufgabensammlung/ Bruchterme in Brüchen mit gemeinsamen Nenner umwandeln
Bruchtermegleichungen
|
Polynomdivision
Mathematrix: Aufgabensammlung/ Polynomdivision
Definitionsmenge
Mathematrix: Aufgabensammlung/ Definitionsmenge
Zahlendarstellungen Mengentheorie und Aussagenlogik
Zahlendarstellungen
(Dekadisches oder) Dezimalsystem
Darstellungen einer Zahl im Dezimalssystem
Mathematrix: Aufgabensammlung/ Darstellungen einer Zahl im Dezimalssystem
Die römische Zahlendarstellung
Die griechische Zahlendarstellung
Die Geschichte von Null
Binäre Zahlen
Weitere Zahlensysteme
Runden
Grundregeln des Rundens
Mathematrix: Aufgabensammlung/ Runden
Aufrunden von 9
Mathematrix: Aufgabensammlung/ Aufrunden von 9
Runden mit 5 als nächste Stelle
Mathematrix: Aufgabensammlung/ Runden mit 5 als nächste Stelle
Zahlenmengen
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Mengenlehre
Begriffe der Mengenlehre
Mathematrix: Aufgabensammlung/ Begriffe der Mengenlehre
Mengenlehre Aufgabebeispiel
|
Aussagenlogik
Aussagenlogik Theorie
Mathematrix: Aufgabensammlung/ Logische Aussage
Wahrheitstabellen
|
Mengenlehre und Aussagenlogik
|
Einheiten
Einheiten und physikalische Größen
|
||||||||||||||||||||||||||
Vorsätze von Einheiten
Mathematrix: Aufgabensammlung/ Vorsätze
Einheiten Umwandeln
Einheiten ohne Hochzahl
|
Einheiten mit Hochzahl
|
Komplexes Beispiel zur Umwandlung von Einheiten
|
Vorsilben Gleitkommadarstellung
Zahl in Gleitkommadarstellung umwandeln
Mathematrix: Aufgabensammlung/ Zahl in Gleitkommadarstellung umwandeln
Vorsilben und Gleitkommadarstellung
|
Statistik und Wahrscheinlichkeitsrechnung
Die Lageparameter
Lageparameter
|
Durchschnitt
Median
Modus
Vergleichen von Mittelwerten
|
Mittelwerte Argumentationsaufgaben
|
Streumaßen
Streuungsmaßen um den Durchschnitt (um das arithmetische Mittel)
Mathematrix: Aufgabensammlung/ Streuungsmaßen um das arithmetische Mittel
Streuungsmaßen um den Median (den Zentralwert)
|
Baumdiagramm
|
Wahrscheinlichkeitsverteilungen
Binomialverteilung
|
Normalverteilung
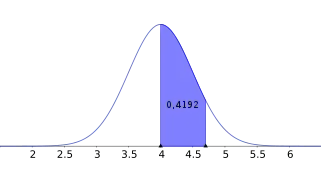
Anwendung der Normalverteilung bei gegebenen Erwartungswert und Standardabweichung
|
Anwendung der Normalverteilung bei gegebenen Grenzwerten
|
Normalverteilung und Funktionen
|
Satz von Bayes
Satz von Bayes konkretes Beispiel
|
Satz von Bayes abstraktes Beispiel
|
Regression Korrelation
|
Geometrische Konstruktionen
Dreieckskonstruktionen
Mathematrix: Aufgabensammlung/ Dreieckskonstruktionen
Die Klassische Probleme der antiken Mathematik
Quadratur des Kreises Versuche
Die Dreiteilung des Winkels
Die Würfelverdoppelung
Konstruktionen von regelmäßigen Vielecken
Das Regelmäßige Fünfeck und der goldene Schnitt
Geometrie der Ebene
Definitionen der ebenen Geometrie
Grundbegriffe der Geometrie
Mathematrix: Aufgabensammlung/ Grundbegriffe der Geometrie
Figuren
Mathematrix: Aufgabensammlung/ Figuren
Beweise von Formeln mancher ebenen Figuren
Anwendung der Formeln
Variablen in der Geometrie
Mathematrix: Aufgabensammlung/ Ebene Variablen
Formel Einsetzen in der ebenen Geometrie
|
Umformen in der ebenen Geometrie konkret
|
Umformen in der ebenen Geometrie abstrakt
|
Ähnlichkeit von Figuren
|
Zusammengesetzte Figuren
|
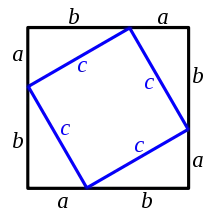
Satz von Pythagoras
|
Geometrie Beweise
|
Geometrie des Raums
Definitionen der RaumRaumgeometrie
Grundbegriffe der Raumgeometrie
Mathematrix: Aufgabensammlung/ Grundbegriffe der Raumgeometrie
Körper
Mathematrix: Aufgabensammlung/ Körper
Beweise von Formeln mancher Körpern
Mathematrix: Aufgabensammlung/ Beweise von Formeln mancher Körpern
Anwendung der Formeln
Variablen in der Raumgeometrie
Mathematrix: Aufgabensammlung/ Variablen in der Raumgeometrie
Formel Einsetzen in der Raumgeometrie
|
Umformen in der Raumgeometrie konkret
|
Umformen in der Raumgeometrie abstrakt
|
Ähnlichkeit von Körpern
Mathematrix: Aufgabensammlung/ Ähnlichkeit von Körpern
Zusammengesetzte Körper
Mathematrix: Aufgabensammlung/ Zusammengesetzte Körper
Diagramme
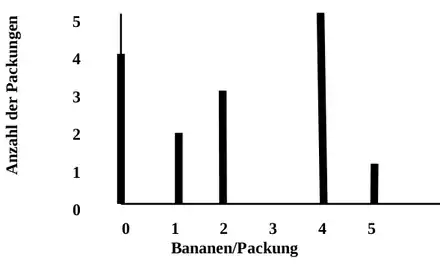
Säulendiagramm
|
Mittelwerte bei einem Säulendiagramm
|
Liniendiagramm
|
Lineare Funktion Diagramm
|
Kreisdiagramm
|
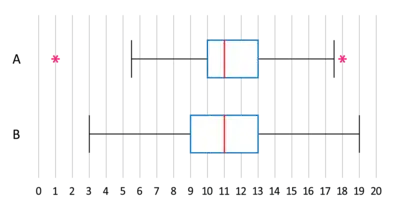
Boxplot
|
Funktionen
Funktion allgemein
Mathematrix: Aufgabensammlung/ Funktion allgemein
Lineare Funktion
Steigung und y Achsenabschnitt
Mathematrix: Aufgabensammlung/ Steigung und y Achsenabschnitt
Tabelle für eine lineare Funktion erstellen
Mathematrix: Aufgabensammlung/ Tabelle für eine lineare Funktion erstellen
Lineare Funktion Alltagsbeispiel
|
Diagramm einer linearen Funktion mit Hilfe von zwei Punkten erstellen
Mathematrix: Aufgabensammlung/ Diagramm einer linearen Funktion mit Hilfe von zwei Punkten erstellen
Eine lineare Funktion mit Hilfe von zwei Punkten ermitteln
|
Einheiten der Steigung
Mathematrix: Aufgabensammlung/ Einheiten der Steigung
Die Steigung und ihre Zusammenhänge
|
Textaufgaben zu den linearen Funktionen
|
Darstellungen der linearen Funktion
- Wie lautet die implizite und die Vektorform der
linearen Funktion ? - Wie lautet die explizite und die Vektorform der
linearen Funktion ? - Wie lautet die explizite und die implizite Form der
linearen Funktion ? - Berechnen Sie den Winkel zwischen den Geraden der zweiten und der dritten Funktion!
Lösung(en) einer Funktion
Mathematrix: Aufgabensammlung/ Lösung(en) einer Funktion
Schnittpunkte von Funktionen
Schnittpunkte von Funktionen in einem Diagramm
|
Schnittpunkte von Funktionen in einem Text
|
Die quadratische Funktion
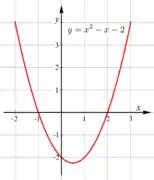
Die quadratische Gleichung
|
Quadratische Gleichung Textaufgaben
|
Quadratische Funktion Vertiefung
|
Polynomfunktionen Diagramm
|
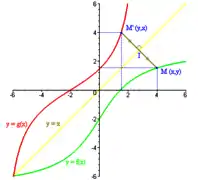
Umkehrfunktionen mit Umformen finden
|
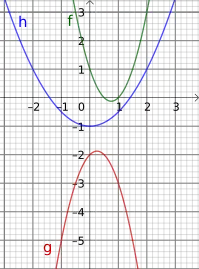
Funktionserkennung in Diagramm und Text
Funktionserkennung in Diagramm
|
Funktionsdiagramme Eigenschaften erkennen
|
Funktionserkennung in Text
|
||||||||||
Lineare Gleichungssysteme
Lineare Gleichungssysteme mit 2 Variablen
Einsetzungsverfahren
|
Gleichsetzungsverfahren
|
Additionsverfahren
|
Graphische Lösung eines linearen Gleichungssystems
Mathematrix: Aufgabensammlung/ Graphische Lösung eines linearen Gleichungssystems
Lineare Gleichungssysteme mit 2 Variablen
|
Lösungsmenge eines linearen Gleichungssystems
Lösbarkeit eines linearen Gleichungssystems mit 2 Variablen
Textaufgaben linearer Gleichungssysteme mit 2 Variablen
|
Lineare Gleichungssysteme mehrerer Variablen
Das gaußsche Eliminationsverfahren
Mathematrix: Aufgabensammlung/ Das gaußsche Eliminationsverfahren
Textaufgaben zu linearen Gleichungssystemen
|
Lösbarkeit von linearen Gleichungssystemen
Mathematrix: Aufgabensammlung/ Lösbarkeit von linearen Gleichungssystemen
Trigonometrische Funktionen
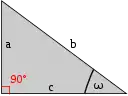
Definition von Sinus Kosinus und Tangens
|
Trigonometrische Satz von Pythagoras
Pythagoras Satz in Trigonometrie Abstrakt
|
Pythagoras Satz in Trigonometrie Konkret
|
Trigonometrische Umkehrfunktionen
|
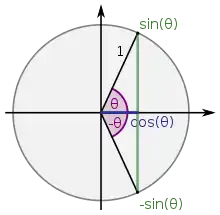
Einheitskreis
Einheitskreis und trigonometrische Funktionen
|
Radiant
|
Einheitskreis wichtige Punkte
|
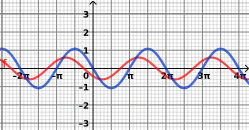
Trigonometrische Funktionen Diagramm
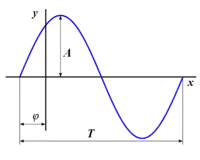
Parameter im Diagramm der Sinusfunktion
|
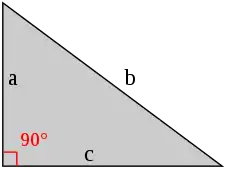
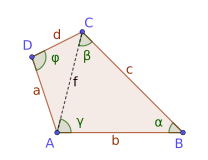
Sinus und Kosinussatz
Direkte Anwendung des Sinus und des Kosinussatzes
|
Vermessungsaufgaben
|
Vektoren
Vektor und Punkt
Mathematrix: Aufgabensammlung/ Vektor und Punkt
Vektoraddition
Mathematrix: Aufgabensammlung/ Vektoraddition
Vektor mit Zahl multiplizieren
Mathematrix: Aufgabensammlung/ Vektor mit Zahl multiplizieren
Betrag eines Vektors
Mathematrix: Aufgabensammlung/ Betrag eines Vektors
Richtung eines Vektors und Steigung
Mathematrix: Aufgabensammlung/ Richtung eines Vektors und Steigung
Zerlegung eines Vektors zu seinen Komponenten
Mathematrix: Aufgabensammlung/ Zerlegung eines Vektors zu seinen Komponenten
Skalarprodukt von Vektoren
Mathematrix: Aufgabensammlung/ Skalarprodukt von Vektoren
Winkelmaß zwischen zwei Vektoren
Mathematrix: Aufgabensammlung/ Winkelmaß zwischen zwei Vektoren
Orthogonalitätskriterium zwei Vektoren
Mathematrix: Aufgabensammlung/ Orthogonalitätskriterium zwei Vektoren
Vektorrechnungen
|
Differentialrechnung
Differenzenquotient
Grenzwerte
Die Ableitung einer Funktion
Die Ableitung als Steigung einer Funktion
|
Einheiten der Ableitung
Mathematrix: Aufgabensammlung/ Einheiten der Ableitung
Ableitung und Grenzwerten
|
Ableitung von Potenzfunktionen
|
Ableitung von Potenzfunktionen komplex
|
Ableitung von Potenzfunktionen schwierig
|
Ableitungen von weiteren Funktionen
|
Weitere Ableitungsregeln
Ableitungsregeln
|
Die Kettenregel
Mathematrix: Aufgabensammlung/ Die Kettenregel
Die Produktregel
Mathematrix: Aufgabensammlung/ Die Produktregel
Die Quotientenregel
Mathematrix: Aufgabensammlung/ Die Quotientenregel
Kurvendiskussion
Ermittlung einer quadratischen Funktion
|
Kurvendiskussion
|
Kurvendiskussion Umkehraufgaben
|
Integralrechnung
Integral von Potenzfunktionen
|
Integrale von weiteren Funktionen
|
Fläche zwischen zwei Funktionen
|
Rotationskörper
|
Rotationsfläche
Mathematrix: Aufgabensammlung/ Rotationsfläche
Folgen
Folgen
|