Formelsammlung Mathematik: Vektorrechnung

↑ Formelsammlung Mathematik

Koordinatenraum

Standardbasis

	Standardbasis
In der Ebene	${\vec {e}}_{x}={\begin{bmatrix}1\\0\end{bmatrix}},\;{\vec {e}}_{y}={\begin{bmatrix}0\\1\end{bmatrix}}$
Im Raum	${\vec {e}}_{x}={\begin{bmatrix}1\\0\\0\end{bmatrix}},\;{\vec {e}}_{y}={\begin{bmatrix}0\\1\\0\end{bmatrix}},\;{\vec {e}}_{z}={\begin{bmatrix}0\\0\\1\end{bmatrix}}$

Jeder Vektor lässt sich als Linearkombination der Basisvektoren der Standardbasis darstellen:

In der Ebene	${\vec {a}}={\begin{bmatrix}a_{x}\\a_{y}\end{bmatrix}}=a_{x}{\vec {e}}_{x}+a_{y}{\vec {e}}_{y}$
Im Raum	${\vec {a}}={\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}=a_{x}{\vec {e}}_{x}+a_{y}{\vec {e}}_{y}+a_{z}{\vec {e}}_{z}$

Operationen

Addition und Subtraktion

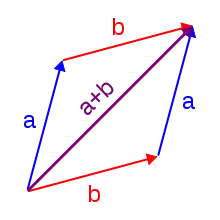
Geometrische Konstruktion der Addition von zwei Vektoren.

	Addition	Subtraktion
In der Ebene	${\vec {a}}+{\vec {b}}={\begin{bmatrix}a_{x}\\a_{y}\end{bmatrix}}+{\begin{bmatrix}b_{x}\\b_{y}\end{bmatrix}}={\begin{bmatrix}a_{x}+b_{x}\\a_{y}+b_{y}\end{bmatrix}}$	${\vec {a}}-{\vec {b}}={\begin{bmatrix}a_{x}\\a_{y}\end{bmatrix}}-{\begin{bmatrix}b_{x}\\b_{y}\end{bmatrix}}={\begin{bmatrix}a_{x}-b_{x}\\a_{y}-b_{y}\end{bmatrix}}$
Im Raum	${\vec {a}}+{\vec {b}}={\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}+{\begin{bmatrix}b_{x}\\b_{y}\\b_{z}\end{bmatrix}}={\begin{bmatrix}a_{x}+b_{x}\\a_{y}+b_{y}\\a_{z}+b_{z}\end{bmatrix}}$	${\vec {a}}-{\vec {b}}={\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}-{\begin{bmatrix}b_{x}\\b_{y}\\b_{z}\end{bmatrix}}={\begin{bmatrix}a_{x}-b_{x}\\a_{y}-b_{y}\\a_{z}-b_{z}\end{bmatrix}}$

Rechenregeln für ${\vec {a}},{\vec {b}},{\vec {c}}\in \mathbb {R} ^{n}$ :

Regel	Bezeichnung
${\vec {a}}+{\vec {b}}={\vec {b}}+{\vec {a}}$	Kommutativgesetz
${\vec {a}}+({\vec {b}}+{\vec {c}})=({\vec {a}}+{\vec {b}})+{\vec {c}}$	Assoziativgesetz

Eigenschaften	In Worten
${\vec {a}}+{\vec {0}}={\vec {a}}$	Der Nullvektor ist das neutrale Element der Addition.
${\vec {a}}+(-{\vec {b}})={\vec {a}}-{\vec {b}}$	Die Addition des additiv inversen Vektors zu ${\vec {b}}$ ist das Gleiche wie die Subtraktion von ${\vec {b}}$ .
${\vec {a}}+(-{\vec {a}})={\vec {0}}$	Die Addition des additiv inversen Vektors ergibt den Nullvektor.

Skalarmultiplikation

	Skalarmultiplikation
In der Ebene	$r{\vec {a}}=r{\begin{bmatrix}a_{x}\\a_{y}\end{bmatrix}}={\begin{bmatrix}ra_{x}\\ra_{y}\end{bmatrix}}$
Im Raum	$r{\vec {a}}=r{\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}={\begin{bmatrix}ra_{x}\\ra_{y}\\ra_{z}\end{bmatrix}}$

Rechenregeln für ${\vec {a}},{\vec {b}}\in \mathbb {R} ^{n}$ und $r,s\in \mathbb {R}$ :

Regel	Bezeichnung
$r({\vec {a}}+{\vec {b}})=r{\vec {a}}+r{\vec {b}}$	Distributivgesetz (Additivität)
$(r+s){\vec {a}}=r{\vec {a}}+s{\vec {a}}$	Distributivgesetz
$(rs){\vec {a}}=r(s{\vec {a}})$	Assoziativgesetz

Eigenschaften	In Worten
$1{\vec {a}}={\vec {a}}$	Multiplikation mit eins bewirkt nichts.
$0{\vec {a}}={\vec {0}}$	Multiplikation mit null ergibt den Nullvektor.
$(-1){\vec {a}}=-{\vec {a}}$	Multiplikation mit −1 ergibt den additiv inversen Vektor, der genau in die entgegengesetzte Richtung zeigt.
$2{\vec {a}}={\vec {a}}+{\vec {a}}$	Addition mit sich selbst ergibt eine Multiplikation mit einer natürlichen Zahl.
$3{\vec {a}}={\vec {a}}+{\vec {a}}+{\vec {a}}$
usw.

Skalarprodukt

	Skalarprodukt
In der Ebene	$\langle {\vec {a}},{\vec {b}}\rangle =\langle {\begin{bmatrix}a_{x}\\a_{y}\end{bmatrix}},{\begin{bmatrix}b_{x}\\b_{y}\end{bmatrix}}\rangle =a_{x}b_{x}+a_{y}b_{y}$
Im Raum	$\langle {\vec {a}},{\vec {b}}\rangle =\langle {\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}},{\begin{bmatrix}b_{x}\\b_{y}\\b_{z}\end{bmatrix}}\rangle =a_{x}b_{x}+a_{y}b_{y}+a_{z}b_{z}$

Rechenregeln für ${\vec {a}},{\vec {b}},{\vec {c}}\in \mathbb {R} ^{n}$ und $r\in \mathbb {R}$ :

\langle {\vec {a}},{\vec {b}}+{\vec {c}}\rangle =\langle {\vec {a}},{\vec {b}}\rangle +\langle {\vec {a}},{\vec {c}}\rangle

,

\langle {\vec {a}}+{\vec {b}},{\vec {c}}\rangle =\langle {\vec {a}},{\vec {c}}\rangle +\langle {\vec {b}},{\vec {c}}\rangle

,

r\langle {\vec {a}},{\vec {b}}\rangle =\langle r{\vec {a}},{\vec {b}}\rangle =\langle {\vec {a}},r{\vec {b}}\rangle

,

\langle {\vec {a}},{\vec {b}}\rangle =\langle {\vec {b}},{\vec {a}}\rangle

.

Die folgende Eigenschaft ist definierend für das Skalarprodukt:

\langle {\vec {a}},{\vec {b}}\rangle =|{\vec {a}}|\,|{\vec {b}}|\,\cos \varphi .\quad (\varphi =\angle ({\vec {a}},{\vec {b}}))

Betrag

	Betrag eines Vektors
In der Ebene	$\|{\vec {a}}\|:={\sqrt {\langle {\vec {a}},{\vec {a}}\rangle }}={\sqrt {a_{x}^{2}+a_{y}^{2}}}$
Im Raum	$\|{\vec {a}}\|:={\sqrt {\langle {\vec {a}},{\vec {a}}\rangle }}={\sqrt {a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}}$

	Einheitsvektor in Richtung von ${\vec {a}}$
In der Ebene	${\hat {a}}:={\frac {\vec {a}}{\|{\vec {a}}\|}}={\frac {1}{\|{\vec {a}}\|}}(a_{x}{\vec {e}}_{x}+a_{y}{\vec {e}}_{y})={\frac {a_{x}}{\|{\vec {a}}\|}}{\vec {e}}_{x}+{\frac {a_{y}}{\|{\vec {a}}\|}}{\vec {e}}_{y}$
Im Raum	${\hat {a}}:={\frac {\vec {a}}{\|{\vec {a}}\|}}={\frac {1}{\|{\vec {a}}\|}}(a_{x}{\vec {e}}_{x}+a_{y}{\vec {e}}_{y}+a_{z}{\vec {e}}_{z})={\frac {a_{x}}{\|{\vec {a}}\|}}{\vec {e}}_{x}+{\frac {a_{y}}{\|{\vec {a}}\|}}{\vec {e}}_{y}+{\frac {a_{z}}{\|{\vec {a}}\|}}{\vec {e}}_{z}$

Äußeres Produkt

In der Ebene
${\vec {a}}\wedge {\vec {b}}={\begin{bmatrix}a_{x}\\a_{y}\end{bmatrix}}\wedge {\begin{bmatrix}b_{x}\\b_{y}\end{bmatrix}}={\begin{vmatrix}a_{x}&b_{x}\\a_{y}&b_{y}\end{vmatrix}}\;{\vec {e}}_{x}\wedge {\vec {e}}_{y}=(a_{x}b_{y}-a_{y}b_{x})\,{\vec {e}}_{x}\wedge {\vec {e}}_{y}$

Im Raum
${\vec {a}}\wedge {\vec {b}}={\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}\wedge {\begin{bmatrix}b_{x}\\b_{y}\\b_{z}\end{bmatrix}}={\begin{vmatrix}a_{x}&b_{x}\\a_{y}&b_{y}\end{vmatrix}}\;{\vec {e}}_{x}\wedge {\vec {e}}_{y}+{\begin{vmatrix}a_{x}&b_{x}\\a_{z}&b_{z}\end{vmatrix}}\;{\vec {e}}_{x}\wedge {\vec {e}}_{z}+{\begin{vmatrix}a_{y}&b_{y}\\a_{z}&b_{z}\end{vmatrix}}\;{\vec {e}}_{y}\wedge {\vec {e}}_{z}$
${\vec {a}}\wedge {\vec {b}}\wedge {\vec {c}}={\begin{vmatrix}a_{x}&b_{x}&c_{x}\\a_{y}&b_{y}&c_{y}\\a_{z}&b_{z}&c_{z}\end{vmatrix}}\;{\vec {e}}_{x}\wedge {\vec {e}}_{y}\wedge {\vec {e}}_{z}={\bigg (}a_{x}{\begin{bmatrix}b_{y}&c_{y}\\b_{z}&c_{z}\end{bmatrix}}-a_{y}{\begin{bmatrix}b_{x}&c_{x}\\b_{z}&c_{z}\end{bmatrix}}+a_{z}{\begin{vmatrix}b_{x}&c_{x}\\b_{y}&c_{y}\end{vmatrix}}{\bigg )}\;{\vec {e}}_{x}\wedge {\vec {e}}_{y}\wedge {\vec {e}}_{z}$

Rechenregeln für ${\vec {a}},{\vec {b}},{\vec {c}}\in \mathbb {R} ^{n}$ und $r\in \mathbb {R}$ :

Regel	Bezeichnung
${\vec {a}}\wedge ({\vec {b}}+{\vec {c}})={\vec {a}}\wedge {\vec {b}}+{\vec {a}}\wedge {\vec {c}}$	Additivität
$({\vec {a}}+{\vec {b}})\wedge {\vec {c}}={\vec {a}}\wedge {\vec {c}}+{\vec {b}}\wedge {\vec {c}}$	Additivität
$r({\vec {a}}\wedge {\vec {b}})=(r{\vec {a}})\wedge {\vec {b}}={\vec {a}}\wedge (r{\vec {b}})$	Homogenität
${\vec {a}}\wedge {\vec {b}}=-{\vec {b}}\wedge {\vec {a}}$	Antikommutativgesetz
$({\vec {a}}\wedge {\vec {b}})\wedge {\vec {c}}={\vec {a}}\wedge ({\vec {b}}\wedge {\vec {c}})$	Assoziativgesetz

Eigenschaft
${\vec {a}}\wedge {\vec {a}}=0$
${\vec {a}}\wedge {\vec {0}}=0$

Kriterium für lineare Abhängigkeit
Für zwei Vektoren gilt: ${\vec {a}}\wedge {\vec {b}}=0$ genau dann, wenn ${\vec {a}}$ und ${\vec {b}}$ kollinear sind. Für drei Vektoren gilt: ${\vec {a}}\wedge {\vec {b}}\wedge {\vec {c}}=0$ genau dann, wenn ${\vec {a}},{\vec {b}},{\vec {c}}$ komplanar sind. Im $\mathbb {R} ^{3}$ gilt dabei: ${\vec {a}}\wedge {\vec {b}}\wedge {\vec {c}}=0$ genau dann, wenn $\det({\vec {a}},{\vec {b}},{\vec {c}})=0.$

Definition. Skalarprodukt von Bivektor-Produkten
In der Ebene	$\langle {\vec {a}}\wedge {\vec {b}},{\vec {c}}\wedge {\vec {d}}\rangle :=(a_{x}b_{y}-a_{y}b_{x})(c_{x}d_{y}-c_{y}d_{x})$
Im Raum	$\langle {\vec {a}}\wedge {\vec {b}},{\vec {c}}\wedge {\vec {d}}\rangle :=(a_{x}b_{y}-a_{y}b_{x})(c_{x}d_{y}-c_{y}d_{x})+(a_{x}b_{z}-a_{z}b_{x})(c_{x}d_{z}-c_{z}d_{x})+(a_{y}b_{z}-a_{z}b_{y})(c_{y}d_{z}-c_{z}d_{y})$
Allgemein	$\langle {\vec {a}}\wedge {\vec {b}},{\vec {c}}\wedge {\vec {d}}\rangle :=\sum _{1\leq i<j\leq n}(a_{i}b_{j}-a_{j}b_{i})(c_{i}d_{j}-c_{j}d_{i})$

Betrag:

|{\vec {a}}\wedge {\vec {b}}|:={\sqrt {\langle {\vec {a}}\wedge {\vec {b}},{\vec {a}}\wedge {\vec {b}}\rangle }}.

Für den Betrag gilt:

|{\vec {a}}\wedge {\vec {b}}|=|{\vec {a}}|\;|{\vec {b}}|\;\sin \varphi .\quad (\varphi =\angle ({\vec {a}},{\vec {b}}))

Cauchy-Binet-Identität:

\langle {\vec {a}}\wedge {\vec {b}},{\vec {c}}\wedge {\vec {d}}\rangle =\langle {\vec {a}},{\vec {c}}\rangle \langle {\vec {b}},{\vec {d}}\rangle -\langle {\vec {b}},{\vec {c}}\rangle \langle {\vec {a}},{\vec {d}}\rangle .

Lagrange-Identität:

|{\vec {a}}\wedge {\vec {b}}|^{2}=|{\vec {a}}|^{2}\;|{\vec {b}}|^{2}-\langle {\vec {a}},{\vec {b}}\rangle ^{2}.

Im Gegensatz zum Vektorprodukt gelten die Regeln für ${\vec {a}},{\vec {b}},{\vec {c}},{\vec {d}}\in \mathbb {R} ^{n}$ , auch wenn n≠3.

Vektorprodukt

	Vektorprodukt
(In der Ebene)	${\vec {a}}\times {\vec {b}}={\begin{bmatrix}a_{x}\\a_{y}\\0\end{bmatrix}}\times {\begin{bmatrix}b_{x}\\b_{y}\\0\end{bmatrix}}={\begin{bmatrix}0\\0\\a_{x}b_{y}-a_{y}b_{x}\end{bmatrix}}$
Im Raum	${\vec {a}}\times {\vec {b}}={\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}\times {\begin{bmatrix}b_{x}\\b_{y}\\b_{z}\end{bmatrix}}={\begin{vmatrix}{\vec {e}}_{x}&a_{x}&b_{x}\\{\vec {e}}_{y}&a_{y}&b_{y}\\{\vec {e}}_{z}&a_{z}&b_{z}\end{vmatrix}}={\begin{bmatrix}a_{y}b_{z}-a_{z}b_{y}\\a_{z}b_{x}-a_{x}b_{z}\\a_{x}b_{y}-a_{y}b_{x}\end{bmatrix}}$

Rechenregeln für ${\vec {a}},{\vec {b}},{\vec {c}}\in \mathbb {R} ^{3}$ und $r\in \mathbb {R}$ :

{\vec {a}}\times ({\vec {b}}+{\vec {c}})={\vec {a}}\times {\vec {b}}+{\vec {a}}\times {\vec {c}}

,

({\vec {a}}+{\vec {b}})\times {\vec {c}}={\vec {a}}\times {\vec {c}}+{\vec {b}}\times {\vec {c}}

,

(r{\vec {a}})\times {\vec {b}}=r({\vec {a}}\times {\vec {b}})={\vec {a}}\times (r{\vec {b}})

,

{\vec {a}}\times {\vec {b}}=-{\vec {b}}\times {\vec {a}}

,

{\vec {a}}\times {\vec {a}}=0

.

Für den Betrag gilt:

|{\vec {a}}\times {\vec {b}}|=|{\vec {a}}|\,|{\vec {b}}|\,\sin \varphi .\qquad (\varphi =\angle ({\vec {a}},{\vec {b}}))

Beziehung zur Determinante:

\langle {\vec {a}},{\vec {b}}\times {\vec {c}}\rangle =\det({\vec {a}},{\vec {b}},{\vec {c}}).

Jacobi-Identität:

{\vec {a}}\times ({\vec {b}}\times {\vec {c}})={\vec {b}}\times ({\vec {a}}\times {\vec {c}})-{\vec {c}}\times ({\vec {a}}\times {\vec {b}}).

Graßmann-Identität:

{\vec {a}}\times ({\vec {b}}\times {\vec {c}})={\vec {b}}\langle {\vec {a}},{\vec {c}}\rangle -{\vec {c}}\langle {\vec {a}},{\vec {b}}\rangle .

Cauchy-Binet-Identität:

\langle {\vec {a}}\times {\vec {b}},{\vec {c}}\times {\vec {d}}\rangle =\langle {\vec {a}},{\vec {c}}\rangle \langle {\vec {b}},{\vec {d}}\rangle -\langle {\vec {b}},{\vec {c}}\rangle \langle {\vec {a}},{\vec {d}}\rangle .

Lagrange-Identität:

|{\vec {a}}\times {\vec {b}}|^{2}=|{\vec {a}}|^{2}|{\vec {b}}|^{2}-\langle {\vec {a}},{\vec {b}}\rangle ^{2}.

Tensorprodukt

	Tensorprodukt
In der Ebene	${\vec {a}}\otimes {\vec {b}}={\begin{bmatrix}a_{x}\\a_{y}\end{bmatrix}}\otimes {\begin{bmatrix}b_{x}\\b_{y}\end{bmatrix}}={\begin{bmatrix}a_{x}b_{x}&a_{x}b_{y}\\a_{y}b_{x}&a_{y}b_{y}\end{bmatrix}}$
Im Raum	${\vec {a}}\otimes {\vec {b}}={\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}\otimes {\begin{bmatrix}b_{x}\\b_{y}\\b_{z}\end{bmatrix}}={\begin{bmatrix}a_{x}b_{x}&a_{x}b_{y}&a_{x}b_{z}\\a_{y}b_{x}&a_{y}b_{y}&a_{y}b_{z}\\a_{z}b_{x}&a_{z}b_{y}&a_{z}b_{z}\end{bmatrix}}$

Rechenregeln für ${\vec {a}},{\vec {b}},{\vec {c}}\in \mathbb {R} ^{n}$ und $r\in \mathbb {R}$ :

Regel	Bezeichnung
${\vec {a}}\otimes ({\vec {b}}+{\vec {c}})={\vec {a}}\otimes {\vec {b}}+{\vec {a}}\otimes {\vec {c}}$	Additivität (Distributivgesetz)
$({\vec {a}}+{\vec {b}})\otimes {\vec {c}}={\vec {a}}\otimes {\vec {c}}+{\vec {b}}\otimes {\vec {c}}$	Additivität (Distributivgesetz)
$r({\vec {a}}\otimes {\vec {b}})=(r{\vec {a}})\otimes {\vec {b}}={\vec {a}}\otimes (r{\vec {b}})$	Homogenität (Assoziativgesetz)

Lineare Abbildungen

→ Matrizen

	Endomorphismus
In der Ebene	$A{\vec {v}}={\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix}}{\begin{bmatrix}v_{x}\\v_{y}\end{bmatrix}}={\begin{bmatrix}a_{11}v_{x}+a_{12}v_{y}\\a_{21}v_{x}+a_{22}v_{y}\end{bmatrix}}$
Im Raum	$A{\vec {v}}={\begin{bmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{bmatrix}}{\begin{bmatrix}v_{x}\\v_{y}\\v_{z}\end{bmatrix}}={\begin{bmatrix}a_{11}v_{x}+a_{12}v_{y}+a_{13}v_{z}\\a_{21}v_{x}+a_{22}v_{y}+a_{23}v_{z}\\a_{31}v_{x}+a_{32}v_{y}+a_{33}v_{z}\end{bmatrix}}$

Endomorphismus	Matrix	Resultat	Inverse	Eigenwerte
Identität	$E={\begin{bmatrix}1&0\\0&1\end{bmatrix}}$	$E{\begin{bmatrix}x\\y\end{bmatrix}}={\begin{bmatrix}x\\y\end{bmatrix}}$	`E`⁻¹ = `E`	+1, +1
Skalierung	$rE={\begin{bmatrix}r&0\\0&r\end{bmatrix}}$	$rE{\begin{bmatrix}x\\y\end{bmatrix}}=r{\begin{bmatrix}x\\y\end{bmatrix}}={\begin{bmatrix}rx\\ry\end{bmatrix}}$	$(rE)^{-1}={\begin{bmatrix}1/r&0\\0&1/r\end{bmatrix}}$	`r`, `r`
Skalierung der `x`-Achse	$V_{x}={\begin{bmatrix}r&0\\0&1\end{bmatrix}}$	$V_{x}{\begin{bmatrix}x\\y\end{bmatrix}}={\begin{bmatrix}rx\\y\end{bmatrix}}$	$V_{x}^{-1}={\begin{bmatrix}1/r&0\\0&1\end{bmatrix}}$	`r`, 1
Skalierung der `y`-Achse	$V_{y}={\begin{bmatrix}1&0\\0&r\end{bmatrix}}$	$V_{y}{\begin{bmatrix}x\\y\end{bmatrix}}={\begin{bmatrix}x\\ry\end{bmatrix}}$	$V_{y}^{-1}={\begin{bmatrix}1&0\\0&1/r\end{bmatrix}}$	`r`, 1
Spiegelung an der `x`-Achse	$S_{x}={\begin{bmatrix}1&0\\0&-1\end{bmatrix}}$	$S_{x}{\begin{bmatrix}x\\y\end{bmatrix}}={\begin{bmatrix}x\\-y\end{bmatrix}}$	$S_{x}^{-1}=S_{x}$	±1
Spiegelung an der `y`-Achse	$S_{y}={\begin{bmatrix}-1&0\\0&1\end{bmatrix}}$	$S_{y}{\begin{bmatrix}x\\y\end{bmatrix}}={\begin{bmatrix}-x\\y\end{bmatrix}}$	$S_{y}^{-1}=S_{y}$	±1
Spiegelung an der Achse des Vektors `v`=(`a`, `b`)	$S({\vec {v}})={\frac {1}{a^{2}{+}b^{2}}}{\begin{bmatrix}a^{2}{-}b^{2}&2ab\\2ab&b^{2}{-}a^{2}\end{bmatrix}}$	$S({\vec {v}}){\begin{bmatrix}x\\y\end{bmatrix}}={\frac {1}{a^{2}{+}b^{2}}}{\begin{bmatrix}(a^{2}{-}b^{2})x{+}2aby\\2abx{-}(a^{2}{-}b^{2})y\end{bmatrix}}$	$S({\vec {v}})^{-1}=S({\vec {v}})$	±1
Spiegelung am Ursprung	$S_{0}={\begin{bmatrix}-1&0\\0&-1\end{bmatrix}}$	$S_{0}{\begin{bmatrix}x\\y\end{bmatrix}}={\begin{bmatrix}-x\\-y\end{bmatrix}}$	$S_{0}^{-1}=S_{0}$	−1, −1
Projektion auf die `x`-Achse	$P_{x}={\begin{bmatrix}1&0\\0&0\end{bmatrix}}$	$P_{x}{\begin{bmatrix}x\\y\end{bmatrix}}={\begin{bmatrix}x\\0\end{bmatrix}}$	nicht vorhanden	0, +1
Projektion auf die `y`-Achse	$P_{y}={\begin{bmatrix}0&0\\0&1\end{bmatrix}}$	$P_{y}{\begin{bmatrix}x\\y\end{bmatrix}}={\begin{bmatrix}0\\y\end{bmatrix}}$	nicht vorhanden	0, +1
Projektion auf die Achse des Vektors `v`=(`a`, `b`)	$P({\vec {v}})={\frac {1}{a^{2}+b^{2}}}{\begin{bmatrix}a^{2}&ab\\ab&b^{2}\end{bmatrix}}$	$P({\vec {v}}){\begin{bmatrix}x\\y\end{bmatrix}}={\frac {1}{a^{2}+b^{2}}}{\begin{bmatrix}a^{2}x+aby\\abx+b^{2}y\end{bmatrix}}$	nicht vorhanden	0, +1
Scherung an der `x`-Achse	$M_{x}={\begin{bmatrix}1&m\\0&1\end{bmatrix}}$	$M_{x}{\begin{bmatrix}x\\y\end{bmatrix}}={\begin{bmatrix}x+my\\y\end{bmatrix}}$	$M_{x}^{-1}={\begin{bmatrix}1&-m\\0&1\end{bmatrix}}$	+1, +1
Scherung an der `y`-Achse	$M_{y}={\begin{bmatrix}1&0\\m&1\end{bmatrix}}$	$M_{y}{\begin{bmatrix}x\\y\end{bmatrix}}={\begin{bmatrix}x\\mx+y\end{bmatrix}}$	$M_{y}^{-1}={\begin{bmatrix}1&0\\-m&1\end{bmatrix}}$	+1, +1
Rotation um `φ` gegen den Uhrzeigersinn	$R(\varphi )={\begin{bmatrix}\cos \varphi &-\sin \varphi \\\sin \varphi &\cos \varphi \end{bmatrix}}$	$R(\varphi ){\begin{bmatrix}x\\y\end{bmatrix}}={\begin{bmatrix}(\cos \varphi )x-(\sin \varphi )y\\(\sin \varphi )x+(\cos \varphi )y\end{bmatrix}}$	$R(\varphi )^{-1}=R(\varphi )^{T}=R(-\varphi )$	cos(`φ`)±isin(`φ`)
Rotation um `φ` im Uhrzeigersinn	$R(-\varphi )={\begin{bmatrix}\cos \varphi &\sin \varphi \\-\sin \varphi &\cos \varphi \end{bmatrix}}$	$R(-\varphi ){\begin{bmatrix}x\\y\end{bmatrix}}={\begin{bmatrix}(\cos \varphi )x+(\sin \varphi )y\\-(\sin \varphi )x+(\cos \varphi )y\end{bmatrix}}$	$R(-\varphi )^{-1}=R(-\varphi )^{T}=R(\varphi )$	cos(`φ`)±isin(`φ`)
Rotation um 90° gegen den Uhrzeigersinn	$R({\tfrac {\pi }{4}})={\begin{bmatrix}0&-1\\1&0\end{bmatrix}}$	$R({\tfrac {\pi }{4}}){\begin{bmatrix}x\\y\end{bmatrix}}={\begin{bmatrix}-y\\x\end{bmatrix}}$	$R({\tfrac {\pi }{4}})^{-1}=R(-{\tfrac {\pi }{4}})$	±i
Rotation um 90° im Uhrzeigersinn	$R(-{\tfrac {\pi }{4}})={\begin{bmatrix}0&1\\-1&0\end{bmatrix}}$	$R(-{\tfrac {\pi }{4}}){\begin{bmatrix}x\\y\end{bmatrix}}={\begin{bmatrix}y\\-x\end{bmatrix}}$	$R(-{\tfrac {\pi }{4}})^{-1}=R({\tfrac {\pi }{4}})$	±i
Entspricht der komplexen Zahl `a`+`b`i	$Z={\begin{bmatrix}a&-b\\b&a\end{bmatrix}}$	$Z{\begin{bmatrix}x\\y\end{bmatrix}}={\begin{bmatrix}ax-by\\bx+ay\end{bmatrix}}$	$Z^{-1}={\frac {1}{a^{2}+b^{2}}}{\begin{bmatrix}a&b\\-b&a\end{bmatrix}}$	`a`±`b`i
Entspricht der komplexen Zahl `r`⋅e^iφ	$Z=r{\begin{bmatrix}\cos \varphi &-\sin \varphi \\\sin \varphi &\cos \varphi \end{bmatrix}}$	$Z{\begin{bmatrix}x\\y\end{bmatrix}}=rR(\varphi ){\begin{bmatrix}x\\y\end{bmatrix}}$	$Z^{-1}={\frac {1}{r}}R(-\varphi )$	`r`cos(`φ`)±i`r`sin(`φ`)
Allgemeiner Endomorphismus	$A={\begin{bmatrix}a&b\\c&d\end{bmatrix}}$	$A{\begin{bmatrix}x\\y\end{bmatrix}}={\begin{bmatrix}ax+by\\cx+dy\end{bmatrix}}$	$A^{-1}={\frac {1}{ad-bc}}{\begin{bmatrix}d&-b\\-c&a\end{bmatrix}}$	(`a`+`d`)/2± ((`a`−`d`)²/4+`bc`)^1/2

Beliebige Basisvektoren

Skalarprodukt

→ Skalarprodukte

Bei einer Darstellung der Vektoren bezüglich belibigen Basisvektoren ${\vec {g}}_{1},{\vec {g}}_{2},{\vec {g}}_{3}$ müssen die Skalarprodukte der Basisvektoren mit in die Formel einbezogen werden. Man berechnet zunächst die Matrix:

	Metrischer Tensor
In der Ebene	$(g_{ij}):={\begin{bmatrix}\langle {\vec {g}}_{1},{\vec {g}}_{1}\rangle &\langle {\vec {g}}_{1},{\vec {g}}_{2}\rangle \\\langle {\vec {g}}_{2},{\vec {g}}_{1}\rangle &\langle {\vec {g}}_{2},{\vec {g}}_{2}\rangle \end{bmatrix}}$
Im Raum	$(g_{ij}):={\begin{bmatrix}\langle {\vec {g}}_{1},{\vec {g}}_{1}\rangle &\langle {\vec {g}}_{1},{\vec {g}}_{2}\rangle &\langle {\vec {g}}_{1},{\vec {g}}_{3}\rangle \\\langle {\vec {g}}_{2},{\vec {g}}_{1}\rangle &\langle {\vec {g}}_{2},{\vec {g}}_{2}\rangle &\langle {\vec {g}}_{2},{\vec {g}}_{3}\rangle \\\langle {\vec {g}}_{3},{\vec {g}}_{1}\rangle &\langle {\vec {g}}_{3},{\vec {g}}_{2}\rangle &\langle {\vec {g}}_{3},{\vec {g}}_{3}\rangle \end{bmatrix}}$

	Skalarprodukt
In der Ebene, ${\vec {a}}=a_{1}{\vec {g}}_{1}+a_{2}{\vec {g}}_{2}$ , ${\vec {b}}=b_{1}{\vec {g}}_{1}+b_{2}{\vec {g}}_{2}$	$\langle {\vec {a}},{\vec {b}}\rangle =g_{11}a_{1}b_{1}+g_{12}a_{1}b_{2}+g_{21}a_{2}b_{1}+g_{22}a_{2}b_{2}$
Im Raum, ${\vec {a}}=a_{1}{\vec {g}}_{1}+a_{2}{\vec {g}}_{2}+a_{3}{\vec {g}}_{3}$ , ${\vec {b}}=b_{1}{\vec {g}}_{1}+b_{2}{\vec {g}}_{2}+b_{3}{\vec {g}}_{3}$	$\langle {\vec {a}},{\vec {b}}\rangle =\sum _{i=1}^{3}\sum _{j=1}^{3}g_{ij}a_{i}b_{j}$

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.