Formelsammlung Mathematik: Ungleichungen

↑ Formelsammlung Mathematik

Bernoullische Ungleichung

(1+x)^{n}\geq 1+nx\qquad n\in \mathbb {N} ,\,x\geq -1

Beweis

Induktionsanfang: $(1+x)^{0}\geq 1$

Induktionsschluss: $(1+x)^{n+1}=(1+x)^{n}\,(1+x)\geq (1+nx)(1+x)=1+(n+1)x+nx^{2}\geq 1+(n+1)x$

Dreiecksungleichung

|z_{1}+z_{2}|\leq |z_{1}|+|z_{2}|\qquad z_{1},z_{2}\in \mathbb {C}

Beweis

$|z_{1}+z_{2}|^{2}=(z_{1}+z_{2})\left({\overline {z_{1}}}+{\overline {z_{2}}}\right)=z_{1}{\overline {z_{1}}}+z_{1}{\overline {z_{2}}}+z_{2}{\overline {z_{1}}}+z_{2}{\overline {z_{2}}}=|z_{1}|^{2}+2\,{\text{Re}}(z_{1}{\overline {z_{2}}})+|z_{2}|^{2}$ ,

dabei ist ${\text{Re}}(z_{1}{\overline {z_{2}}})\leq |z_{1}{\overline {z_{2}}}|=|z_{1}|\cdot |z_{2}|$ .

Also ist $|z_{1}+z_{2}|^{2}\leq |z_{1}|^{2}+2\cdot |z_{1}|\cdot |z_{2}|+|z_{2}|^{2}=(|z_{1}|+|z_{2}|)^{2}\,\Rightarrow \,|z_{1}+z_{2}|\leq |z_{1}|+|z_{2}|$ .

Verallgemeinerte Dreiecksungleichung

\left|\sum _{k=1}^{n}z_{k}\right|\leq \sum _{k=1}^{n}|z_{k}|\qquad z_{1},...,z_{n}\in \mathbb {C}

Beweis

Die Dreiecksungleichung $|z_{1}+z_{2}|\leq |z_{1}|+|z_{2}|$ ist der Induktionsanfang für n=2.

Induktionsschluss: $\left|\sum _{k=1}^{n+1}z_{k}\right|\leq \left|\sum _{k=1}^{n}z_{k}\right|+|z_{n+1}|\leq \sum _{k=1}^{n}|z_{k}|+|z_{n+1}|$

Cauchy-Schwarzsche-Ungleichung

Sind

{\boldsymbol {x}}=(x_{1},...,x_{n})

und

{\boldsymbol {y}}=(y_{1},...,y_{n})

reelle Vektoren, so gilt

\left(\sum _{k=1}^{n}x_{k}y_{k}\right)^{2}\leq \left(\sum _{k=1}^{n}x_{k}^{2}\right)\left(\sum _{k=1}^{n}y_{k}^{2}\right).

Kurz:

|\langle {\boldsymbol {x}},{\boldsymbol {y}}\rangle |\leq \|{\boldsymbol {x}}\|\cdot \|{\boldsymbol {y}}\|

Beweis

$0\leq \|{\boldsymbol {x}}-\lambda {\boldsymbol {y}}\|^{2}=\langle {\boldsymbol {x}}-\lambda {\boldsymbol {y}},{\boldsymbol {x}}-\lambda {\boldsymbol {y}}\rangle =\|{\boldsymbol {x}}\|^{2}-2\lambda \langle {\boldsymbol {x}},{\boldsymbol {y}}\rangle +\lambda ^{2}\|{\boldsymbol {y}}\|^{2}$

Setze $\lambda ={\frac {\langle {\boldsymbol {x}},{\boldsymbol {y}}\rangle }{\|{\boldsymbol {y}}\|^{2}}}\,:\quad 0\leq \|{\boldsymbol {x}}\|^{2}-2\,{\frac {\langle {\boldsymbol {x}},{\boldsymbol {y}}\rangle ^{2}}{\|{\boldsymbol {y}}\|^{2}}}+{\frac {\langle {\boldsymbol {x}},{\boldsymbol {y}}\rangle ^{2}}{\|{\boldsymbol {y}}\|^{2}}}\,\Rightarrow \,{\frac {\langle {\boldsymbol {x}},{\boldsymbol {y}}\rangle ^{2}}{\|{\boldsymbol {y}}\|^{2}}}\leq \|{\boldsymbol {x}}\|^{2}\,\Rightarrow \,\langle {\boldsymbol {x}},{\boldsymbol {y}}\rangle ^{2}\leq \|{\boldsymbol {x}}\|^{2}\cdot \|{\boldsymbol {y}}\|^{2}$

Ungleichungen zwischen Mittelwerten

Für

x_{1},...,x_{n}>0

, ein Gewicht

w=(w_{1},...,w_{n})

mit

\sum _{k=1}^{n}w_{k}=1

und ein

p\in \mathbb {R} \setminus \{0\}

sei

M_{w}^{p}:=\left(\sum _{k=1}^{n}w_{k}x_{k}^{p}\right)^{\frac {1}{p}}

das gewichtete Hölder-Mittel.

Es gilt

M_{w}^{0}:=\lim _{p\to 0}M_{w}^{p}=\prod _{k=1}^{n}x_{k}^{w_{k}}

und für

r<s\,

ist

M_{w}^{r}\leq M_{w}^{s}

.

Beweis

$\lim _{p\to 0}\log(M_{w}^{p})=\lim _{p\to 0}{\frac {1}{p}}\log \left(\sum _{k=1}^{n}w_{k}\,x_{k}^{p}\right)$ ${\stackrel {\text{L.H.}}{=}}\lim _{p\to 0}{\frac {\sum \limits _{k=1}^{n}w_{k}\,x_{k}^{p}\,\log x_{k}}{\sum \limits _{k=1}^{n}w_{k}\,x_{k}^{p}}}=\sum _{k=1}^{n}w_{k}\log x_{k}=\log \prod _{k=1}^{n}x_{k}^{w_{k}}$

Im Fall $0<r<s\,$ ist die Abbildung $f:\mathbb {R} ^{+}\to \mathbb {R} ^{+}\,,\,x\mapsto x^{\frac {s}{r}}$ konvex.

Nach der Jensen-Ungleichung ist daher $\left(\sum _{k=1}^{n}w_{k}\,x_{k}^{r}\right)^{\frac {s}{r}}\leq \sum _{k=1}^{n}w_{k}\,\left(x_{k}^{r}\right)^{\frac {s}{r}}\,\Rightarrow \,\left(\sum _{k=1}^{n}w_{k}\,x_{k}^{r}\right)^{\frac {1}{r}}\leq \left(\sum _{k=1}^{n}w_{k}\,x_{k}^{s}\right)^{\frac {1}{s}}$ .

Im Fall $r<s<0\,$ ist $0<-s<-r$ , woraus nach eben gezeigtem $\left(\sum _{k=1}^{n}w_{k}\,x_{k}^{-s}\right)^{\frac {1}{-s}}\leq \left(\sum _{k=1}^{n}w_{k}\,x_{k}^{-r}\right)^{\frac {1}{-r}}$ folgt.

Multipliziert man mit den Kehrwerten durch, so ist $\left(\sum _{k=1}^{n}w_{k}\,x_{k}^{-r}\right)^{\frac {1}{r}}\leq \left(\sum _{k=1}^{n}w_{k}\,x_{k}^{-s}\right)^{\frac {1}{s}}$ . Und nachdem die Ungleichung für jede

Belegung $x_{1},...,x_{n}>0\,$ gilt, ist sie auch erfüllt, wenn man jedes $x_{k}\,$ durch ${\frac {1}{x_{k}}}\,$ ersetzt. $\left(\sum _{k=1}^{n}w_{k}\,x_{k}^{r}\right)^{\frac {1}{r}}\leq \left(\sum _{k=1}^{n}w_{k}\,x_{k}^{s}\right)^{\frac {1}{s}}$

Wegen $\lim _{s\to 0}M_{w}^{s}=M_{w}^{0}=\lim _{r\to 0}M_{w}^{r}$ gilt die Ungleichung $M_{w}^{r}\leq M_{w}^{s}$ auch für $0\leq r<s$ und $r<s\leq 0$ .

Im Fall $r<0<s\,$ folgt die Ungleichung $M_{w}^{r}\leq M_{w}^{s}$ aus der Transitivität $M_{w}^{r}\leq M_{w}^{0}\leq M_{w}^{s}$ .

Insbesondere ergibt sich daraus die Ungleichungskette

\underbrace {\frac {1}{{\frac {w_{1}}{x_{1}}}+...+{\frac {w_{n}}{x_{n}}}}} _{\begin{matrix}{\text{harmonisches}}\\{\text{Mittel}}\end{matrix}}\leq \underbrace {x_{1}^{w_{1}}\cdots x_{n}^{w_{n}}} _{\begin{matrix}{\text{geometrisches}}\\{\text{Mittel}}\end{matrix}}\leq \underbrace {w_{1}x_{1}+...+w_{n}x_{n}} _{\begin{matrix}{\text{arithmetisches}}\\{\text{Mittel}}\end{matrix}}\leq \underbrace {\sqrt {w_{1}x_{1}^{2}+...+w_{n}x_{n}^{2}}} _{\begin{matrix}{\text{quadratisches}}\\{\text{Mittel}}\end{matrix}}\leq \underbrace {\sqrt[{3}]{w_{1}x_{1}^{3}+...+w_{n}x_{n}^{3}}} _{\begin{matrix}{\text{kubisches}}\\{\text{Mittel}}\end{matrix}}

.

Und daraus wiederum ergibt sich im ungewichteten/gleichgewichteten Fall

w=\left(1/n,...,1/n\right)

die Ungleichungskette

\underbrace {\frac {n}{{\frac {1}{x_{1}}}+...+{\frac {1}{x_{n}}}}} _{\begin{matrix}{\text{harmonisches}}\\{\text{Mittel}}\end{matrix}}\leq \underbrace {\sqrt[{n}]{x_{1}\cdots x_{n}}} _{\begin{matrix}{\text{geometrisches}}\\{\text{Mittel}}\end{matrix}}\leq \underbrace {\frac {x_{1}+...+x_{n}}{n}} _{\begin{matrix}{\text{arithmetisches}}\\{\text{Mittel}}\end{matrix}}\leq \underbrace {\sqrt {\frac {x_{1}^{2}+...+x_{n}^{2}}{n}}} _{\begin{matrix}{\text{quadratisches}}\\{\text{Mittel}}\end{matrix}}\leq \underbrace {\sqrt[{3}]{\frac {x_{1}^{3}+...+x_{n}^{3}}{n}}} _{\begin{matrix}{\text{kubisches}}\\{\text{Mittel}}\end{matrix}}

.

MacLaurinsche Ungleichung

Für die nichtnegativen Variablen

a_{1},...,a_{n}

sei

\sigma _{k}({\boldsymbol {a}})=\sum _{1\leq i_{1}<...<i_{k}\leq n}a_{i_{1}}\cdots a_{i_{k}}

das k-te elementarsymmetrische Polynom

und

S_{k}({\boldsymbol {a}})={\frac {\sigma _{k}({\boldsymbol {a}})}{n \choose k}}

der zugehörige elementarsymmetrische Mittelwert.

Es gilt

S_{1}({\boldsymbol {a}})\geq {\sqrt {S_{2}({\boldsymbol {a}})}}\geq {\sqrt[{3}]{S_{3}({\boldsymbol {a}})}}\geq ...\geq {\sqrt[{n}]{S_{n}({\boldsymbol {a}})}}

.

Beweis

$F(X):=(X+a_{1})\cdots (X+a_{n})$ lässt sich nach dem Satz von Vieta schreiben als $\sum _{k=0}^{n}\sigma _{k}({\boldsymbol {a}})\cdot X^{n-k}=\sum _{k=0}^{n}{n \choose k}\cdot S_{k}({\boldsymbol {a}})\cdot X^{n-k}$ .

Ist $a_{k}<a_{k+1}\,$ , so gibt es nach dem Satz von Vieta ein $b_{k}\in \,\,]a_{k},a_{k+1}[$ mit $F'(b_{k})=0$ .

Ist $a_{k}=a_{k+1}$ , so gilt für $b_{k}=a_{k}$ ebenfalls $F'(b_{k})=0$ .

Die erste Ableitung $F'\,$ lässt sich daher schreiben in der Form $F'(X)=n\cdot (X+b_{1})\cdots (X+b_{n-1})$ mit ebenfalls nichtnegativen Variablen $b_{1}\leq ...\leq b_{n-1}$ .

Zum einen ist $F'(X)={\frac {d}{dx}}\sum _{k=0}^{n}{n \choose k}\cdot S_{k}({\boldsymbol {a}})\cdot X^{n-k}=\sum _{k=0}^{n}{\frac {n!}{(n-k)!\,k!}}\cdot S_{k}({\boldsymbol {a}})\cdot (n-k)\cdot X^{n-1-k}=n\sum _{k=0}^{n-1}{n-1 \choose k}\cdot S_{k}({\boldsymbol {a}})\cdot X^{n-1-k}$ .

Zum anderen ist nach dem Satz von Vieta $F'(X)=n\sum _{k=0}^{n-1}\sigma _{k}({\boldsymbol {b}})\cdot X^{n-1-k}=n\sum _{k=0}^{n-1}{n-1 \choose k}\cdot S_{k}({\boldsymbol {b}})\cdot X^{n-1-k}$ .

Man sieht daher, dass ${\boldsymbol {a}}\,$ und ${\boldsymbol {b}}\,$ den selben symmetrischen Mittelwert besitzen, $S_{k}({\boldsymbol {a}})=S_{k}({\boldsymbol {b}})$ .

Durch Induktion folgt, dass jede weitere Ableitung von $F\,$ lauter reelle Nullstellen $\leq 0$ besitzt.

$F^{(n-m)}(X)={\frac {n!}{m!}}(X+r_{1})\cdots (X+r_{m})=\left({\frac {d}{dx}}\right)^{\!\!n-m}\sum _{k=0}^{n}{n \choose k}\cdot S_{k}({\boldsymbol {a}})\cdot X^{n-k}$

$=\sum _{k=0}^{m}{\frac {n!}{(n-k)!\,k!}}\cdot S_{k}({\boldsymbol {a}})\cdot {\frac {(n-k)!}{(m-k)!}}\cdot X^{m-k}={\frac {n!}{m!}}\cdot \sum _{k=0}^{m}{m \choose k}\cdot S_{k}({\boldsymbol {a}})\cdot X^{m-k}$ .

Nach dem Satz von Vieta lässt sich $F^{(n-m)}(X)\,$ auch in der Form ${\frac {n!}{m!}}\cdot \sum _{k=0}^{m}{m \choose k}\cdot S_{k}({\boldsymbol {r}})\cdot X^{m-k}$ schreiben.

Also stimmt bei jeder Ableitung $S_{k}({\boldsymbol {r}})\,$ mit $S_{k}({\boldsymbol {a}})\,$ überein.

Nun ist $r_{1}\cdots r_{m}=S_{m}({\boldsymbol {a}})$ und ${\widehat {r_{1}}}\,r_{2}\cdots r_{m}+r_{1}\,{\widehat {r_{2}}}\cdots r_{m}+...+r_{1}\,r_{2}\cdots {\widehat {r_{m}}}=r_{1}\cdots r_{m}\cdot \left({\frac {1}{r_{1}}}+...+{\frac {1}{r_{m}}}\right)=m\cdot S_{m-1}({\boldsymbol {a}})$ .

Nach der AM-GM Ungleichung ist ${\frac {{\widehat {r_{1}}}\,r_{2}\cdots r_{m}+r_{1}\,{\widehat {r_{2}}}\cdots r_{m}+...+r_{1}\,r_{2}\cdots {\widehat {r_{m}}}}{m}}\geq {\sqrt[{m}]{\frac {(r_{1}\,r_{2}\cdots r_{m})^{m}}{r_{1}\,r_{2}\cdots r_{m}}}}$ .

Also ist ${\frac {m\cdot S_{m-1}({\boldsymbol {a}})}{m}}\geq {\sqrt[{m}]{S_{m}({\boldsymbol {a}})^{m-1}}}\,\Rightarrow \,{\sqrt[{m-1}]{S_{m-1}({\boldsymbol {a}})}}\geq {\sqrt[{m}]{S_{m}({\boldsymbol {a}})}}$ .

Und es gilt

S_{m}({\boldsymbol {a}})^{2}\geq S_{m+1}({\boldsymbol {a}})\cdot S_{m-1}({\boldsymbol {a}})

für

m=1,...,n-1

Beweis (Newton Ungleichung)

Aus der oben verwendeten Gleichung $(X+r_{1})\cdots (X+r_{m})=\sum _{k=0}^{m}{m \choose k}\cdot S_{k}({\boldsymbol {a}})\cdot X^{m-k}$ folgt für $m=2,...,n$

$r_{1}\cdots r_{m}=S_{m}({\boldsymbol {a}})$

$r_{1}\cdots r_{m}\cdot \sum _{k=1}^{m}{\frac {1}{r_{k}}}=m\cdot S_{m-1}({\boldsymbol {a}})$

$r_{1}\cdots r_{m}\cdot \sum _{1\leq i<j\leq m}{\frac {1}{r_{i}}}\cdot {\frac {1}{r_{j}}}={\frac {m\cdot (m-1)}{2}}\cdot S_{m-2}({\boldsymbol {a}})$

$S_{m-1}({\boldsymbol {a}})^{2}\geq S_{m}({\boldsymbol {a}})\cdot S_{m-2}({\boldsymbol {a}})$ ist daher gleichbedeutend mit

$(r_{1}\cdots r_{m})^{2}\cdot {\frac {1}{m^{2}}}\cdot \left(\sum _{k=1}^{m}{\frac {1}{r_{k}}}\right)^{2}\geq (r_{1}\cdots r_{m})^{2}\cdot {\frac {2}{m\cdot (m-1)}}\sum _{1\leq i<j\leq m}{\frac {1}{r_{i}}}\cdot {\frac {1}{r_{j}}}$

$\iff (m-1)\cdot \left(\sum _{k=1}^{m}{\frac {1}{r_{k}}}\right)^{2}\geq 2m\cdot \sum _{1\leq i<j\leq m}{\frac {1}{r_{i}}}\cdot {\frac {1}{r_{j}}}$

$\iff (m-1)\cdot \left(\sum _{k=1}^{m}{\frac {1}{r_{k}}}\right)^{2}\geq m\cdot \left(\sum _{k=1}^{m}{\frac {1}{r_{k}}}\right)^{2}-m\cdot \sum _{k=1}^{m}{\frac {1}{r_{k}^{2}}}$

$\iff m\cdot \sum _{k=1}^{m}{\frac {1}{r_{k}^{2}}}\geq \left(\sum _{k=1}^{m}{\frac {1}{r_{k}}}\right)^{2}\iff {\frac {1}{m}}\sum _{k=1}^{m}{\frac {1}{r_{k}^{2}}}\geq \left({\frac {1}{m}}\sum _{k=1}^{m}{\frac {1}{r_{k}}}\right)^{2}\iff {\sqrt {{\frac {1}{m}}\sum _{k=1}^{m}{\frac {1}{r_{k}^{2}}}}}\geq {\frac {1}{m}}\sum _{k=1}^{m}{\frac {1}{r_{k}}}$ ,

was gerade die Ungleichung von quadratischen und arithmetischem Mittel ist.

Muirhead-Ungleichung

Für

n\,

-elementige Vektoren

{\boldsymbol {\nu }}\geq {\boldsymbol {0}},\,{\boldsymbol {x}}>{\boldsymbol {0}}

sei

{\mathcal {S}}\{{\boldsymbol {\nu }}\}({\boldsymbol {x}}):={\frac {1}{n!}}\sum _{\text{sym}}x_{1}^{\nu _{1}}\cdots x_{n}^{\nu _{n}}:={\frac {1}{n!}}\sum _{{\boldsymbol {\sigma }}\in S_{n}}x_{\sigma _{1}}^{\nu _{1}}\cdots x_{\sigma _{n}}^{\nu _{n}}

.

Sind

{\boldsymbol {\alpha }},{\boldsymbol {\beta }}\geq {\boldsymbol {0}}

, so gilt folgende Äquivalenz:

{\boldsymbol {\alpha }}\prec {\boldsymbol {\beta }}\iff {\mathcal {S}}\{{\boldsymbol {\alpha }}\}({\boldsymbol {x}})\leq {\mathcal {S}}\{{\boldsymbol {\beta }}\}({\boldsymbol {x}})\;\,\forall {\boldsymbol {x}}>{\boldsymbol {0}}

ohne Beweis

Logarithmischer Mittelwert

{\sqrt[{3}]{xyz}}\leq {\sqrt {{\frac {1}{2}}\,{\frac {(x-y)(y-z)(z-x)}{(x-y)\log z+(y-z)\log x+(z-x)\log y}}}}\leq {\frac {x+y+z}{3}}\qquad x>y>z>0

ohne Beweis

Abschätzung zur eulerschen Zahl

\left(1+{\frac {1}{n}}\right)^{n}<e<\left(1+{\frac {1}{n}}\right)^{n+{\frac {1}{2}}}

Beweis

Für $0<x<1\,$ ist $\log \left({\frac {1+x}{1-x}}\right)=2\sum _{k=0}^{\infty }{\frac {x^{2k+1}}{2k+1}}>2x$ .

Wegen $1+{\frac {1}{n}}={\frac {n+1}{n}}={\frac {2n+1+1}{2n+1-1}}={\frac {1+{\frac {1}{2n+1}}}{1-{\frac {1}{2n+1}}}}$

ist daher $\log \left(1+{\frac {1}{n}}\right)=\log \left({\frac {1+{\frac {1}{2n+1}}}{1-{\frac {1}{2n+1}}}}\right)>{\frac {2}{2n+1}}$

$\Rightarrow \left(n+{\frac {1}{2}}\right)\log \left(1+{\frac {1}{n}}\right)>1\,\Rightarrow \,\left(1+{\frac {1}{n}}\right)^{n+{\frac {1}{2}}}>e$ .

Monotoniebetrachtung:

Die Folge

\left(1+{\frac {1}{n}}\right)^{n}

steigt streng monoton und die Folge

\left(1+{\frac {1}{n}}\right)^{n+1}

fällt streng monoton.

Beweis

Es sei $n\geq 2\,$ eine natürliche Zahl.

$\left(1+{\frac {1}{n}}\right)^{n}>\left(1+{\frac {1}{n-1}}\right)^{n-1}\iff \left({\frac {n+1}{n}}\right)^{n}>\left({\frac {n}{n-1}}\right)^{n-1}$

$\iff \left({\frac {n^{2}-1}{n^{2}}}\right)^{n}>{\frac {n-1}{n}}\iff \left(1-{\frac {1}{n^{2}}}\right)^{n}>1-{\frac {1}{n}}$

Letzte Ungleichung gilt, weil nach der Bernoulli-Ungleichung $\left(1-{\frac {1}{n^{2}}}\right)^{n}>1+n\left({\frac {-1}{n^{2}}}\right)$ ist.

$\left(1+{\frac {1}{n-1}}\right)^{n}>\left(1+{\frac {1}{n}}\right)^{n+1}\iff \left({\frac {n}{n-1}}\right)^{n}>\left({\frac {n+1}{n}}\right)^{n+1}$

$\iff \left({\frac {n^{2}}{n^{2}-1}}\right)^{n}>{\frac {n+1}{n}}\iff \left(1+{\frac {1}{n^{2}-1}}\right)^{n}>1+{\frac {1}{n}}$

Letzte Ungleichung gilt, weil nach der Bernoulli-Ungleichung $\left(1+{\frac {1}{n^{2}-1}}\right)^{n}>1+{\frac {n}{n^{2}-1}}>1+{\frac {1}{n}}$ ist.

[Potenzen, eulersche Zahl]

(e+x)^{e-x}>(e-x)^{e+x}\qquad 0<x<e

Beweis

Definiert man $f:]0,e[\to \mathbb {R}$ durch $x\mapsto (e-x)\log(e+x)-(e+x)\log(e-x)$ ,

dann ist $\lim _{x\to 0+}f(x)=0$ und $f'(x)=\underbrace {{\frac {e-x}{e+x}}+{\frac {e+x}{e-x}}} _{>2}-\underbrace {\left(\log(e+x)+\log(e-x)\right)} _{<2}>0$ .

Daher ist $f(x)>0\,$ , also $\log \left((e+x)^{e-x}\right)>\log \left((e-x)^{e+x}\right)$ .

Napiersche-Ungleichung

{\frac {1}{a}}<{\frac {2}{a+b}}<{\frac {\log(a)-\log(b)}{a-b}}<{\frac {1}{\sqrt {ab}}}<{\frac {1}{b}}\qquad a>b>0

Beweis

Für $t>1\,$ ist $2<t+{\frac {1}{t}}$ und somit ${\frac {2}{t}}<1+{\frac {1}{t^{2}}}$ .

Für $x>1\,$ ist damit $\log(x^{2})=2\log x=2\int _{1}^{x}{\frac {1}{t}}\,dt<\int _{1}^{x}\left(1+{\frac {1}{t^{2}}}\right)\,dt=x-{\frac {1}{x}}$ und somit $\log x<{\sqrt {x}}-{\frac {1}{\sqrt {x}}}$ .

Und es ist $\log x=\sum _{k=0}^{\infty }{\frac {2}{2k+1}}\,\left({\frac {x-1}{x+1}}\right)^{2k+1}>2\,{\frac {x-1}{x+1}}$ .

Man erhält die Abschätzung $2\,{\frac {x-1}{x+1}}<\log x<{\sqrt {x}}-{\frac {1}{\sqrt {x}}}$ für $x>1\,$ .

Setze $x={\frac {a}{b}}$ dann ist $2\,{\frac {{\frac {a}{b}}-1}{{\frac {a}{b}}+1}}<\log \left({\frac {a}{b}}\right)<{\sqrt {\frac {a}{b}}}-{\sqrt {\frac {b}{a}}}$ , gleichbedeutend mit $2\,{\frac {a-b}{a+b}}<\log(a)-\log(b)<{\frac {a-b}{\sqrt {ab}}}$ .

Nesbitt-Ungleichung

{\frac {a}{b+c}}+{\frac {b}{c+a}}+{\frac {c}{a+b}}\geq {\frac {3}{2}}\qquad a,b,c>0

Beweis

Nach der AM-HM Ungleichung ist ${\frac {(b+c)+(c+a)+(a+b)}{3}}\geq {\frac {3}{{\frac {1}{b+c}}+{\frac {1}{c+a}}+{\frac {1}{a+b}}}}$ .

Somit ist $(a+b+c)\left({\frac {1}{b+c}}+{\frac {1}{c+a}}+{\frac {1}{a+b}}\right)\geq {\frac {9}{2}}$ .

Und daraus folgt ${\frac {a}{b+c}}+{\frac {b}{c+a}}+{\frac {c}{a+b}}+3\geq {\frac {9}{2}}$ .

Mahler-Ungleichung

Sind

{\boldsymbol {x}}=(x_{1},...,x_{n}),{\boldsymbol {y}}=(y_{1},...,y_{n})

Tupel positiver Zahlen, so gilt

\prod _{k=1}^{n}(x_{k}+y_{k})^{1/n}\geq \prod _{k=1}^{n}x_{k}^{1/n}+\prod _{k=1}^{n}y_{k}^{1/n}

.

Beweis

Nach der AM-GM Ungleichung ist $\prod _{k=1}^{n}\left({\frac {x_{k}}{x_{k}+y_{k}}}\right)^{1/n}\leq {\frac {1}{n}}\sum _{k=1}^{n}{\frac {x_{k}}{x_{k}+y_{k}}}$

und entsprechend $\prod _{k=1}^{n}\left({\frac {y_{k}}{x_{k}+y_{k}}}\right)^{1/n}\leq {\frac {1}{n}}\sum _{k=1}^{n}{\frac {y_{k}}{x_{k}+y_{k}}}$ .

Somit ist $\prod _{k=1}^{n}\left({\frac {x_{k}}{x_{k}+y_{k}}}\right)^{1/n}+\prod _{k=1}^{n}\left({\frac {y_{k}}{x_{k}+y_{k}}}\right)^{1/n}\leq {\frac {1}{n}}\sum _{k=1}^{n}{\frac {x_{k}+y_{k}}{x_{k}+y_{k}}}=1$ .

Multipliziert man beide Seiten mit $\prod _{k=1}^{n}(x_{k}+y_{k})^{1/n}$ durch, so ist $\prod _{k=1}^{n}x_{k}^{1/n}+\prod _{k=1}^{n}y_{k}^{1/n}\leq \prod _{k=1}^{n}(x_{k}+y_{k})^{1/n}$ .

Tschebyscheff-Summen-Ungleichung

Sind

a_{1},...,a_{n}\,

und

b_{1},...,b_{n}\,

gleichsinnig geordnete reelle Zahlen, so gilt

{\frac {1}{n}}\sum _{k=1}^{n}a_{k}\,b_{k}\geq \left({\frac {1}{n}}\sum _{k=1}^{n}a_{k}\right)\left({\frac {1}{n}}\sum _{k=1}^{n}b_{k}\right)

Beweis

Aus $(a_{k}-a_{j})(b_{k}-b_{j})\geq 0$ folgt $a_{k}b_{k}+a_{j}b_{j}\geq a_{k}b_{j}+a_{j}b_{k}$ .

Summiere nun beide Seiten nach k und j jeweils von 1 bis n:

$n\sum _{k=1}^{n}a_{k}b_{k}+n\sum _{j=1}^{n}a_{j}b_{j}\geq \sum _{k=1}^{n}a_{k}\,\sum _{j=1}^{n}b_{j}+\sum _{j=1}^{n}a_{j}\,\sum _{k=1}^{n}b_{k}$

$\Rightarrow 2n\sum _{k=1}^{n}a_{k}b_{k}\geq 2\left(\sum _{k=1}^{n}a_{k}\right)\left(\sum _{k=1}^{n}b_{k}\right)$

Tschebyscheff-Integral-Ungleichung

Sind

f,g:[0,1]\to \mathbb {R}

gleichsinnig monoton, dann gilt

\int _{0}^{1}f(x)\,g(x)\,dx\geq \int _{0}^{1}f(x)\,dx\int _{0}^{1}g(x)\,dx

.

1. Beweis

Aus ${\Big (}f(x)-f(y){\Big )}{\Big (}g(x)-g(y){\Big )}\geq 0$ folgt $f(x)\,g(x)+f(y)\,g(y)\geq f(x)\,g(y)+f(y)\,g(x)$ .

Integriere nun beide Seiten nach x und y jeweils von 0 bis 1:

$\int _{0}^{1}f(x)\,g(x)\,dx+\int _{0}^{1}f(y)\,g(y)\,dy\geq \int _{0}^{1}f(x)\,dx\,\int _{0}^{1}g(y)\,dy+\int _{0}^{1}f(y)\,dy\,\int _{0}^{1}g(x)\,dx$

$\Rightarrow 2\int _{0}^{1}f(x)\,g(x)\,dx\geq 2\int _{0}^{1}f(x)\,dx\,\int _{0}^{1}g(x)\,dx$

2. Beweis

Nach der Tschebyscheff Summen-Ungleichung ist $\sum _{k=1}^{n}f\left({\frac {k}{n}}\right){\frac {1}{n}}\;\;\sum _{k=1}^{n}g\left({\frac {k}{n}}\right){\frac {1}{n}}\leq \sum _{k=1}^{n}f\left({\frac {k}{n}}\right)g\left({\frac {k}{n}}\right){\frac {1}{n}}$ .

Für $n\to \infty \,$ gehen die Riemannschen Approximationssummen in die gewünschten Integrale über.

Anderson-Ungleichung

Sind

f_{1},...,f_{n}:[0,1]\to \mathbb {R}

nichtnegative konvexe Funktionen mit

f_{1}(0)=...=f_{n}(0)=0\,

, so gilt

\int _{0}^{1}\prod _{k=1}^{n}f_{k}(x)dx\geq {\frac {2^{n}}{n+1}}\prod _{k=1}^{n}\int _{0}^{1}f_{k}(x)dx

.

Beweis

Es sei $M\,$ die Menge der nichtnegativen konvexen Funktionen $f:[0,1]\to \mathbb {R}$ mit $f(0)=0\,$ .

$(1)\,$ Jede Funktion $f\in M$ wächst monoton, denn gäbe es $0\leq x_{1}<x_{2}\leq 1$ , so dass $f(x_{1})>f(x_{2})\,$ ist,

so würde der Punkt ${\big (}x_{1},f(x_{1}){\big )}$ überhalb der Sekante $\ell (x)={\frac {f(x_{2})}{x_{2}}}\cdot x$ liegen.

$(2)\,$ $M\,$ ist abgeschlossen bezüglich der Multiplikation, das heißt aus $f,g\in M$ folgt $f\cdot g\in M$ .

Da $f\,$ und $g\,$ beide monoton wachsen, ist $[f(x)-f(y)]\,[g(x)-g(y)]\geq 0$ ,

woraus $f(x)g(x)+f(y)g(y)\geq f(x)g(y)+f(y)g(x)$ folgt.

Für $\alpha ,\beta \geq 0$ mit $\alpha +\beta =1\,$ ist dann $(fg)(\alpha x+\beta y)=f(\alpha x+\beta y)\,g(\alpha x+\beta y)$

$\leq [\alpha f(x)+\beta f(y)]\,[\alpha g(x)+\beta g(y)]$ , nachdem $f\,$ und $g\,$ konvex sind.

Und das ist $\alpha ^{2}f(x)g(x)+\alpha \beta [f(x)g(y)+f(y)g(x)]+\beta ^{2}f(y)g(y)\,$

$\leq \alpha ^{2}f(x)g(x)+\alpha \beta [f(x)g(x)+f(y)g(y)]+\beta ^{2}f(y)g(y)$

$=\underbrace {(\alpha ^{2}+\alpha \beta )} _{=\alpha }f(x)g(x)+\underbrace {(\alpha \beta +\beta ^{2})} _{=\beta }f(y)g(y)=\alpha \,(fg)(x)+\beta \,(fg)(y)$ .

$(3)\,$ Definiert man ${\widehat {f}}(x)=2x\int _{0}^{1}f(t)\,dt$ , dann gilt die Implikation $f\in M\Rightarrow {\widehat {f}}\in M$ .

$(4)\,$ Für alle $f,g\in M$ gilt die Ungleichung $\int _{0}^{1}g(x)\,f(x)\,dx\geq \int _{0}^{1}g(x)\,{\widehat {f}}(x)\,dx$ .

Die Flächen $\int _{0}^{1}{\widehat {f}}(x)\,dx$ und $\int _{0}^{1}f(x)\,dx$ sind gleich.

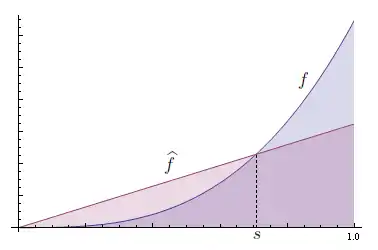
Es gibt einen Wert $0<s<1\,$ , so dass $f(x)\leq {\widehat {f}}(x)$ für alle $x\leq s\,$ ist und $f(x)\geq {\widehat {f}}(x)$ für alle $x\geq s\,$ ist.

Also ist $\int _{0}^{s}{\widehat {f}}(x)\,dx+\int _{s}^{1}{\widehat {f}}(x)\,dx=\int _{0}^{s}f(x)\,dx+\int _{s}^{1}f(x)\,dx$

$\Rightarrow \int _{0}^{s}\left({\widehat {f}}(x)-f(x)\right)dx=\int _{s}^{1}\left(f(x)-{\widehat {f}}(x)\right)dx$

Nachdem $g\,$ monoton wächst, ist $\int _{0}^{s}g(x)\left({\widehat {f}}(x)-f(x)\right)dx$

$\leq g(s)\int _{0}^{s}\left({\widehat {f}}(x)-f(x)\right)dx=g(s)\int _{s}^{1}\left(f(x)-{\widehat {f}}(x)\right)dx$

$\leq \int _{s}^{1}g(x)\left(f(x)-{\widehat {f}}(x)\right)dx=-\int _{s}^{1}g(x)\left({\widehat {f}}(x)-f(x)\right)dx$ .

Daher ist $\int _{0}^{1}g(x)\left({\widehat {f}}(x)-f(x)\right)dx\leq 0\Rightarrow \int _{0}^{1}g(x)\,{\widehat {f}}(x)\,dx\leq \int _{0}^{1}g(x)\,f(x)\,dx$ .

Für $f_{1},...,f_{n}\in M$ gilt dann

$\int _{0}^{1}f_{1}(x)\cdots f_{n}(x)\,dx\geq \int _{0}^{1}{\widehat {f}}_{1}(x)\cdots {\widehat {f}}_{n}(x)\,dx=\int _{0}^{1}2x\int _{0}^{1}f_{1}(t)\,dt\cdots 2x\int _{0}^{1}f_{n}(t)\,dt\,\,dx$

$=\int _{0}^{1}2^{n}x^{n}\,dx\int _{0}^{1}f_{1}(t)\,dt\cdots \int _{0}^{1}f_{n}(t)\,dt={\frac {2^{n}}{n+1}}\prod _{i=1}^{n}\int _{0}^{1}f_{i}(x)\,dx$ .

Abschätzung zu log(1+x), cos(x), sin(x)

\forall x\geq 0

ist

\sum _{k=0}^{n}\left[{\frac {x^{k+1}}{k+1}},{\frac {x^{2k}}{(2k)!}},{\frac {x^{2k+1}}{(2k+1)!}}\right]

\left\{{\begin{matrix}>&,&n=2m\quad \;\;\,\\<&,&n=2m+1\end{matrix}}\right\}\;{\Big [}\log(1+x),\cos(x),\sin(x){\Big ]}

ohne Beweis

[Mit der Stirling-Formel verwandte Formel]

(n-1)!<{\frac {n^{n}}{e^{n}}}\,e<n!\qquad n\in \mathbb {Z} ^{>1}

1. Beweis

${\frac {n^{n}}{n!}}=\prod _{k=1}^{n-1}\left(1+{\frac {1}{k}}\right)^{k}<e^{n-1}<\prod _{k=1}^{n-1}\left(1+{\frac {1}{k}}\right)^{k+1}={\frac {n^{n}}{(n-1)!}}$

2. Beweis

Da der natürliche Logarithmus streng monoton wächst ist $\log(k)<\int _{k}^{k+1}\log(x)\,dx<\log(k+1)$ .

Summiert man nach $k\,$ von $1\,$ bis $n-1\,$ , so ist $\log(n-1)!<\int _{1}^{n}\log(x)\,dx<\log n!$ .

Dabei ist $\int _{1}^{n}\log(x)\,dx=\left[x\,\log(x)-x\right]_{1}^{n}=n\,\log(n)-n+1=\log \left({\frac {n^{n}}{e^{n}}}\,e\right)$ .

Also ist $(n-1)!<{\frac {n^{n}}{e^{n}}}\,e<n!$ .

[Ungleichungen mit der Gammafunktion]

\Gamma {\Big (}x\alpha +(1-x)\beta {\Big )}\leq \Gamma (\alpha )^{x}\,\Gamma (\beta )^{1-x}\qquad \alpha ,\beta >0\qquad 0\leq x\leq 1

Beweis

$\Gamma {\Big (}x\alpha +(1-x)\beta {\Big )}=\int _{0}^{\infty }t^{x\alpha +(1-x)\beta -1}\,e^{-t}\,dt=\int _{0}^{\infty }t^{(\alpha -1)x+(\beta -1)(1-x)}\,e^{-t}\,dt$

$=\int _{0}^{\infty }(t^{\alpha -1}\,e^{-t})^{x}\,(t^{\beta -1}\,e^{-t})^{1-x}dt$ ist nach der Hölderungleichung

$\leq \left(\int _{0}^{\infty }t^{\alpha -1}\,e^{-t}\,dt\right)^{x}\,\left(\int _{0}^{\infty }t^{\beta -1}\,e^{-t}\,dt\right)^{1-x}=\Gamma (\alpha )^{x}\,\Gamma (\beta )^{1-x}$ .

n!\,(n+x)^{x-1}\leq \Gamma (n+x)\leq \Gamma (n)\,n^{x}\qquad 0\leq x\leq 1\qquad 1\leq n

Beweis

In der Ungleichung $\Gamma {\Big (}x\alpha +(1-x)\beta {\Big )}\leq \Gamma (\alpha )^{x}\,\Gamma (\beta )^{1-x}$ für $\alpha ,\beta >0\,$ und $0\leq x\leq 1$

setze $\alpha =n+1\,$ und $\beta =n\,$ , so ist $\Gamma (n+x)\leq \Gamma (n+1)^{x}\,\Gamma (n)^{1-x}=\Gamma (n)\,n^{x}$ .

Setzt man hingegen $\alpha =n+x\,$ und $\beta =n+1+x\,$ , so ist

$\Gamma (n+1)\leq \Gamma (n+x)^{x}\,\Gamma (n+1+x)^{1-x}=\Gamma (n+x)\,(n+x)^{1-x}$ .

Und somit ist $n!\,(n+x)^{x-1}\leq \Gamma (n+x)$ .

Gautschis Ungleichung

x^{1-s}<{\frac {\Gamma (x+1)}{\Gamma (x+s)}}<(x+1)^{1-s}\qquad 0<s<1

ohne Beweis

Carlson-Ungleichung

Ist

a_{1},a_{2},a_{3},...

eine Folge nichtnegativer Zahlen, wobei nicht alle Folgeglieder verschwinden, so gilt

\left(\sum _{k=1}^{\infty }a_{k}\right)^{4}<\pi ^{2}\,\sum _{k=1}^{\infty }a_{k}^{2}\cdot \sum _{k=1}^{\infty }k^{2}a_{k}^{2}

Hardys erster Beweis der Carlson-Ungleichung

Sei $\alpha ,\beta >0$ und setze $S=\sum _{k=1}^{\infty }a_{k}^{2}$ und $T=\sum _{k=1}^{\infty }k^{2}a_{k}^{2}$ .

$\left(\sum _{k=1}^{\infty }a_{k}\right)^{2}=\left(\sum _{k=1}^{\infty }a_{k}\cdot {\sqrt {\alpha +\beta k^{2}}}\cdot {\frac {1}{\sqrt {\alpha +\beta k^{2}}}}\right)^{2}$ ist nach Cauchy-Schwarzscher-Ungleichung

$\leq \sum _{k=1}^{\infty }a_{k}^{2}\cdot (\alpha +\beta k^{2})\cdot \sum _{k=1}^{\infty }{\frac {1}{\alpha +\beta k^{2}}}=(\alpha \cdot S+\beta \cdot T)\cdot \sum _{k=1}^{\infty }{\frac {1}{\alpha +\beta k^{2}}}<(\alpha \cdot S+\beta \cdot T)\cdot \int _{0}^{\infty }{\frac {dx}{\alpha +\beta x^{2}}}$

$=(\alpha \cdot S+\beta \cdot T)\cdot {\frac {\pi }{2}}\,{\frac {1}{\sqrt {\alpha \beta }}}={\frac {\pi }{2}}\left({\sqrt {\frac {\alpha }{\beta }}}\cdot S+{\sqrt {\frac {\beta }{\alpha }}}\cdot T\right)$ .

Setzt man $\alpha =T\,$ und $\beta =S\,$ , so ist $\left(\sum _{k=1}^{\infty }a_{k}\right)^{2}<{\frac {\pi }{2}}\left({\sqrt {ST}}+{\sqrt {ST}}\,\right)=\pi {\sqrt {ST}}$ .

Durchquadrieren liefert die Behauptung.

Hardys zweiter Beweis der Carlson-Ungleichung

Betrachte die Fourierreihe $f(x)=\sum _{k=1}^{\infty }a_{k}\,\cos kx$ mit deren Ableitung $f'(x)=\sum _{k=1}^{\infty }-ka_{k}\,\sin kx$ .

Nach der Parsevalschen Gleichung ist ${\frac {2}{\pi }}\int _{0}^{\pi }f^{2}(x)\,dx=\sum _{k=1}^{\infty }a_{k}^{2}=:S$ und ${\frac {2}{\pi }}\int _{0}^{\pi }f'^{2}(x)\,dx=\sum _{k=1}^{\infty }k^{2}a_{k}^{2}=:T$ .

Wegen $\int _{0}^{\pi }f(x)\,dx=\sum _{k=1}^{\infty }a_{k}\left[{\frac {\sin kx}{k}}\right]_{0}^{\pi }=0$ , gibt es ein $0<\xi <\pi$ , so dass $f(\xi )=0$ ist.

Also ist $\left(\sum _{k=1}^{\infty }a_{k}\right)^{2}=f^{2}(0)=f^{2}(0)-f^{2}(\xi )=2\int _{\xi }^{0}f(x)\,f'(x)\,dx$ , und das ist nach Cauchy-Schwarzscher-Ungleichung

$<2\cdot {\sqrt {\int _{0}^{\pi }f^{2}(x)\,dx}}\cdot {\sqrt {\int _{0}^{\pi }f'^{2}(x)\,dx}}=2\cdot {\sqrt {{\frac {\pi }{2}}\,S}}\cdot {\sqrt {{\frac {\pi }{2}}\,T}}=\pi \,{\sqrt {ST}}$ .

Durchquadrieren liefert die Behauptung.

Hilbertsche Ungleichung

Sind

(a_{n}),(b_{m})

zwei nichtnegative Zahlenfolgen, bei denen nicht alle Folgeglieder verschwinden und sind

p,q\,

zwei Zahlen,

so dass

1<p,q<\infty

und

{\frac {1}{p}}+{\frac {1}{q}}=1

ist, dann gilt

\sum _{n=1}^{\infty }\sum _{m=1}^{\infty }{\frac {a_{n}\,b_{m}}{n+m}}<{\frac {\pi }{\sin {\frac {\pi }{p}}}}\cdot \left(\sum _{n=1}^{\infty }a_{n}^{p}\right)^{\frac {1}{p}}\cdot \left(\sum _{m=1}^{\infty }b_{m}^{q}\right)^{\frac {1}{q}}

.

Beweis

Für ein $0<\alpha <1$ ist die Riemannsche Approximationssumme $\sum _{m=1}^{\infty }{\frac {1}{\left(1+{\frac {m}{n}}\right)\cdot \left({\frac {m}{n}}\right)^{\alpha }}}\,{\frac {1}{n}}$

kleiner als das Integral $\int _{0}^{\infty }{\frac {1}{(1+x)\,x^{\alpha }}}\,dx={\frac {\pi }{\sin \pi \alpha }}$ , weil der Integrand $f(x)={\frac {1}{(1+x)\,x^{\alpha }}}$ streng monoton fällt.

Nun ist $\sum _{n,m=1}^{\infty }{\frac {a_{n}\,b_{m}}{n+m}}=\sum _{n,m=1}^{\infty }{\frac {a_{n}}{(n+m)^{\frac {1}{p}}\,\left({\frac {m}{n}}\right)^{\frac {1}{pq}}}}\cdot {\frac {b_{m}}{(n+m)^{\frac {1}{q}}\,\left({\frac {n}{m}}\right)^{\frac {1}{pq}}}}$ nach der Hölderschen Ungleichung

$<\left(\sum _{n,m=1}^{\infty }{\frac {a_{n}^{p}}{(n+m)\,\left({\frac {m}{n}}\right)^{\frac {1}{q}}}}\right)^{\frac {1}{p}}\cdot \left(\sum _{n,m=1}^{\infty }{\frac {b_{m}^{q}}{(n+m)\,\left({\frac {n}{m}}\right)^{\frac {1}{p}}}}\right)^{\frac {1}{q}}$

$=\left(\sum _{n=1}^{\infty }a_{n}^{p}\cdot \sum _{m=1}^{\infty }{\frac {1}{(n+m)\,\left({\frac {m}{n}}\right)^{\frac {1}{q}}}}\right)^{\frac {1}{p}}\cdot \left(\sum _{m=1}^{\infty }b_{m}^{q}\cdot \sum _{n=1}^{\infty }{\frac {1}{(n+m)\,\left({\frac {n}{m}}\right)^{\frac {1}{p}}}}\right)^{\frac {1}{q}}$

$<\left(\sum _{n=1}^{\infty }a_{n}^{p}\right)^{\frac {1}{p}}\cdot \left({\frac {\pi }{\sin {\frac {\pi }{q}}}}\right)^{\frac {1}{p}}\cdot \left(\sum _{m=1}^{\infty }b_{m}^{q}\right)^{\frac {1}{q}}\cdot \left({\frac {\pi }{\sin {\frac {\pi }{p}}}}\right)^{\frac {1}{q}}={\frac {\pi }{\sin {\frac {\pi }{p}}}}\cdot \left(\sum _{n=1}^{\infty }a_{n}^{p}\right)^{\frac {1}{p}}\cdot \left(\sum _{m=1}^{\infty }b_{m}^{q}\right)^{\frac {1}{q}}$ .

Hilbertsche Ungleichung für Integrale

Sind

f,g:\mathbb {R} _{\geq 0}\to \mathbb {R} _{\geq 0}

zwei stetige Funktionen ungleich der Nullfunktion, so gilt

\int _{0}^{\infty }\int _{0}^{\infty }{\frac {f(x)\,g(y)}{x+y}}\,dx\,dy<{\frac {\pi }{\sin {\frac {\pi }{p}}}}\cdot \left(\int _{0}^{\infty }[f(x)]^{p}\,dx\right)^{\frac {1}{p}}\cdot \left(\int _{0}^{\infty }[g(y)]^{q}\,dy\right)^{\frac {1}{q}}

.

ohne Beweis

Hardy-Ungleichung für Integrale

Ist

f:\mathbb {R} _{\geq 0}\to \mathbb {R} _{\geq 0}

eine integrierbare Funktion und ist

p>1

, so gilt

\int _{0}^{\infty }\left({\frac {1}{x}}\int _{0}^{x}f(t)\,dt\right)^{p}dx\leq \left({\frac {p}{p-1}}\right)^{p}\cdot \int _{0}^{\infty }[f(x)]^{p}\,dx

Beweis

Setze $F(x):=\int _{0}^{x}f(t)\,dt$ .

Nach der Substitution $t=x\cdot u^{\frac {p}{r}}\,\Rightarrow \,dt=x\cdot {\frac {p}{r}}\cdot u^{{\frac {p}{r}}-1}\,du$ ist

$F(x)=x\cdot {\frac {p}{r}}\cdot \int _{0}^{1}f\left(x\cdot u^{\frac {p}{r}}\right)\cdot u^{{\frac {p}{r}}-1}\,du\Rightarrow [F(x)]^{p}=x^{p}\cdot \left({\frac {p}{r}}\right)^{p}\cdot \left(\int _{0}^{1}f\left(x\cdot u^{\frac {p}{r}}\right)\cdot u^{{\frac {p}{r}}-1}\,du\right)^{p}$ .

Da die Abbildung $u\mapsto u^{p}$ konvex ist, gilt nach der Jensen-Ungleichung

$\left(\int _{0}^{1}f\left(x\cdot u^{\frac {p}{r}}\right)\cdot u^{{\frac {p}{r}}-1}\,du\right)^{p}\leq \int _{0}^{1}\left[f\left(x\cdot u^{\frac {p}{r}}\right)\right]^{p}\cdot u^{p\cdot \left({\frac {p}{r}}-1\right)}\cdot du$ .

Mache beim letzten Term die Substitution $t=x\cdot u^{\frac {p}{r}}$ rückgängig. $\left(u^{p}={\frac {t^{r}}{x^{r}}}\,\Rightarrow \,u={\frac {t^{\frac {r}{p}}}{x^{\frac {r}{p}}}}\,\Rightarrow \,du={\frac {r}{p}}\cdot {\frac {t^{{\frac {r}{p}}-1}}{x^{\frac {r}{p}}}}\,dt\right)$

Der letzte Term ist dann $\int _{0}^{x}[f(t)]^{p}\cdot {\frac {t^{p-r}}{x^{p-r}}}\cdot {\frac {r}{p}}\cdot {\frac {t^{{\frac {r}{p}}-1}}{x^{\frac {r}{p}}}}\,dt={\frac {x^{r-{\frac {r}{p}}}}{x^{p}}}\cdot {\frac {r}{p}}\cdot \int _{0}^{x}\left[f(t)\right]^{p}\cdot t^{p-r+{\frac {r}{p}}-1}\,dt$ .

Also ist $[F(x)]^{p}\leq x^{r-{\frac {r}{p}}}\cdot \left({\frac {p}{r}}\right)^{p-1}\cdot \int _{0}^{x}[f(t)]^{p}\cdot t^{p-r+{\frac {r}{p}}-1}\,dt$ .

Und damit ist $\int _{0}^{\infty }[F(x)]^{p}\cdot x^{-r-1}\,dx\leq \int _{0}^{\infty }x^{r-{\frac {r}{p}}}\cdot \left({\frac {p}{r}}\right)^{p-1}\cdot \int _{0}^{x}[f(t)]^{p}\cdot t^{p-r+{\frac {r}{p}}-1}\,dt\cdot x^{-r-1}\,dx$

$=\left({\frac {p}{r}}\right)^{p-1}\cdot \int _{0}^{\infty }\int _{0}^{x}[f(t)]^{p}\cdot t^{p-r+{\frac {r}{p}}-1}\cdot x^{-{\frac {r}{p}}-1}\,dt\,dx=\left({\frac {p}{r}}\right)^{p-1}\cdot \int _{0}^{\infty }[f(t)]^{p}\cdot t^{p-r+{\frac {r}{p}}-1}\cdot \int _{t}^{\infty }x^{-{\frac {r}{p}}-1}\,dx\cdot dt$

$=\left({\frac {p}{r}}\right)^{p}\cdot \int _{0}^{\infty }[f(t)]^{p}\cdot t^{p-r-1}\,dt$ .

Setzt man $r=p-1$ , so ist $\int _{0}^{\infty }\left({\frac {F(x)}{x}}\right)^{p}dx\leq \left({\frac {p}{p-1}}\right)^{p}\cdot \int _{0}^{\infty }[f(t)]^{p}\,dt$ .

Hardy-Ungleichung für Reihen

Ist

(a_{n})

eine Folge nichtnegativer reeller Zahlen und ist

p>1\,

, so gilt

\sum _{n=1}^{\infty }\left({\frac {1}{n}}\sum _{k=1}^{n}a_{k}\right)^{p}\leq \left({\frac {p}{p-1}}\right)^{p}\cdot \sum _{k=1}^{\infty }a_{k}^{p}

Beweis

Gibbssche Ungleichung

Sind

{\boldsymbol {p}}=(p_{1},...,p_{n})

und

{\boldsymbol {q}}=(q_{1},...,q_{n})

diskrete Wahrscheinlichkeitsverteilungen

mit

p_{1}\geq ...\geq p_{n}>0\,\,,\,\,q_{1}\geq ...\geq q_{n}>0

und

\sum _{k=1}^{n}p_{k}=\sum _{k=1}^{n}q_{k}=1

, so gilt

-\sum _{k=1}^{n}p_{k}\log(p_{k})\leq -\sum _{k=1}^{n}p_{k}\log(q_{k})

, wobei Gleichheit nur im Fall

{\boldsymbol {p}}={\boldsymbol {q}}

auftritt.

Beweis

$\log \left({\frac {q_{k}}{p_{k}}}\right)\leq {\frac {q_{k}}{p_{k}}}-1$

$\Rightarrow \,p_{k}\cdot \log \left({\frac {q_{k}}{p_{k}}}\right)\leq q_{k}-p_{k}$

$\Rightarrow \,\sum _{k=1}^{n}p_{k}\cdot \log \left({\frac {q_{k}}{p_{k}}}\right)\leq \sum _{k=1}^{n}q_{k}-\sum _{k=1}^{n}p_{k}=0$

$\Rightarrow \,\sum _{k=1}^{n}p_{k}\log(q_{k})\leq \sum _{k=1}^{n}p_{k}\log(p_{k})$

$\Rightarrow \,-\sum _{k=1}^{n}p_{k}\log(p_{k})\leq -\sum _{k=1}^{n}p_{k}\log(q_{k})$

Diskrete jensensche Ungleichung

Ist

f:[a,b]\to \mathbb {R}

konvex und sind

\lambda _{1},...,\lambda _{n}

nichtnegative Zahlen mit

\sum _{k=1}^{n}\lambda _{k}=1

,

dann gilt für beliebige

x_{1},...,x_{n}\in [a,b]

die Ungleichung

f\left(\sum _{k=1}^{n}\lambda _{k}\,x_{k}\right)\leq \sum _{k=1}^{n}\lambda _{k}\,f(x_{k})

.

Beweis

Im Fall $n=2$ gilt für eine konvexe Funktion $f\,$ die Ungleichung $f(\lambda _{1}x_{1}+\lambda _{2}x_{2})\leq \lambda _{1}f(x_{1})+\lambda _{2}f(x_{2})$ per Definition.

Induktionsschritt:

Aus $\sum _{k=1}^{n+1}\lambda _{k}=1$ folgt $\sum _{k=1}^{n}{\frac {\lambda _{k}}{1-\lambda _{n+1}}}=1$ .

$f\left(\sum _{k=1}^{n+1}\lambda _{k}x_{k}\right)=f\left((1-\lambda _{n+1})\cdot \sum _{k=1}^{n}{\frac {\lambda _{k}}{1-\lambda _{n+1}}}\cdot x_{k}+\lambda _{n+1}\cdot x_{n+1}\right)$

$\leq (1-\lambda _{n+1})\cdot f\left(\sum _{k=1}^{n}{\frac {\lambda _{k}}{1-\lambda _{n+1}}}\cdot x_{k}\right)+\lambda _{n+1}\cdot f(x_{n+1})$

$\leq (1-\lambda _{n+1})\cdot \sum _{k=1}^{n}{\frac {\lambda _{k}}{1-\lambda _{n+1}}}\cdot f(x_{k})+\lambda _{n+1}\cdot f(x_{n+1})=\sum _{k=1}^{n+1}\lambda _{k}\,f(x_{k})$

Jensensche Ungleichung für Integrale

Ist

g:[a,b]\to \mathbb {R}

eine integrierbare Funktion, so dass

f\,

im Bild von

g\,

konvex ist,

dann gilt

f\left({\frac {1}{b-a}}\int _{a}^{b}g(x)\,dx\right)\leq {\frac {1}{b-a}}\int _{a}^{b}f\left(g(x)\right)dx

Beweis

Sei zunächst ${\displaystyle \varphi$ eine integrierbare Funktion, so dass $f\,$ im Bild von $\varphi \,$ konvex ist.

In der diskreten Jensen-Ungleichung $f\left(\sum _{k=1}^{n}\lambda _{k}\,x_{k}\right)\leq \sum _{k=1}^{n}\lambda _{k}\,f(x_{k})$ setze $\lambda _{k}={\frac {1}{n}}$ und $x_{k}=\varphi \left({\frac {k}{n}}\right)$ .

$f\left(\sum _{k=1}^{n}\varphi \left({\frac {k}{n}}\right)\cdot {\frac {1}{n}}\right)\leq \sum _{k=1}^{n}f\left(\varphi \left({\frac {k}{n}}\right)\right)\cdot {\frac {1}{n}}$

Für $n\to \infty$ ergibt sich $f\left(\int _{0}^{1}\varphi (u)\,du\right)\leq \int _{0}^{1}f(\varphi (u))\,du$ .

Nach der Substitution $u={\frac {x-a}{b-a}}\,\Rightarrow \,du={\frac {dx}{b-a}}$ ist

$f\left(\int _{a}^{b}\varphi \left({\frac {x-a}{b-a}}\right){\frac {dx}{b-a}}\right)\leq \int _{a}^{b}f\left(\varphi \left({\frac {x-a}{b-a}}\right)\right){\frac {dx}{b-a}}$

Setze $g(x):=\varphi \left({\frac {x-a}{b-a}}\right)$ , dann ist $f\left({\frac {1}{b-a}}\int _{a}^{b}g(x)\,dx\right)\leq {\frac {1}{b-a}}\int _{a}^{b}f(g(x))\,dx$ .

Hlawka-Ungleichung

\|\mathbf {x} +\mathbf {y} \|+\|\mathbf {y} +\mathbf {z} \|+\|\mathbf {z} +\mathbf {x} \|\leq \|\mathbf {x} \|+\|\mathbf {y} \|+\|\mathbf {z} \|+\|\mathbf {x} +\mathbf {y} +\mathbf {z} \|\qquad \mathbf {x} ,\mathbf {y} ,\mathbf {z} \in \mathbb {C} ^{n}

ohne Beweis

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.