| ↑ Formelsammlung Mathematik |
Exponentialreihe
Logarithmus
Winkelfunktionen
Sinus
Kosinus
Tangens
Ersetzt man in der Reihenentwicklung
Die Variable durch ,
so ist .
Kotangens
Ersetzt man in der Reihenentwicklung für
durch
so ist .
Sekans
Kosekans
Ersetzt man in der Reihenentwicklung
die Variable durch , so ist .
Hyperbelfunktionen
Sinus Hyperbolicus
Kosinus Hyperbolicus
Tangens Hyperbolicus
Aus der Reihenentwicklung für
und der Identität folgt dass für
sein muss.
Kotangens Hyperbolicus
Für ist .
Somit ist . Und das ist .
Ersetzt man durch so erhält man die Formel für .
Sekans Hyperbolicus
Kosekans Hyperboliucs
Aus der Reihenentwicklung für
und der Identität folgt dass
sein muss.
Arkusfunktionen
Arkussinus
Ausdruck mit Arkussinus
Aus folgt und daraus
.
Die analytische Funktion ist ungerade und besitzt daher eine Taylorreihenentwicklung der Form .
Durch die Ableitung ergibt sich die Differenzialgleichung .
Durch das Einsetzen der Reihenentwicklung von in die Differenzialgleichung soll nun eine Rekursionsformel für die Koeffizienten gefunden werden.
Es ist und somit .
Und aus ergibt sich durch Indexverschiebung .
Also ist . Und dies soll mit übereinstimmen.
Durch Koeffizientenvergleich ergibt sich und die Rekursionsformel , gleichbedeutend mit .
Demzufolge lässt sich schreiben als Teleskopprodukt . Und das ist . Also ist .
Potenzen des Arkussinus
Integriert man die Formel auf beiden Seiten, so ist .
Aus der Formel
für und
folgt unmittelbar
Lässt man gehen, so ist
Dabei ist .
Also ist .
Ersetze durch um die gesuchte Reihenentwicklung zu erhalten.
Setzt man , so ist .
Mache den Ansatz , und differenziere beide Seiten zweimal:
Es muss also und sein.
Somit ist .
Also ist .
Setzt man , so ist .
Es ist ,
wobei ist und somit gilt.
Mache den Ansatz , mit , und differenziere beide Seiten zweimal:
.
Also ist .
Setzt man , so ist .
Es ist ,
wobei und somit ist.
Mache den Ansatz , mit , und differenziere beide Seiten zweimal:
.
Also ist .
Arkuskosinus
Arkustangens
Areafunktionen
Areasinus Hyperbolicus
Potenzen des Areasinus Hypoerbolicus
Areatangens Hyperbolicus
Spezielle Funktionen
Zeta-Funktion
Man erhält die Gleichung ,
welche insbesondere ein Spezialfall der Eulerschen Summenformel ist.
Wende auf an, ,
setze , ,
und lasse gehen, .
Betrachte nun nur für und lasse erst gehen, ,
wende darauf an, ,
und lasse gehen, .
Vergleicht man mit , so erkennt man, dass
sein muss.
Die Reihenentwicklung von im Punkt lautet also .
Gamma-Funktion
Digamma-Funktion
Bessel-Funktionen
Lambert W-Funktion
Die holomorphe Funktion
bildet null auf null ab und ist wegen im Punkt lokal biholomorph.
Es gibt also Umgebungen und , so dass biholomorph ist.
Die Koeffizienten der Umkehrfunktion
erhält man mit der Lagrange'schen Inversonsformel .
Dabei ist , somit
und somit ist .
[Reihe mit Bessel-Funktion]
Da für verschwindet, kann man auch alle ganzen Zahlen durchlaufen lassen.
Anschließend vertauscht man die Summationsreihenfolge.
Bei der Laurentreihenentwicklung
lassen sich die Koeffizienten mit der Formel berechnen.
Hierbei ist eine geschlossene Kurve, die den Ursprung einmal gegen den Urzeigersinn umläuft.
Die Funktion ist für auf ganz meromorph; sie besitzt also nicht die Unstetigkeitsachse .
Bei der Hankelschen Integraldarstellung der Besselfunktion,
,
kann man daher für die Kurve als bei geschlossen betrachten. Also ist .
Ausdrücke mit Winkelfunktionen
cos(αx)/sin(απ)
sin(αx)/sin(απ)
Es sei und das Quadrat mit den Eckpunkten .
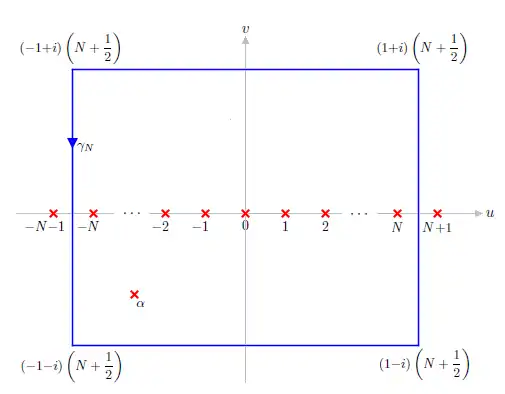
Ist so gilt und wegen ist
für .
Daher fällt für exponentiell ab.
Somit gilt . Die Summe aller Residuen von muss daher verschwinden.
ist und .
Also ist .
Ein Vergleich der Real- und Imaginärteile auf beiden Seiten liefert die Behauptung.
cot(πz)
csc(πz)
tan(πz)
sec(πz)
sin(α arcsin(z))
Ausdrücke mit Wurzeln
9.1
.
mit
9.2
.
mit
9.3
Ausdrücke mit Hyperbelfunktionen
10.1
Die Funktion hat bei einen Pol dritter Ordnung.
Die Laurentreihen-Entwicklung von um hat den Hauptteil .
Alle weiteren Polstellen von sind einfache Polstellen bei
Setze
, hierbei ist
Also ist
.
Die Funktion ist holomorph auf ganz .
Wegen für , ist eine beschränkte ganze Funktion, und damit konstant. (Satz von Liouville)
Die Konstante verschwindet, da ist. Also ist .
10.2
Betrachte folgende Formel:
Ersetze durch :
Zähle beide Gleichungen zusammen:
Multipliziere die Gleichung mit durch:
Rest
11.1
Lagrange-Inversion
- Zu mit Umgebungen sei eine biholomorphe Funktion.
- Für die Koeffizienten der Umkehrfunktion
- gibt es die Formel .
Setzt man , so ist und und es ist ,
wobei wegen der Biholomorphie ist. Nun ist
und das ist , wenn eine einfach geschlossene Kurve um ist.
Substituiert man , so ist
.
Da aus der Biholomorphie folgt, berechnet man hier das Residuum an einer Polstelle -ter Ordnung.
Also ist .