| ↑ Formelsammlung Mathematik |
Darstellung
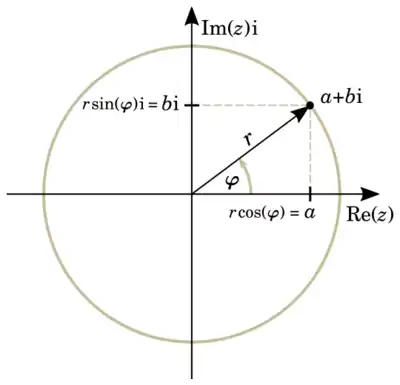
- Kartesische Form
- Polarform (trigonometrische Darstellung)
- Polarform (Exponentialdarstellung)
Elementare Operationen
| Name | Operation | Polarform | kartesische Form |
|---|---|---|---|
| Identität | |||
| Identität | |||
| Identität | |||
| Addition | |||
| Subtraktion | |||
| Multiplikation | |||
| Division | |||
| Kehrwert | |||
| Potenzierung | |||
| Konjugation | |||
| Realteil | |||
| Imaginärteil | |||
| Betrag | |||
| Argument |
Rechenweg zur Division:
Konjugation
Für alle gilt:
|
|
|
Für alle und gilt:
Argument
Für alle , und gilt:
Für alle gilt:
Potenzen
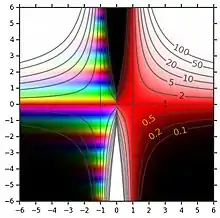
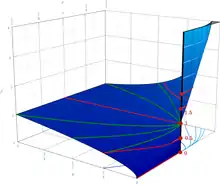
Definitionen:
Für alle gilt:
Für alle und gilt:
Für alle , und gilt:
Für alle , und gilt:
Wurzeln
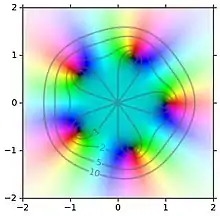
Sei . Für alle gilt:
Hauptwert:
Hauptwert, allgemein für :
Logarithmen
Definitionen:
Logarithmus als Urbild der Exponentialfunktion:
Für alle und gilt:
Für alle gilt:
Für alle gilt:
Für alle und gilt:
Aufgaben
Aufgabe 1
- Ist eine fest vorgegebene komplexe Zahl und ist eine komplexe Variable, so gilt für . (: Landau-Symbol)
Die Idee, in Betrag und Winkelanteil aufzuspalten (d. h. in Polarform zu bringen), führt zum Erfolg.
Sei und .
Es ist .
Somit gilt und daher
Nun ist aber beschränkt, weil , und positiv, weil .
Aufgabe 2
- Sind komplexe Zahlen mit positivem Realteil und ist irgendeine komplexe Zahl, so ist und .
besitzen Darstellungen mit .
Dann ist , und daher .
Aufgabe 3
- Ist eine komplexe Zahl, so ist .
Aufgabe 4
Aus
folgt .
Aufgabe 5
- , mit
Für jede von Null verschiedene komplexe Zahl gibt es stets zwei komplexe Zahlen die quadriert ergeben.
Mit soll der komplexe Hauptwert gemeint sein. Hier ist stets und im Fall ist .
Wenn sein soll, muss gelten und .
Daher ist
und ,
da im Fall sein muss. Und im Fall , somit , soll sein.
Die komplexen Zahlen werden in folgenden Büchern von Wikibooks behandelt:
- Imaginäre und komplexe Zahlen ist eine kompakte und abgeschlossene Darstellung des Themas durch Siegfried Petry in einem Band, die auf seiner Homepage weiter gepflegt wird.
- Komplexe Zahlen ist eine ausführlichere Darstellung mit einer stärkeren Gliederung und Ergänzungen.
Einzelne Kapitel anderer Bücher richten sich an bestimmte Zielgruppen: