Formelsammlung Mathematik: Finanzmathematik

↑ Formelsammlung Mathematik

Abkürzungen

Zinsfuß:

p

Zinssatz:

i={\frac {p}{100}}

Aufzinsungsfaktor:

r=1+i

Abzinsungsfaktor (Diskontierungsfaktor):

v={\frac {1}{r}}

Vorschüssiger Zins (Diskontrate):

d=1-v

Anfangskapital:

K_{0}

Endkapital (nach

n

Jahren):

K_{n}

Zinsrechnung

Zinseszins

Dekursive Zinsen:

K_{n}=K_{0}\cdot r^{n}

Antizipative Zinsen:

K_{0}=K_{n}\cdot v^{n}

Gemischte Verzinsung

Dekursive gemischte Verzinsung:

K_{n}=K_{0}\cdot r^{n}\cdot \left(1+{\frac {T}{360}}\cdot i\right)

Antizipative gemischte Verzinsung:

K_{0}=K_{n}\cdot v^{n}\cdot \left(1-{\frac {T}{360}}\cdot d\right)

Unterjährige Verzinsung

Effektiver Zinssatz:

i

Konformer Zinssatz:

i^{[m]}={\sqrt[{m}]{1+i}}-1\iff \left(1+i^{[m]}\right)^{m}=1+i

Proportionaler Zinssatz:

i^{\langle m\rangle }={\frac {i}{m}}\iff 1+m\cdot i^{\langle m\rangle }=1+i

Nomineller Zinssatz:

i^{(m)}=m\cdot i^{[m]}\iff \left(1+{\frac {i^{(m)}}{m}}\right)^{m}=1+i

Kontinuierlicher Zinssatz:

\varrho =\lim _{m\to \infty }i^{(m)}=i^{(\infty )}=\log(1+i)=\log(r)

Hierbei gelten folgende Ungleichungen:

i^{[m]}<i^{\langle m\rangle }\qquad \varrho <i^{(m)}<i\,

Annuität

Ein Kredit

K_{0}

wird über

n

Perioden hinweg mit dem Zinssatz

i

verzinst

und durch die Annuität

A

getilgt, so dass am Ende der Kassenbestand

K_{n}

ist.

Die Fälligkeit

F\in \{0,1\}

sei bei nachschüssiger Zahlweise

0

und bei verschüssiger Zahlweise

1

.

Aus der Rekursion

K_{m+1}=K_{m}\cdot r-A\cdot r^{F}

ergibt sich die Formel

K_{n}=K_{0}\cdot r^{n}-A\cdot {\frac {r^{n}-1}{i}}\cdot r^{F}

und damit

A={\frac {i}{r^{F}}}\cdot {\frac {K_{0}\cdot r^{n}-K_{n}}{r^{n}-1}}

.

In Excel gibt es die Funktion RMZ (Regelmäßige Zahlung)

{\text{RMZ(Zins;Zzr;Bw;Zw;F)}}={\frac {\text{Zins}}{(1+{\text{Zins}})^{\text{F}}}}\cdot {\frac {{\text{Bw}}\cdot (1+{\text{Zins}})^{\text{Zzr}}+{\text{Zw}}}{1-(1+{\text{Zins}})^{\text{Zzr}}}}

Rentenrechnung

E_{n}=R\cdot {\frac {r^{n}-1}{i}}

(Endwert bei nachschüssiger Rente)

E_{n}=R\cdot r\cdot {\frac {r^{n}-1}{i}}

(Endwert bei vorschüssiger Rente)

Intensität des Versicherungsschutzes

I={\frac {E}{S}}

, wobei

E

die Entschädigung für den Schaden

S

ist.

Abkürzungen

Anzahl der lebenden $x$ -Jährigen: $\ell _{x}$

Anzahl der im Alter $x$ Gestorbenen: $d_{x}=\ell _{x}-\ell _{x+1}$

Einjährige Überlebenswahrscheinlichkeit eines $x$ -Jährigen: $p_{x}={\frac {\ell _{x+1}}{\ell _{x}}}$

$n$ -jährige Überlebenswahrscheinlichkeit eines $x$ -Jährigen: ${}_{n}p_{x}=p_{x}\cdot p_{x+1}\dotsm p_{x+n-1}={\frac {\ell _{x+n}}{\ell _{x}}}$

Einjährige Sterbewahrscheinlichkeit eines $x$ -Jährigen: $q_{x}=1-p_{x}={\frac {d_{x}}{\ell _{x}}}$

$n$ -jährige Sterbewahrscheinlichkeit eines $x$ -Jährigen: ${}_{n}q_{x}=1-{}_{n}p_{x}$

Restlebenserwartung eines $x$ -Jährigen: $e_{x}={\frac {\ell _{x}+\ell _{x+1}+\dotsb +\ell _{\omega }}{\ell _{x}}}-{\frac {1}{2}}$

Stationaritätsbedingung

{}_{n+k}p_{x}={}_{k}p_{x}\cdot {}_{n}p_{x+k}

Beweis

${}_{n+k}p_{x}={\frac {\ell _{x+n+k}}{\ell _{x}}}={\frac {\ell _{x+k}}{\ell _{x}}}\cdot {\frac {\ell _{x+n+k}}{\ell _{x+k}}}={}_{k}p_{x}\cdot {}_{n}p_{x+k}$

Monatliche Sterblichkeit

q_{x}^{\text{mon}}>{\frac {q_{x}}{12}}

Beweis

$1-q_{x}=p_{x}=\left(p_{x}^{\text{mon}}\right)^{12}=\left(1-q_{x}^{\text{mon}}\right)^{12}>1-12q_{x}^{\text{mon}}$ (Bernoullische Ungleichung)

$\Rightarrow \,q_{x}<12q_{x}^{\text{mon}}\,\Rightarrow \,q_{x}^{\text{mon}}>{\frac {q_{x}}{12}}$

Kommutationswerte

Diskontierte Tote: $C_{x}=d_{x}\cdot v^{x+1}$	Diskontierte Lebende: $D_{x}=\ell _{x}\cdot v^{x}$
Aufsummierte diskontierte Tote: $M_{x}=C_{x}+C_{x+1}+\dotsb +C_{\omega }$	Aufsummierte diskontierte Lebende: $N_{x}=D_{x}+D_{x+1}+\dotsb +D_{\omega }$
Doppelt aufsummierte diskontierte Tote: $R_{x}=M_{x}+M_{x+1}+\dotsb +M_{\omega }$	Doppelt aufsummierte diskontierte Lebende: $S_{x}=N_{x}+N_{x+1}+\dotsb +N_{\omega }$

Barwerte

Reine Erlebensfallversicherung auf n Jahre für einen x-Jährigen

{}_{n}E_{x}={}_{n}p_{x}\cdot v^{n}={\frac {D_{x+n}}{D_{x}}}

Beweis

${}_{n}E_{x}={}_{n}p_{x}\cdot v^{n}={\frac {\ell _{x+n}}{\ell _{x}}}\cdot {\frac {v^{x+n}}{v^{x}}}={\frac {D_{x+n}}{D_{x}}}$

Vorschüssige n-jährige Zeitrente mit m Jahren Aufschubzeit

{}_{m|}{\ddot {a}}_{{\overline {n}}|}=\sum _{k=0}^{n-1}v^{m+k}={\frac {v^{m}-v^{m+n}}{d}}

Beweis

Geometrische Reihe

Nachschüssige n-jährige Zeitrente mit m Jahren Aufschubzeit

{}_{m|}a_{{\overline {n}}|}=\sum _{k=1}^{n}v^{m+k}={\frac {v^{m}-v^{m+n}}{i}}

Beweis

Geometrische Reihe

Vorschüssige n-jährige Rente für einen x-Jährigen mit m Jahren Aufschubzeit

{}_{m|}{\ddot {a}}_{x,{\overline {n}}|}=\sum _{k=0}^{n-1}{}_{m+k}p_{x}\cdot v^{m+k}={\frac {N_{x+m}-N_{x+m+n}}{D_{x}}}

Beweis

${}_{m|}{\ddot {a}}_{x,{\overline {n}}|}=\sum _{k=0}^{n-1}{}_{m+k}p_{x}\cdot v^{m+k}=\sum _{k=0}^{n-1}{\frac {\ell _{x+m+k}}{\ell _{x}}}\cdot {\frac {v^{x+m+k}}{v^{x}}}={\frac {1}{D_{x}}}\sum _{k=0}^{n-1}D_{x+m+k}={\frac {N_{x+m}-N_{x+m+n}}{D_{x}}}$

Nachschüssige n-jährige Rente für einen x-Jährigen mit m Jahren Aufschubzeit

{}_{m|}a_{x,{\overline {n}}|}=\sum _{k=1}^{n}{}_{m+k}p_{x}\cdot v^{m+k}={\frac {N_{x+m+1}-N_{x+m+n+1}}{D_{x}}}

Beweis

${}_{m|}a_{x,{\overline {n}}|}=\sum _{k=1}^{n}{}_{m+k}p_{x}\cdot v^{m+k}=\sum _{k=1}^{n}{\frac {\ell _{x+m+k}}{\ell _{x}}}\cdot {\frac {v^{x+m+k}}{v^{x}}}={\frac {1}{D_{x}}}\sum _{k=1}^{n}D_{x+m+k}={\frac {N_{x+m+1}-N_{x+m+n+1}}{D_{x}}}$

n-jährige Risikolebensversicherung für einen x-Jährigen mit m Jahren Aufschubzeit

Gemeint ist, dass in den ersten

m

Jahren kein Versicherungsschutz besteht,

und nicht, dass Hinterbliebene bei Eintritt des Versicherungsfalles m Jahre auf ihre Leistung warten müssen.

{}_{m|n}A_{x}=\sum _{k=0}^{n-1}{}_{m+k}p_{x}\cdot q_{x+m+k}\cdot v^{m+k+1}={\frac {M_{x+m}-M_{x+m+n}}{D_{x}}}

Beweis

${}_{m|n}A_{x}=\sum _{k=0}^{n-1}\!_{m+k}p_{x}\cdot q_{x+m+k}\cdot v^{m+k+1}=\sum _{k=0}^{n-1}{\frac {\ell _{x+m+k}}{\ell _{x}}}\cdot {\frac {d_{x+m+k}}{\ell _{x+m+k}}}\cdot v^{m+k+1}$

$=\sum _{k=0}^{n-1}{\frac {d_{x+m+k}}{\ell _{x}}}\cdot {\frac {v^{x+m+k+1}}{v^{x}}}={\frac {1}{D_{x}}}\cdot \sum _{k=0}^{n-1}C_{x+m+k}={\frac {M_{x+m}-M_{x+m+n}}{D_{x}}}$

n-jährige gemischte Versicherung für einen x-Jährigen

A_{x,{\overline {n}}|}={}_{|n}A_{x}+{}_{n}E_{x}={\frac {M_{x}-M_{x+n}}{D_{x}}}+{\frac {D_{x+n}}{D_{x}}}=1-(1-v)\cdot {\ddot {a}}_{x,{\overline {n}}|}

Beweis

In der Formel $A_{x,{\overline {n}}|}={}_{|n}A_{x}+{}_{n}E_{x}$ ersetze ${}_{|n}A_{x}$ durch $v\,{\ddot {a}}_{x,{\overline {n}}|}-a_{x,{\overline {n}}|}$ .

$A_{x,{\overline {n}}|}=v\,{\ddot {a}}_{x,{\overline {n}}|}-\left(a_{x,{\overline {n}}|}-{}_{n}E_{x}\right)$

Wegen $1+a_{x,{\overline {n}}|}={\ddot {a}}_{x,{\overline {n}}|}+{}_{n}E_{x}$ bzw. $a_{x,{\overline {n}}|}-{}_{n}E_{x}={\ddot {a}}_{x,{\overline {n}}|}-1$

ist nun $A_{x,{\overline {n}}|}=v\,{\ddot {a}}_{x,{\overline {n}}|}-\left({\ddot {a}}_{x,{\overline {n}}|}-1\right)=1-(1-v)\cdot {\ddot {a}}_{x,{\overline {n}}|}$ .

Linear steigende vorschüssige n-jährige Rente für einen x-Jährigen

(I{\ddot {a}})_{x,{\overline {n}}|}=\sum _{k=0}^{n-1}{}_{k}p_{x}\cdot (k+1)\cdot v^{k}={\frac {S_{x}-S_{x+n}-n\cdot N_{x+n}}{D_{x}}}

Beweis

$(I{\ddot {a}})_{x,{\overline {n}}|}=\sum _{k=0}^{n-1}{}_{k}p_{x}\cdot (k+1)\cdot v^{k}=\sum _{k=0}^{n-1}(k+1)\cdot {\frac {\ell _{x+k}}{\ell _{x}}}\cdot {\frac {v^{x+k}}{v^{x}}}={\frac {1}{D_{x}}}\sum _{k=0}^{n-1}(k+1)\,D_{x+k}$

$={\frac {1}{D_{x}}}\left(D_{x}+2D_{x+1}+\dotsb +n\,D_{x+n-1}\right)={\frac {1}{D_{x}}}\left[(D_{x}+\dotsb +D_{x+n-1})+(D_{x+1}+\dotsb +D_{x+n-1})+\dotsb +D_{x+n-1}\right]$

$={\frac {1}{D_{x}}}\left[(N_{x}-N_{x+n})+(N_{x+1}-N_{x+n})+\dotsb +(N_{x+n-1}-N_{x+n})\right]$

$={\frac {1}{D_{x}}}\left[N_{x}+N_{x+1}+\dotsb +N_{x+n-1}-n\,N_{x+n}\right]={\frac {S_{x}-S_{x+n}-n\cdot N_{x+n}}{D_{x}}}$

Linear steigende nachschüssige n-jährige Rente für einen x-Jährigen

(Ia)_{x,{\overline {n}}|}=\sum _{k=1}^{n}{}_{k}p_{x}\cdot k\cdot v^{k}={\frac {S_{x+1}-S_{x+n+1}-n\cdot N_{x+n+1}}{D_{x}}}

Beweis

$(Ia)_{x,{\overline {n}}|}=\sum _{k=1}^{n}{}_{k}p_{x}\cdot k\cdot v^{k}=\sum _{k=0}^{n}k\cdot {\frac {\ell _{x+k}}{\ell _{x}}}\cdot {\frac {v^{x+k}}{v^{x}}}={\frac {1}{D_{x}}}\sum _{k=1}^{n}k\cdot D_{x+k}$

$={\frac {1}{D_{x}}}\left(D_{x+1}+2D_{x+2}+\dotsb +n\,D_{x+n}\right)={\frac {1}{D_{x}}}\left[(D_{x+1}+\dotsb +D_{x+n})+(D_{x+2}+\dotsb +D_{x+n})+\dotsb +D_{x+n}\right]$

$={\frac {1}{D_{x}}}\left[(N_{x+1}-N_{x+n+1})+(N_{x+2}-N_{x+n+1})+\dotsb +(N_{x+n}-N_{x+n+1})\right]$

$={\frac {1}{D_{x}}}\left[N_{x+1}+N_{x+2}+\dotsb +N_{x+n}-n\,N_{x+n+1}\right]={\frac {S_{x+1}-S_{x+n+1}-n\cdot N_{x+n+1}}{D_{x}}}$

Linear steigende n-jährige Risikolebensversicherung für einen x-Jährigen

{}_{|n}(IA)_{x}=\sum _{k=0}^{n-1}{}_{k}p_{x}\cdot q_{x+k}\cdot (k+1)\cdot v^{k+1}={\frac {R_{x}-R_{x+n}-n\cdot M_{x+n}}{D_{x}}}

Beweis

${}_{|n}(IA)_{x}=\sum _{k=0}^{n-1}{}_{k}p_{x}\cdot q_{x+k}\cdot (k+1)\cdot v^{k+1}=\sum _{k=0}^{n-1}(k+1)\cdot {\frac {\ell _{x+k}}{\ell _{x}}}\cdot {\frac {d_{x+k}}{\ell _{x+k}}}\cdot {\frac {v^{x+k+1}}{v^{x}}}={\frac {1}{D_{x}}}\sum _{k=0}^{n-1}(k+1)\cdot C_{x+k}$

$={\frac {1}{D_{x}}}\left(C_{x}+2C_{x+1}+\dotsb +n\,C_{x+n-1}\right)={\frac {1}{D_{x}}}\left[(C_{x}+\dotsb +C_{x+n-1})+(C_{x+1}+\dotsb +C_{x+n-1})+\dotsb +C_{x+n-1}\right]$

$={\frac {1}{D_{x}}}\left[(M_{x}-M_{x+n})+(M_{x+1}-M_{x+n})+\dotsb +(M_{x+n-1}-M_{x+n})\right]$

$={\frac {1}{D_{x}}}\left[M_{x}+M_{x+1}+\dotsb +M_{x+n-1}-n\,M_{x+n}\right]={\frac {R_{x}-R_{x+n}-n\cdot M_{x+n}}{D_{x}}}$

Deckungskapital

{}_{m}V_{x}^{({\text{re}})}={}_{m}V_{x}^{({\text{pro}})}

Beweis

Bei einem $n$ -jährigen Lebensversicherungsvertrag zahlt der Versicherte im $k$ -ten Versicherungsjahr vorschüssig (zu Beginn des $k$ -ten Jahres) den Beitrag $B_{k}$ .
Stirbt der Versicherte im $k$ -ten Versicherungsjahr (d.h. er stirbt im Alter $x+k-1$ ), zahlt die Versicherung nachschüssig (also am Ende des $k$ -ten Jahres) die Todesfallleistung $T_{k}$ .
Überlebt der Versicherte das $k$ -te Versicherungsjahr (d.h. er erlebt das $(k+1)$ -te Jahr), zahlt die Versicherung nachschüssig die Erlebensfallleistung $E_{k}$ .

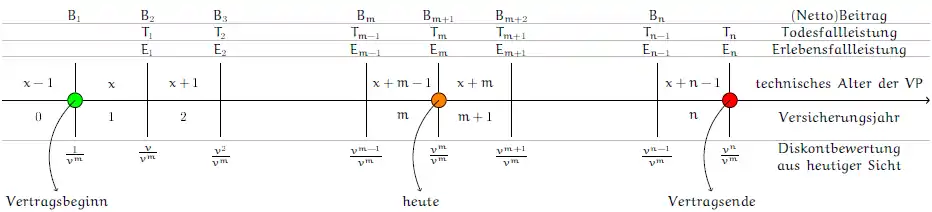
Zu Vertragsbeginn $(m=0)$ sieht man den Kapitalwert der zukünftigen Beiträge und Leistungen wie folgt:

${}_{0}B_{x}^{({\text{pro}})}=\sum _{k=0}^{n-1}\,_{k}p_{x}\cdot B_{k+1}\cdot v^{k}$

${}_{0}T_{x}^{({\text{pro}})}=\sum _{k=0}^{n-1}\,_{k}p_{x}\cdot q_{x+k}\cdot T_{k+1}\cdot v^{k+1}$

${}_{0}E_{x}^{({\text{pro}})}=\sum _{k=0}^{n-1}{}_{k+1}p_{x}\cdot E_{k+1}\cdot v^{k+1}$

Die vereinbarten Beiträge und Leistungen $B_{k},T_{k},E_{k}$ müssen dabei so gewählt sein, dass das Äquivalenzprinzip erfüllt ist:

${}_{0}B_{x}^{({\text{pro}})}={}_{0}T_{x}^{({\text{pro}})}+{}_{0}E_{x}^{({\text{pro}})}$

Am Ende des $m$ -ten Versicherungsjahres sieht man den zukünftigen Beitrags- und Leistungskapitalwert wie folgt:

${}_{m}B_{x}^{({\text{pro}})}=r^{m}\sum _{k=m}^{n-1}\;_{k}p_{x}\cdot B_{k+1}\cdot v^{k}=r^{m}\sum _{k=0}^{n-m-1}{}_{m+k}p_{x}\cdot B_{m+k+1}\cdot v^{m+k}=\;_{m}p_{x}\sum _{k=0}^{n-m-1}{}_{k}p_{x+m}\cdot B_{m+k+1}\cdot v^{k}$

${}_{m}T_{x}^{({\text{pro}})}=r^{m}\sum _{k=m}^{n-1}\;_{k}p_{x}\cdot q_{x+k}\cdot T_{k+1}\cdot v^{k+1}=r^{m}\sum _{k=0}^{n-m-1}{}_{m+k}p_{x}\cdot q_{m+k}\cdot T_{m+k+1}\cdot v^{m+k+1}={}_{m}p_{x}\sum _{k=0}^{n-m-1}{}_{k}p_{x+m}\cdot q_{x+m+k}\cdot T_{m+k+1}\cdot v^{k+1}$

${}_{m}E_{x}^{({\text{pro}})}=r^{m}\sum _{k=m}^{n-1}{}_{k+1}p_{x}\cdot E_{k+1}\cdot v^{k+1}=r^{m}\sum _{k=0}^{n-m-1}{}_{m+k+1}p_{x}\cdot E_{m+k+1}\cdot v^{m+k+1}={}_{m}p_{x}\sum _{k=0}^{n-m-1}{}_{k+1}p_{x+m}\cdot E_{m+k+1}\cdot v^{k+1}$

Am Ende des $m$ -ten Versicherungsjahres sieht man den vergangenen Beitrags- und Leistungskapitalwert wie folgt:

${}_{m}B_{x}^{({\text{re}})}=r^{m}\sum _{k=0}^{m-1}{}_{k}p_{x}\cdot B_{k+1}\cdot v^{k}$

${}_{m}T_{x}^{({\text{re}})}=r^{m}\sum _{k=0}^{m-1}{}_{k}p_{x}\cdot q_{x+k}\cdot T_{k+1}\cdot v^{k+1}$

${}_{m}E_{x}^{({\text{re}})}=r^{m}\sum _{k=0}^{m-1}{}_{k+1}p_{x}\cdot E_{k+1}\cdot v^{k+1}$

Das prospektive Deckungskapital ist die Differenz zwischen ausstehendem Leistungskapitalwert und ausstehendem Beitragskapitalwert.

${}_{m}V_{x}^{({\text{pro}})}={}_{m}T_{x}^{({\text{pro}})}+{}_{m}E_{x}^{({\text{pro}})}-{}_{m}B_{x}^{({\text{pro}})}$

Das retrospektive Deckungskapital ist die Differenz zwischen erbrachtem Beitragskapitalwert und angefallenem Leistungskapitalwert.

${}_{m}V_{x}^{({\text{re}})}={}_{m}B_{x}^{({\text{re}})}-{}_{m}T_{x}^{({\text{re}})}-{}_{m}E_{x}^{({\text{re}})}$

Nach dem Äquivalenzprinzip ist der Kapitalwert aller vergangenen und zukünftigen Beiträge gleich dem Kapitalwert aller vergangenen und zukünftigen Leistungen.

${}_{m}B_{x}^{({\text{re}})}+{}_{m}B_{x}^{({\text{pro}})}={}_{m}T_{x}^{({\text{re}})}+{}_{m}T_{x}^{({\text{pro}})}+{}_{m}E_{x}^{({\text{re}})}+{}_{m}E_{x}^{({\text{pro}})}$

Daraus folgt

${}_{m}B_{x}^{({\text{re}})}-{}_{m}T_{x}^{({\text{re}})}-{}_{m}E_{x}^{({\text{re}})}={}_{m}T_{x}^{({\text{pro}})}+{}_{m}E_{x}^{({\text{pro}})}-{}_{m}B_{x}^{({\text{pro}})}$ ,

also gerade

${}_{m}V_{x}^{({\text{re}})}={}_{m}V_{x}^{({\text{pro}})}$ .

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.