| ↑ Formelsammlung Mathematik |
Summe ersten natürlichen Zahlen (Gaußsche Summenformel)
Beweismethode: Vollständige Induktion; der ausführliche Beweis ist unter der Gaußschen Summenformel dargestellt.
Summe ersten ungeraden Zahlen
Summe der ersten Quadratzahlen
Beweismethode: Induktionsbeweis
Oder direkt wie folgt:
Mit gilt:
Es existieren Teilsummen, die bei jedem Schritt jeweils um eine zusätzliche Zahl ergänzt werden. Damit kann die Anzahl der einzelnen Zahlen gezählt werden. Es ergibt sich, dass -mal die Zahl auftritt, dann die Zahl usw. und schließlich einmal die Zahl , d.h.
Damit ergibt sich:
Daraus folgt:
Womit schließlich folgt:
Euler-Maclaurinsche Summenformel
- Sind ganze Zahlen, so dass ist, und ist eine -mal stetig differenzierbare Funktion, so gilt
- .
- Hierbei steht für das -te periodische Bernoulli-Polynom und für die -te Bernoulli-Zahl.
Damit ist der Induktionsanfang für gemacht.
Wegen ist
.
Dies ist der Induktionsschluß.
[Umformung der Potenzsumme]
Faulhabersche Formel
Einerseits ist
.
Andererseits ist
.
Durch Koeffizientenvergleich ergibt sich
.
Das Einschieben des Vorzeichenoperators ändert nur den Summanden zum Laufindex k=1.
Aus wird .
Also ist .
In der Euler-Maclaurinschen Summenformel
setze und .
Wegen verschwindet der letzte Term und es gilt
.
Der letzte Summand der Reihe (Laufindex ) verschwindet, da und jeweils gleich sind.
Also ist
.
Verallgemeinerte faulhabersche Formel
[Harmonische Zahlen]
Nach der verallgemeinerten Faulhaberschen Formel ist
.
Führt man den Grenzprozess durch, so ist ,
und .
[Bernoulli-Zahlen]
Partialsummen der geometrischen Reihe
- für , sonst divergent
ergibt die Teleskopsumme , und das ist .
Korollar zu den Partialsummen der geometrischen Reihe
Man verwendet die Formel und wendet auf beiden Seiten an. Das wird so oft wiederholt, bis der Koeffizient in der Summe ist.
Binomischer Lehrsatz
Der Induktionsanfang ist klar.
Induktionsschritt:
lässt sich durch Ausmultiplizieren wie folgt als Summe von zwei Reihen schreiben:
Wegen für ändert sich am Wert der ersten Reihe nichts, wenn bis läuft.
Die zweite Reihe lässt sich nach Indexverschiebung schreiben als .
Wegen für ändert sich am Wert der zweiten Reihe nichts, wenn man mit zu summieren beginnt.
Es ist also .
Und wegen ist dies gleich .
1. Korollar zum Binomischem Lehrsatz
Das Ergebnis ergibt sich sofort aus dem Binomischen Lehrsatz für .
2. Korollar zum Binomischem Lehrsatz
Das Ergebnis ergibt sich sofort aus dem Binomischen Lehrsatz für und .
3. Korollar zum Binomischem Lehrsatz
Es gilt:
Daraus folgt:
Leibniz-Regel
Der Induktionsbeweis ist analog zum Induktionsbeweis des Binomisches Lehrsatzes.
[Wert der Beta-Funktion]
Iterierter Differenzenoperator
- Steht für den Differenzenoperator, definiert durch ,
- so gilt .
Der Induktionsbeweis hierzu ist analog zum Beweis des Binomischen Lehrsatzes.
Eulersche Identität
Ist der Differenzenoperator, definiert durch ,
so ist .
Wiederholtes Anwenden des Differenzenoperators liefert .
Für gilt insbesondere .
Setzt man in der Formel
, so erhält man die eulersche Identität.
[Summe der cos(kx)]
Aus dem Vergleich der Realteile ergibt sich die Behauptung.
Aus der 2. prosthaphäretischen Formel nach Werner folgt
.
Daraus ergibt sich die Teleskopsumme
Und das ist nach der 1. prosthaphäretischen Formel nach Simpson gleich
.
[Summe der sin(kx)]
Aus dem Vergleich der Imaginärteile ergibt sich die Behauptung.
Aus der 4. prosthaphäretischen Formel nach Werner folgt
.
Daraus ergibt sich die Teleskopsumme
Und das ist nach der 4. prosthaphäretischen Formel nach Simpson gleich
.
[Iterierter Operator (x d/dx) auf binomischen Lehrsatz]
Wende die Formel auf die Funktion an.
[Korollar zur letzten Formel]
Benutze die Formel .
Teile beide Seiten durch und führe den Grenzübergang durch.
[Geometrische Reihe mit Stirling-Zahlen, iterierter Operator (x d/dx)]
Rekursionsformel für die geraden Werte der Zeta-Funktion
- für
Ist , so gilt:
(Cauchy-Produkt)
Da ist, gilt
.
Durch Koeffizientenvergleich ergibt sich für .
Wegen sind der erste und letzte Summand jeweils .
Also ist .
[Potenzen von Kotangens, Summe über spezielle Stellen]
Verallgemeinerte Gauß-Summe
- gerade
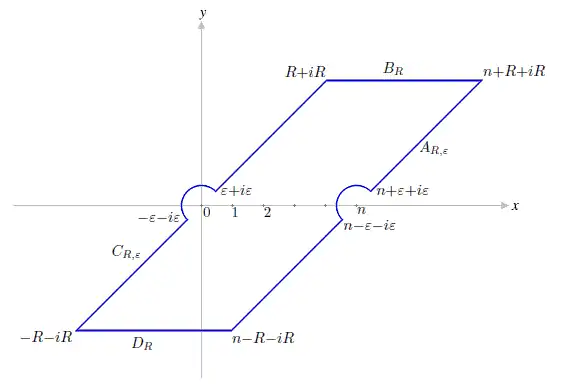
Für und mit geradem sei .
Für alle und gilt .
Es ist .
Die Integrale und verschwinden also für .
Wegen
ist
eine auf holomorphe Funktion mit hebbaren Singularitäten in .
.
Da letzter Integrand nur hebbare Singularitäten besitzt, stimmt das Integral für überein mit
.
Landsberg-Schaar Relation
- oder gerade
- und ungerade
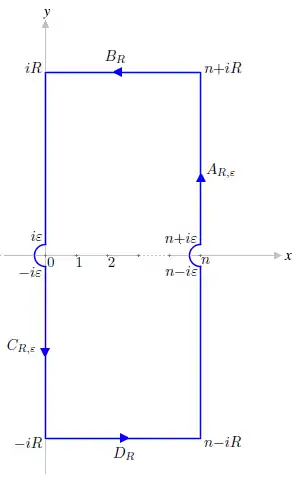
Für mit gerade sei .
Für alle und gilt .
Ist , so gilt für .
Die Integrale und verschwinden also für .
Wegen
ist
eine auf holomorphe Funktion mit hebbaren Singularitäten in .
.
Da letzter Integrand nur hebbare Singularitäten besitzt, stimmt das Integral für überein mit
.
Gauß-Summe
In der Landsberg-Schaar Relation setze .
[Kosekansquadrate, Summe über spezielle Stellen]
Verwende die Formel .
Wende auf beiden Seiten den Logarithmus an:
Differenziere nach :
Differenziere nochmal nach :
[Tangensquadrate, Summe über spezielle Stellen]
Vergleiche die Realteile auf beiden Seiten:
Daraus folgt unmittelbar .
Der Ausdruck auf der linken Seite verschwindet für .
Also hat das Polynom die Nullstellen .
Nach dem Satz von Vieta ist die negative Summe aller Nullstellen gleich dem Koeffizient vor dem ,
nämlich .
[Kosekans, alternierende Summe über spezielle Stellen]
,
wobei die Tschebyscheff Polynome zweiter Art sind.
Wegen
ist .
Nach dem Satz von Vieta ist .
Und das ist
.
Partielle Summation
Daraus ergibt sich die Teleskopsumme
.
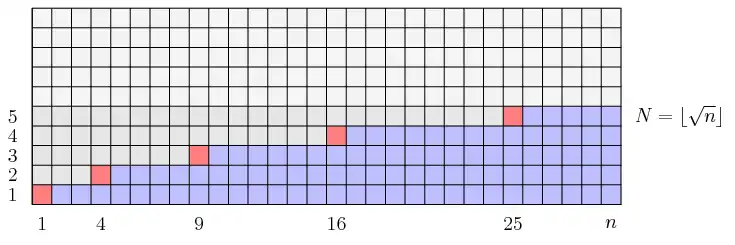
[Summe von abgerundeten Quadratwurzeln]
[Sinus, Summe über spezielle Stellen]
Setzt man , so ist .
Also ist .
Nach partieller Summation ist
.
Dabei ist .
,
wobei ist. Somit ist .
Also ist .