| ↑ Formelsammlung Mathematik |
| → Vektorrechnung |
Geraden
Parameterdarstellung
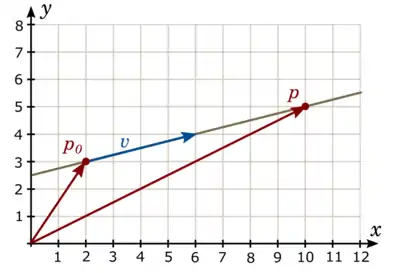
mit , und .
In einem verschobenen Koordinatensystem bekommen die Ortsvektoren und (rot) andere Koordinaten. Die Koordinaten des Richtungsvektors (blau) bleiben jedoch erhalten, sofern das Koordinatensystem nicht gedreht wird.
Punktrichtungsform:
| der Parameter | |
| der Stützpunkt | |
| für jedes ein Punkt auf der Gerade | |
| der Richtungsvektor | |
| Verschiebungsvektoren | |
| die Gerade |
Punktrichtungsform für die Ebene:
Punktrichtungsform für den Raum:
Gerade durch zwei Punkte: Sind zwei Punkte mit , so ist durch diese Punkte eine Gerade gegeben. Man setzt und . Nach Umformung ergibt sich die Zweipunkteform.
Zweipunkteform:
Zweipunkteform für die Ebene:
Hierbei handelt es sich um eine Affinkombination.
Für ist es eine Konvexkombination: eine Parameterdarstellung für die Strecke von nach .
Parameterfreie Darstellung
Hesse-Form:
: Stützpunkt, : Normalenvektor.
Die Hesse-Form ist nur in der Ebene möglich. In Koordinaten ergibt sich
Hesse-Normalform: Hesse-Form mit .
Sei das äußere Produkt.
Plückerform:
Die Größe heißt Moment. Beim Tupel handelt es sich um Plückerkoordinaten für die Gerade.
In der Ebene gilt speziell:
mit .
Sei und sowie . Aus der letzten Gleichung ergibt sich:
Im Raum ergibt sich ein Gleichungssystem:
mit .
Abstand Punkt zu Gerade
Sei die Punktrichtungsform einer Geraden und sei ein weiterer Punkt. Bei handelt es sich um den Abstandsvektor in Abhängigkeit von .
Ansatz: Es gibt genau ein , so dass gilt:
Lösung:
Ebenen
Parameterdarstellung
Seien zwei nicht kollineare Vektoren.
Punktrichtungsform:
Parameterfreie Darstellung
Seien zwei nicht kollineare Vektoren. Durch
wird eine Ebene beschrieben. Hiermit kann auch eine Ebene im höherdimensionalen Raum beschrieben werden, es ergibt sich dann aber ein lineares Gleichungssystem.
Hesse-Form:
: Stützpunkt, : Normalenvektor. Die Hesse-Form einer Ebene ist nur im dreidimensionalen Raum möglich.
Den Normalenvektor bekommt man aus der Punktrichtungsform der Ebene mit
- .
Es gilt
Über den Zusammenhang , und ergibt sich die
Koordinatenform:
Abstand Punkt zu Ebene
Sei die Punktrichtungsform einer Ebene und sei ein weiterer Punkt. Bei handelt es sich um den Abstandsvektor in Abhängigkeit von .
Ansatz: Es gibt genau ein Tupel , so dass gilt:
Lösung: Es ergibt sich ein LGS:
mit
Die Lösung des LGS ist: