| ↑ Formelsammlung Mathematik |
Rechenregeln
Binomische Formeln
Sei ein Ring, z. B. oder . Sei und . Dann gilt:
| (erste binomische Formel) | |
|---|---|
| (zweite binomische Formel) | |
| (dritte binomische Formel) |
und:
Binomischer Lehrsatz
Sei ein unitärer Ring, z. B. oder . Sei und . Dann gilt:
| usw. | usw. |
Pascalsches Dreieck
Das pascalsche Dreieck ist eine Wertetabelle für die Binomialkoeffizienten
| k=0 | k=1 | k=2 | k=3 | k=4 | k=5 | k=6 | k=7 | k=8 | |
|---|---|---|---|---|---|---|---|---|---|
| n=0 | 1 | ||||||||
| n=1 | 1 | 1 | |||||||
| n=2 | 1 | 2 | 1 | ||||||
| n=3 | 1 | 3 | 3 | 1 | |||||
| n=4 | 1 | 4 | 6 | 4 | 1 | ||||
| n=5 | 1 | 5 | 10 | 10 | 5 | 1 | |||
| n=6 | 1 | 6 | 15 | 20 | 15 | 6 | 1 | ||
| n=7 | 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 | |
| n=8 | 1 | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 |
Das Dreieck lässt sich rekursiv durch die Vorschrift
erzeugen.
Multinomialtheorem
Sei ein unitärer Ring. Sei , wobei die paarweise kommutieren. Es gilt
In Multiindex-Notation:
mit
Die ersten Formeln sind:
| n=2 | (a+b)2 | = a2 + b2 + 2ab |
|---|---|---|
| (a+b+c)2 | = a2 + b2 + c2 + 2ab + 2ac + 2bc | |
| (a+b+c+d)2 | = a2 + b2 + c2 + d2 + 2ab + 2ac + 2ad + 2bc + 2bd + 2cd | |
| n=3 | (a+b)3 | = a3 + b3 + 3a2b + 3b2a |
| (a+b+c)3 | = a3 + b3 + c3 + 3a2b + 3a2c + 3b2a + 3b2c + 3c2a + 3c2b + 6abc |
Potenzen
| usw. |
Definition für und :
Für :
Definition für und :
Für :
Potenzgesetze
Für und gilt:
Ist zusätzlich , so gilt:
Für und gilt:
| → Potenzgesetze für komplexen Zahlen |
Logarithmen
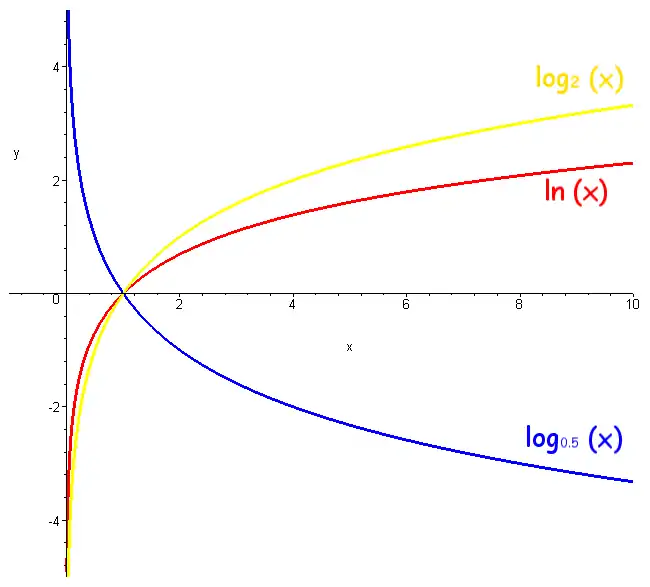
Für mit und gilt:
Logarithmengesetze
Für mit und gilt:
Welcher Logarithmus verwendet wird, ist unerheblich. D. h. man setzt für ein festes mit und . Meistens ist oder .
Spezielle Logarithmen
| Bezeichnung | Definierende Eigenschaft |
Basis | |
|---|---|---|---|
| Natürliche Logarithmen | ln | e=2,718 281 828 459 045... (eulersche Zahl) | |
| Dekadische Logarithmen | lg | 10 | |
| Binäre Logarithmen | lb, ld | 2 |
| → Logarithmengesetze für komplexe Zahlen |
Gleichungen
Definition
Sind zwei auf der Grundmenge definierte Funktionen, so nennt man
eine Bestimmungsgleichung, wenn die Lösungsmenge
gesucht ist.
Bei kann es sich auch um eine Menge von Tupeln handeln:
- usw.
Man schreibt auch oder usw.
Äquivalenzumformungen
Äquivalenzumformungen lassen die Lösungsmenge einer Gleichung unverändert.
Seien zwei Aussageformen.
| Äquivalenz | Implikation |
|---|---|
|
Gilt für alle : so gilt: |
Gilt für alle : so gilt: |
Seien Funktionen mit Definitionsbereich und Zielmenge oder .
Für alle x gilt:
Besitzt keine Nullstellen, so gilt für alle x:
Besitzt Nullstellen, so gilt immerhin noch für alle x:
Ist eine auf dem Definitionsbereich injektive Funktion, dann gilt für alle x:
Jede streng monotone Funktion ist injektiv.
Arten von Gleichungen
Polynomgleichungen