Das Frenetsche Dreibein

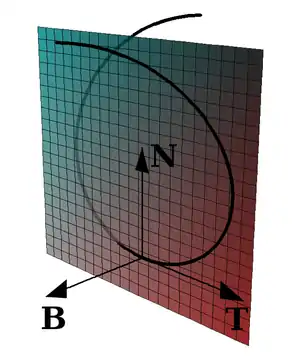
Kurve mit den drei Vektoren des Frenetschen Dreibeins

Berechnung

Definition des Frenetschen Dreibeins
${\displaystyle {\vec {v}}_{1}={\frac {\mathrm {d} {\vec {x}}}{\mathrm {d} s}}={\vec {x}}'(s)}$ Tangentenvektor ${\displaystyle {\vec {v}}_{2}={\frac {{\vec {x}}''(s)}{\|{\vec {x}}''(s)\|}}}$ Hauptnormalenvektor ${\displaystyle {\vec {v}}_{3}={\vec {v}}_{1}\times {\vec {v}}_{2}}$ Binormalenvektor

Des Weiteren wird durch ${\displaystyle {\vec {v}}_{1}}$ und ${\displaystyle {\vec {v}}_{2}}$ die Schmiegebene und durch ${\displaystyle {\vec {v}}_{2}}$ und ${\displaystyle {\vec {v}}_{3}}$ die Normalebene in jedem Kurvenpunkt, der die Voraussetzung erfüllt, aufgespannt. Sie steht senkrecht zur Kurvenbahn. Die Vektorkombination aus ${\displaystyle {\vec {v}}_{1}}$ und ${\displaystyle {\vec {v}}_{3}}$ spannt die Streckebene oder rektifizierende Ebene auf.

Zurück zu Torsion | Hoch zu Inhaltsverzeichnis | Vor zu Parametrisierung der Flächen