Parametrisierung einer Flächenkurve nach der Bogenlänge / erste Fundamentalform

Herleitung der klassischen Darstellung

Für die Parametrisierung einer Flächenkurve nach der Bogenlänge wird derselbe Ansatz gewählt wie im Kapitel Kurventheorie.

s=\int _{t_{0}}^{t}\left\|{\dot {\vec {x}}}\right\|\,\mathrm {d} t

${\dot {\vec {x}}}={\frac {d{\vec {x}}}{dt}}$ unterscheidet sich allerdings, da ${\vec {x}}$ in Abhängigkeit von u und v gegeben ist und deswegen auch nach u und v abgeleitet wird.

{\frac {d{\vec {x}}}{dt}}={\frac {\partial {\vec {x}}}{\partial u}}{\frac {du(t)}{dt}}+{\frac {\partial {\vec {x}}}{\partial v}}{\frac {dv(t)}{dt}}

u(t) und v(t) sind die Funktionen (keine Vektoren!) mit denen die Flächenkurve auf der Fläche festgelegt wurde.

Das vollständige Differential in vereinfachter Schreibweise:

{\dot {\vec {x}}}={\vec {x}}_{u}\cdot {\dot {u}}+{\vec {x}}_{v}\cdot {\dot {v}}

Im Integral steht der Betrag des Vektors. Das bedeutet, daß das vollständige Differential im ersten Schritt quadriert werden muß. Dadurch entsteht ein langer Ausdruck:

({\dot {\vec {x}}})^{2}=({\vec {x}}_{u}\cdot {\dot {u}}+{\vec {x}}_{v}\cdot {\dot {v}})^{2}={\vec {x}}_{u}\cdot {\vec {x}}_{u}\cdot {\dot {u}}^{2}+2\cdot {\vec {x}}_{u}\cdot {\vec {x}}_{v}\cdot {\dot {u}}\cdot {\dot {v}}+{\vec {x}}_{v}\cdot {\vec {x}}_{v}\cdot {\dot {v}}^{2}

Üblicherweise werden Abkürzungen eingeführt, die Gaußsche Fundamentalgrößen genannt werden:

E={\vec {x}}_{u}\cdot {\vec {x}}_{u}

F={\vec {x}}_{u}\cdot {\vec {x}}_{v}

G={\vec {x}}_{v}\cdot {\vec {x}}_{v}

Das Integral sieht jetzt so aus:

s=\int _{t_{0}}^{t}{\sqrt {E{\dot {u}}^{2}+2F{\dot {u}}{\dot {v}}+G{\dot {v}}^{2}}}\,\mathrm {d} t

Durch Ableiten und anschließendes Quadrieren ergibt sich

\left({\frac {ds}{\mathrm {d} t}}\right)^{2}=E{\dot {u}}^{2}+2F{\dot {u}}{\dot {v}}+G{\dot {v}}^{2}

Multiplizieren mit $dt^{2}$ (steckt in ${\dot {u}}$ und ${\dot {v}}$ drin!) ergibt die metrische oder erste Fundamentalform:

Definition der ersten Fundamentalform
$ds^{2}=Edu^{2}+2Fdudv+Gdv^{2}$ $E={\vec {x}}_{u}\cdot {\vec {x}}_{u}$ $F={\vec {x}}_{u}\cdot {\vec {x}}_{v}$ $G={\vec {x}}_{v}\cdot {\vec {x}}_{v}$

Neue Darstellung

Definition der ersten Fundamentalform in neuer Schreibweise

$I=\mathrm {d} s^{2}=g_{\alpha \beta }\mathrm {d} (u^{\alpha })\mathrm {d} (u^{\beta })$

$\alpha =1,2$

$\beta =1,2$

Beim Einsetzen der Indizes werden alle möglichen Kombinationen aufaddiert. Dadurch entsteht die klassische Form.

Die römische I steht für die 'erste' Fundamentalform
Die indizierten gs werden als Gaußsche Fundamentalgrößen bezeichnet.
Die Gaußschen Flächenparameter u und v werden durch $(u^{\alpha })$ und $(u^{\beta })$ ersetzt.

(D.h. für $\alpha =2$ oder $\beta =2$ : $u^{\alpha }=u^{\beta }=(u^{2})$ bedeutet u mit Index 2 und nicht $u\cdot u$ )

erster Fundamentaltensor

Die neue Darstellung mit den Indizes kommt vom ersten Fundamentaltensor. Der Tensor ist eine Metrik.

\mathbf {G} ={\begin{pmatrix}g_{11}&g_{12}\\g_{21}&g_{22}\end{pmatrix}}

Bogenlängen der Parameterlinien

Die Bogenlängen der Parameterlinien (u=const bzw. v=const) lassen sich einfach mit Hilfe der Fundamentalformen berechnen:

für v=const:

s=\int {\sqrt {E}}\,\mathrm {d} u

für u=const:

s=\int {\sqrt {G}}\,\mathrm {d} v

Beispiel für Kugel

Für die zu Beginn des Kapitels Flächentheorie gegebene Parametrisierung der Kugel wird die erste Fundamentalform berechnet:

{\vec {x}}_{u}=-R\cdot \sin {u}\cdot \cos {v}\cdot {\vec {e_{x}}}+R\cdot \cos {u}\cdot \cos {v}\cdot {\vec {e_{y}}}

{\vec {x}}_{v}=-R\cdot \cos {u}\cdot \sin {v}\cdot {\vec {e_{x}}}-R\cdot \sin {u}\cdot \sin {v}\cdot {\vec {e_{y}}}+R\cdot \cos {v}\cdot {\vec {e_{z}}}

Fundamentalgrößen

E=R^{2}\cos ^{2}{v}

F=0

G=R^{2}

erste Fundamentalform

ds^{2}=R^{2}(\cos {v}^{2}du^{2}+dv^{2})

Erkenntnisse

Radius der Parameterlinien

Parameterlinien senkrecht

Aus der ersten Fundamentalform lässt sich für die Parameterlinien eine Erkenntnis ableiten. Da F, das aus einem Skalarprodukt entsteht, Null ist, stehen alle u-Parameterlinien senkrecht zu den v-Parameterlinien.

Radius der Parameterlinien

Aus den Wurzeln von E und G lassen sich, da F Null ist, weitere Erkenntnisse ableiten.

u-Parameterlinien

Alle u-Parameterlinien sind Kreise mit dem Radius ${\sqrt {G}}=R$ . Sie entsprechen den Meridianen mit fester Länge (u-Parameter) und variabler Breite (v-Parameter).

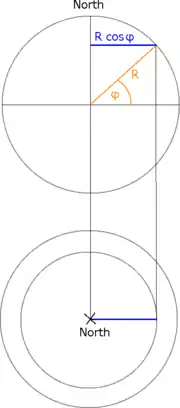
v-Parameterlinien

Die v-Parameterlinien haben feste Breite v bzw. $\phi$ . Die Länge u ist variabel. Jede Parameterlinie hat ihren eigenen Radius ${\sqrt {E}}=R\cos v$ .

Zurück zu Gaußsches Dreibein |

Hoch zu Inhaltsverzeichnis |

Vor zu Winkel zwischen Flächenkurven

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.