Algorithmensammlung: Zahlentheorie

• Euklidischer Algorithmus
• Sieb des Eratosthenes
• Primfaktorisierung
• Fibonacci-Folge
• Goldener Schnitt
• Signum

Definition des Goldenen Schnittes

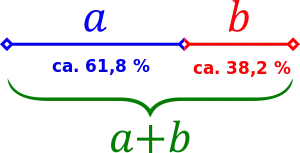
Gesucht werden zwei Zahlen für die folgende Gleichung gilt:

${\displaystyle {\frac {a}{b}}={\frac {(a+b)}{a}}}$

Das Verhältnis der beiden Zahlen ist der Goldene Schnitt. Das Verhältnis beider Zahlen ist ein konstanter Wert, der ungefähr 1,6 beträgt. Die größere Zahl ist etwa 1,6 mal größer als die kleinere Zahl. Aus einigen mathematischen Umformungen ergibt sich für den Goldenen Schnitt ein Wert von ${\displaystyle {\frac {1+{\sqrt {5}}}{2}}}$.

${\displaystyle {\begin{aligned}GS&={\frac {a}{b}}\\GS&={\frac {1+{\text{SQR(5)}}}{2}}\end{aligned}}}$

SQR ist die Abkürzung in Basic für Wurzel aus oder Squareroot. Der Zahlenwert, der das Verhältnis angibt, mit dem die Zahlen den Goldenen Schnitt erfüllen, heißt Goldene Zahl.

${\displaystyle GS=1,61803399\ldots }$

Andere Darstellung:

${\displaystyle {\frac {M}{m}}={\frac {M+m}{M}}}$

Der Goldene Schnitt hat einige besondere Eigenschaften und findet sich beispielsweise im gleichseitigen Fünfeck.

Konstruktion des Fünfecks mit dem Goldenen Schnitt

Basic C64

Das Programm berechnet erst den Wert der Goldenen Zahl (einer Konstanten). Gibt man dann einen beliebigen größeren Wert a ein, wird der dazu im Goldenen Schnitt stehende kleinere Wert b berechnet.

 10 REM GOLDENER SCHNITT
 20 GS = (1+SQR(5)) / 2
 30 PRINT GS
 40 INPUT A
 50 B = A / (1+SQR(5)) * 2
 60 PRINT B

Basic X11 Android

REM GOLDENER SCHNITT 
cls
GS = ( 1 + SQR(5)) /2 
PRINT GS 
INPUT A 
B = A/(1+SQR(5))*2 
PRINT "A = ";A,"B = ";B
print "A + B = ";a + b

Python

# Getestet unter Python 3.4, sollte aber unter allen 3.x-Versionen laufen

import math


gs = (1+math.sqrt(5)) / 2
print(gs)
a = float(input("Bitte A eingeben: "))  # Eingabe mit Punkt statt Komma!
b = a / (1+math.sqrt(5)) * 2
print("A = ", a, "B = ", b)
print("A + B = ", a+b)  # möglicherweise treten Rundungsfehler zutage