Schach/Springer/Äquivalenzklassen/Aufgabe/Lösung

Jeder Pferdsprung würde das ${}2\times 2$ -Brett verlassen, daher sind die vier einzelnen Felder die Äquivalenzklassen.
Vom zentralen Feld aus würde jeder Pferdsprung das ${}3\times 3$ -Brett verlassen, dieses bildet somit für sich eine Äquivalenzklasse. Die acht übrigen Felder sind mittels Pferdsprüngen untereinander verbindbar, wie die Skizze zeigt.
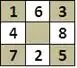
Die in der folgenden Matrix angegebene Zugreihenfolge
${\begin{pmatrix}1&6&15&10\\12&9&2&5\\7&4&11&14\\&13&8&3\end{pmatrix}}$

zeigt, dass alle Felder bis auf das links unten miteinander durch Pferdsprünge verbunden sind. Letzteres ist mit dem mit ${}9$ markierten Feld durch einen Pferdsprung verbunden. Also sind alle Felder zueinander äquivalent und es gibt nur eine Äquivalenzklasse.

This article is issued from Wikiversity. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.