Definiere die folgenden (kursiv gedruckten) Begriffe.

1. Eine Gruppe.
2. Die Eigenschaft, dass eine natürliche Zahl ${\displaystyle {}a}$ eine natürliche Zahl ${\displaystyle {}b}$ teilt
3. Verband/Komplementär/Definition/Begriff
4. Ungerichteter Graph/Sterngraph/Definition/Begriff
5. Ungerichteter Graph/Blatt/Definition/Begriff
6. Ungerichteter Graph/Adjazenzmatrix/Definition/Begriff

Formuliere die folgenden Sätze.

1. Der Satz über die Lösbarkeit von Gleichungen in einer Gruppe ${\displaystyle {}G}$.
2. /Fakt/Name
3. /Fakt/Name

Die Hochschule „Tellerrand“ bietet lediglich ${\displaystyle {}4}$ Fächer an, nämlich Hethitologie, Assyriologie, Ägyptologie und Semitistik. Sie bietet lediglich ${\displaystyle {}2}$-Fächer-Bachelor an in beliebiger Fächerkombination. Wie viele Fächerkombinationen gibt es (es wird nicht zwischen Erst- und Zweitfach unterschieden)? Skizziere ein Mengendiagramm, das die Studentenschaft mit ihren Fächern widergibt. Die zu einem Fach gehörenden Studenten und Studentinnen sollen dabei durch ein zusammenhängendes Gebiet dargestellt werden.

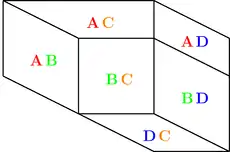
Es gibt ${\displaystyle {}6}$ Möglichkeiten.

Zeige, dass für natürliche Zahlen ${\displaystyle {}a,b,g}$ folgende Aussagen gelten.

1. Für teilerfremde ${\displaystyle {}a,b}$ ist

   ${\displaystyle {}\operatorname {kgV} \,(a,b)=ab\,.}$

2. Es gibt ${\displaystyle {}c,d\in \mathbb {Z} }$ mit

   ${\displaystyle a=c\cdot \operatorname {ggT} \,(a,b)\,\,{\text{ und }}\,\,b=d\cdot \operatorname {ggT} \,(a,b),}$

   wobei ${\displaystyle {}c,d}$ teilerfremd sind.

3. Es ist

   ${\displaystyle {}\operatorname {kgV} \,(ga,gb)=g\cdot \operatorname {kgV} \,(a,b)\,.}$

4. Es ist

   ${\displaystyle {}\operatorname {ggT} \,(a,b)\cdot \operatorname {kgV} \,(a,b)=ab\,.}$

1. Zunächst ist natürlich das Produkt ${\displaystyle {}ab}$ ein gemeinsames Vielfaches von ${\displaystyle {}a}$ und ${\displaystyle {}b}$. Sei also ${\displaystyle {}f}$ irgendein gemeinsames Vielfaches, also ${\displaystyle {}f=ua}$ und ${\displaystyle {}f=vb}$. Nach Fakt ***** gibt es im teilerfremden Fall Zahlen ${\displaystyle {}r,s\in \mathbb {Z} }$ mit ${\displaystyle {}ra+sb=1}$. Daher ist

   ${\displaystyle {}f=f\cdot 1=f(ra+sb)=fra+fsb=vbra+uasb=(vr+us)ab\,}$

   ein Vielfaches von ${\displaystyle {}ab}$.

2. Die Existenz von ${\displaystyle {}c}$ und ${\displaystyle {}d}$ ist klar. Hätten ${\displaystyle {}c}$ und ${\displaystyle {}d}$ einen gemeinsamen Teiler ${\displaystyle {}e\neq 1,-1}$, so ergäbe sich sofort der Widerspruch, dass ${\displaystyle {}e\cdot \operatorname {ggT} \,(a,b)}$ ein größerer gemeinsamer Teiler wäre.
3. Die rechte Seite ist offenbar ein gemeinsames Vielfaches von ${\displaystyle {}ga}$ und ${\displaystyle {}gb}$. Sei ${\displaystyle {}n}$ ein Vielfaches der linken Seite, also ein gemeinsames Vielfaches von ${\displaystyle {}ga}$ und ${\displaystyle {}gb}$. Dann kann man ${\displaystyle {}n=uga}$ und ${\displaystyle {}n=vgb}$ schreiben. Damit ist ${\displaystyle {}uga=vgb}$ und somit ist ${\displaystyle {}k:=ua=vb}$ (bei ${\displaystyle {}g\neq 0}$; bei ${\displaystyle {}g=0}$ ist die Behauptung direkt klar) ein gemeinsames Vielfaches von ${\displaystyle {}a}$ und ${\displaystyle {}b}$. Also ist ${\displaystyle {}n=gk}$ ein Vielfaches der rechten Seite.
4. Wir schreiben unter Verwendung der ersten Teile

   ${\displaystyle {}{\begin{aligned}\operatorname {ggT} \,(a,b)\cdot \operatorname {kgV} \,(a,b)&=\operatorname {ggT} \,(a,b)\cdot \operatorname {kgV} \,(c\cdot (\operatorname {ggT} \,(a,b)),d\cdot (\operatorname {ggT} \,(a,b)))\\&=\operatorname {ggT} \,(a,b)\cdot \operatorname {ggT} \,(a,b)\cdot \operatorname {kgV} \,(c,d)\\&=\operatorname {ggT} \,(a,b)\cdot \operatorname {ggT} \,(a,b)\cdot cd\\&=c\cdot \operatorname {ggT} \,(a,b)\cdot d\cdot \operatorname {ggT} \,(a,b)\\&=ab.\end{aligned}}}$