< Ebene algebraische Kurve < x^2-y^2+y^3 < Beschreibung
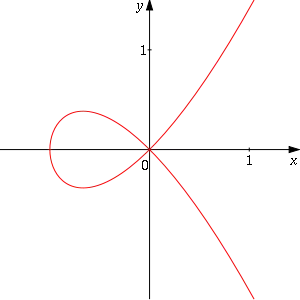
Wir betrachten die durch
gegebene Abbildung
Für die beiden Punkte ergibt sich der Wert . Für alle anderen Stellen kann man
schreiben. D.h. dass aus den Bildwerten rekonstruierbar ist, und das bedeutet, dass die Abbildung dort injektiv ist. Die Bildkurve ist also eine Kurve, die sich an genau einer Stelle überschneidet.
Wir bestimmen die Kurvengleichung, und schreiben und . Es ist und
Das beschreibende Polynom ist also
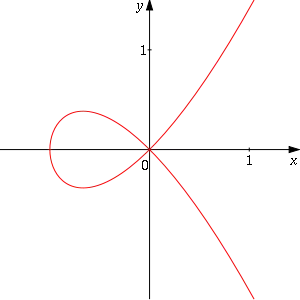
This article is issued from Wikiversity. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.