Wir betrachten die binomiale Gleichung ${\displaystyle {}X_{1}\cdots X_{n}=1}$. Die Nullstellenmenge ${\displaystyle {}V=V(X_{1}\cdots X_{n}-1)}$ besteht aus sämtlichen Punkten, deren Produkt der Koordinaten gleich ${\displaystyle {}1}$ ist. Insbesondere darf kein Eintrag gleich ${\displaystyle {}0}$ sein. Die Jacobimatrix ist

${\displaystyle \left(X_{2}\cdots X_{n},\,X_{1}X_{3}\cdots X_{n},\,\ldots ,\,X_{1}\cdots X_{n-2}X_{n},\,X_{1}\cdots X_{n-1}\right)}$

und diese besitzt in jedem Punkt der Nullstellenmenge den Rang ${\displaystyle {}1}$, es liegt also eine glatte Varietät vor. Der Satz über implizite Abbildungen liefert lokal die Existenz eines Diffeomorphismus zu ${\displaystyle {}K^{n-1}}$ (bei ${\displaystyle {}K=\mathbb {R} }$ oder ${\displaystyle {}\mathbb {C} }$), doch gibt es hier unmittelbar die bijektive algebraische (rationale) Abbildung

${\displaystyle {\left(K^{\times }\right)}^{n-1}\longrightarrow V,\,\left(x_{1},\,\ldots ,\,x_{n-1}\right)\longmapsto \left(x_{1},\,\ldots ,\,x_{n-1},\,{\frac {1}{x_{1}\cdots x_{n-1}}}\right).}$

Dies kann man so verstehen, dass ${\displaystyle {}V}$ der Graph zur rationalen Funktion auf ${\displaystyle {}{\left(K^{\times }\right)}^{n-1}}$ ist. Es liegt hier also ein Isomorphismus zwischen der Zariski-offenen Menge

${\displaystyle {}{\left(K^{\times }\right)}^{n-1}=K^{n-1}\setminus V(X_{1}\cdots X_{n-1})\subseteq K^{n-1}\,}$

und der Zariski-abgeschlossenen Menge ${\displaystyle {}V\subseteq K^{n}}$ vor. Die Menge ${\displaystyle {}{\left(K^{\times }\right)}^{n-1}}$ nennt man auch den ${\displaystyle {}(n-1)}$-dimensionalen Torus.

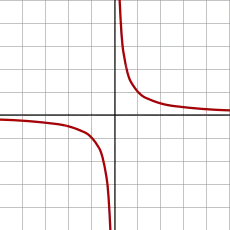
Bei ${\displaystyle {}n=2}$ ist das der Isomorphismus zwischen der punktierten Geraden und der Hyperbel.