Parabolische Koordinaten

Parabolische Koordinaten bilden ein Orthogonales Koordinatensystem, dessen Niveaulinien einen parabelförmigen Verlauf haben, siehe Bild. Die Parabeln haben alle denselben, im Ursprung liegenden Brennpunkt und heißen daher konfokal. Parabolische Koordinaten erlauben immer eine Trennung der Veränderlichen in der Laplace- und Helmholtz-Gleichung.[1]^:8 Anwendung finden diese Koordinaten beispielsweise beim Stark-Effekt.

Koordinatennetz der parabolischen Koordinaten in der Ebene. Der gemeinsame Brennpunkt aller Parabeln liegt auf der senkrechten Symmetrieachse in der Mitte des Bildes.

Durch Extrusion senkrecht zur xy-Ebene (in z-Richtung) entstehen parabolische Zylinderkoordinaten (englisch parabolic-cylinder coordinates[1]^:21,) und die Drehung um die im Bild senkrecht liegende Symmetrieachse liefert die ursprünglichen räumlichen parabolischen Koordinaten (englisch parabolic-coordinates[1]^:34.)

Zur Lösung der Gleichungen in parabolischen Zylinderkoordinaten wurden spezielle parabolische Zylinderfunktionen definiert.[2]^:138[3]

Ebene parabolische Koordinaten

In der xy-Ebene des Bildes oben gilt mit parabolischen Koordinaten $\mu ,\nu \in \mathbb {R} ,\,\mu \geq 0$

${\begin{pmatrix}x\\y\end{pmatrix}}={\begin{pmatrix}\mu \nu \\{\frac {1}{2}}(\nu ^{2}-\mu ^{2})\end{pmatrix}},\quad {\begin{pmatrix}\mu \\\nu \end{pmatrix}}={\begin{pmatrix}{\sqrt {{\sqrt {x^{2}+y^{2}}}-y}}\\{\rm {sign}}(x)\left({\sqrt {y^{2}+x^{2}}}+y\right)\end{pmatrix}}$

wo sign das Vorzeichen seines Arguments ausgibt. Die Kurven, auf denen μ konstant ist (was die Niveaulinien von μ in der xy-Ebene sind,) bilden die nach oben (d. h. in positiver y-Richtung) offenen konfokalen Parabeln

y=-{\frac {\mu ^{2}}{2}}+{\frac {x^{2}}{2\mu ^{2}}}

grün im Bild, während die Niveaulinien von ν nach unten offene konfokale Parabeln sind:

y={\frac {\nu ^{2}}{2}}-{\frac {x^{2}}{2\nu ^{2}}}

rot im Bild. Fasst man die Ebene als komplexe Ebene auf mit imaginärer Einheit i²=-1, so gilt

x+{\rm {i}}y=-{\frac {\rm {i}}{2}}(\mu +{\rm {i}}\nu )^{2}.

Die Potenzierung komplexer Zahlen mit reellem Exponenten ist eine Holomorphe Funktion, was die Orthogonalität der parabolischen Koordinaten in der Ebene begründet.

Metrische Faktoren, Weg- und Flächenelemente in der Ebene

Die kovarianten Basisvektoren sind

{\vec {g}}_{\mu }={\frac {\partial }{\partial \mu }}{\begin{pmatrix}x\\y\end{pmatrix}}={\begin{pmatrix}\nu \\-\mu \end{pmatrix}},\quad {\vec {g}}_{\nu }={\frac {\partial }{\partial \nu }}{\begin{pmatrix}x\\y\end{pmatrix}}={\begin{pmatrix}\mu \\\nu \end{pmatrix}}

die, wie es sein muss, senkrecht zueinander sind, und deren Beträge die metrischen Faktoren sind:

h_{\mu }:=|{\vec {g}}_{\mu }|={\sqrt {\mu ^{2}+\nu ^{2}}},\quad h_{\nu }:=|{\vec {g}}_{\nu }|={\sqrt {\mu ^{2}+\nu ^{2}}}=h_{\mu }:=h

Das parabolische Orthonormalsystem ist dementsprechend

{\hat {c}}_{\mu }={\frac {1}{h}}{\begin{pmatrix}\nu \\-\mu \end{pmatrix}},\quad {\hat {c}}_{\nu }={\frac {1}{h}}{\begin{pmatrix}\mu \\\nu \end{pmatrix}}

Das Linien- und Flächenelement ergibt sich zu

{\begin{aligned}{\rm {d}}{\vec {r}}=&{\vec {g}}_{\mu }{\rm {d}}\mu +{\vec {g}}_{\nu }{\rm {d}}\nu \\{\rm {d}}s^{2}:=&|{\rm {d}}{\vec {r}}|^{2}=h^{2}({\rm {d}}\mu ^{2}+{\rm {d}}\nu ^{2})\\{\rm {d}}A:=&h^{2}{\rm {d}}\mu \,{\rm {d}}\nu \end{aligned}}

Operatoren in der Ebene

Die üblichen Differentialoperatoren führt die Tabelle auf[1]^:21 $(h={\sqrt {\mu ^{2}+\nu ^{2}}},{\vec {v}}=v_{\mu }{\hat {c}}_{\mu }+v_{\nu }{\hat {c}}_{\nu })$

Gradient	${\rm {grad}}\,f={\frac {1}{h}}\left({\hat {c}}_{\mu }{\frac {\partial f}{\partial \mu }}+{\hat {c}}_{\nu }{\frac {\partial f}{\partial \nu }}\right)$
Divergenz	${\rm {div}}\,{\vec {v}}={\frac {1}{h^{2}}}\left({\frac {\partial (hv_{\mu })}{\partial \mu }}+{\frac {\partial (hv_{\nu })}{\partial \nu }}\right)$
Rotation	${\rm {rot}}\,{\vec {v}}={\frac {1}{h^{2}}}\left({\frac {\partial (hv_{\nu })}{\partial \mu }}-{\frac {\partial (hv_{\mu })}{\partial \nu }}\right)$
Laplace-Operator	$\Delta f={\frac {1}{h^{2}}}\left({\frac {\partial ^{2}f}{\partial \mu ^{2}}}+{\frac {\partial ^{2}f}{\partial \nu ^{2}}}\right)$

Lösung der Laplace- und Helmholtz-Gleichung in der Ebene

Die besondere Form des Laplace-Operators erlaubt eine Lösung der Helmholtz-Gleichung durch multiplikative Trennung der Veränderlichen gemäß dem Separationsansatz[1]^:22

\phi (\mu ,\nu )=M(\mu )\cdot N(\nu )

Mit obigem Laplace-Operator entsteht die Helmholtz-Gleichung:

\Delta \phi (\mu ,\nu )={\frac {1}{\mu ^{2}+\nu ^{2}}}\left({\frac {{\rm {d}}^{2}M}{{\rm {d}}\mu ^{2}}}N+M{\frac {{\rm {d}}^{2}N}{{\rm {d}}\nu ^{2}}}\right)=\lambda \cdot M\cdot N

Multiplikation beider Seiten mit ${\tfrac {\mu ^{2}+\nu ^{2}}{M\cdot N}}$ liefert umgestellt

{\frac {\frac {{\rm {d}}^{2}M}{{\rm {d}}\mu ^{2}}}{M}}-\lambda \mu ^{2}=\lambda \nu ^{2}-{\frac {\frac {{\rm {d}}^{2}N}{{\rm {d}}\nu ^{2}}}{N}}

Weil die linke Seite nur von μ und die rechte nur von ν abhängt, stehen auf beiden Seiten Konstanten:

{\begin{aligned}{\frac {\frac {{\rm {d}}^{2}M}{{\rm {d}}\mu ^{2}}}{M}}-\lambda \mu ^{2}=\kappa ^{2}\rightarrow {\frac {{\rm {d}}^{2}M}{{\rm {d}}\mu ^{2}}}-(\lambda \mu ^{2}+\kappa ^{2})M=0\\\lambda \nu ^{2}-{\frac {\frac {{\rm {d}}^{2}N}{{\rm {d}}\nu ^{2}}}{N}}=\kappa ^{2}\rightarrow {\frac {{\rm {d}}^{2}N}{{\rm {d}}\nu ^{2}}}-(\lambda \nu ^{2}-\kappa ^{2})N=0\end{aligned}}

Rechts stehen Webersche Differentialgleichungen[4], die von parabolischen Zylinderfunktionen erfüllt werden.[2]^:138[3].

Im Fall der Laplace-Gleichung ist λ=0 und die Lösungsfunktion kann mit dem Sinus und Cosinus sowie dem Sinus hyperbolicus und Kosinus hyperbolicus ausgedrückt werden:

\phi (\mu ,\nu )=[A\sinh(\kappa \mu )+B\cosh(\kappa \mu )][C\sin(\kappa \nu )+D\cos(\kappa \nu )]

Die Konstanten A, B, C, D und κ dienen der Anpassung an Randbedingungen. Wenn die Separationskonstante κ² mit negativem Vorzeichen angesetzt wird, vertauschen sich in der Lösungsfunktion die Winkelfunktionen durch die Hyperbelfunktionen und umgekehrt.

Parabolische Koordinaten im Raum

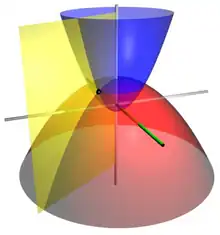
Koordinatenflächen der (räumlichen) parabolischen Koordinaten. Das rote Paraboloid entspricht μ=2, das blaue ν=1 und die gelbe Halbebene ψ=−60°.

Durch Rotation der Parabeln um ihre Symmetrieachse entstehen (räumliche) parabolische Koordinaten, siehe Bild.[1]^:34 Für eine ein-eindeutige Beziehung zwischen den Kartesischen Koordinaten und den parabolischen Koordinaten wird nur die rechte Halbebene gedreht, sodass mit den Einschränkungen $\mu ,\nu ,\psi \in \mathbb {R} ^{\geq 0},\psi <2\pi$ die Zusammenhänge

{\begin{aligned}&{\vec {r}}(\mu ,\nu ,\psi )={\begin{pmatrix}x\\y\\z\end{pmatrix}}={\begin{pmatrix}\mu \nu \cos \psi \\\mu \nu \sin \psi \\{\frac {1}{2}}(\mu ^{2}-\nu ^{2})\end{pmatrix}}\\&{\begin{pmatrix}\mu \\\nu \\\psi \end{pmatrix}}={\begin{pmatrix}{\sqrt {r+z}}\\{\sqrt {r-z}}\\{\rm {atan2}}(y,x)\end{pmatrix}},\;r={\sqrt {x^{2}+y^{2}+z^{2}}}\end{aligned}}

ein-eindeutig sind. Darin ist atan2 eine Umkehrfunktion des Tangens.

Metrische Faktoren, Weg- und Flächenelemente im Raum

Die kovarianten Basisvektoren sind

g_{\mu }={\frac {\partial {\vec {r}}}{\partial \mu }}={\begin{pmatrix}\nu \cos(\psi )\\\nu \sin(\psi )\\\mu \end{pmatrix}},\;g_{\nu }={\frac {\partial {\vec {r}}}{\partial \nu }}={\begin{pmatrix}\mu \cos(\psi )\\\mu \sin(\psi )\\-\nu \end{pmatrix}},\;g_{\psi }={\frac {\partial {\vec {r}}}{\partial \psi }}={\begin{pmatrix}-\mu \nu \sin(\psi )\\\mu \nu \cos(\psi )\\0\end{pmatrix}}

aus denen sich die metrischen Faktoren

h_{\mu }:=|{\vec {g}}_{\mu }|=h_{\nu }:=|{\vec {g}}_{\nu }|=:h={\sqrt {\mu ^{2}+\nu ^{2}}},\quad h_{\psi }:=|{\vec {g}}_{\psi }|=\mu \nu

ergeben. Das parabolische Orthonormalsystem ist demzufolge

{\hat {c}}_{\mu }={\frac {1}{h}}{\begin{pmatrix}\nu \cos(\psi )\\\nu \sin(\psi )\\\mu \end{pmatrix}},\quad {\hat {c}}_{\nu }={\frac {1}{h}}{\begin{pmatrix}\mu \cos(\psi )\\\mu \sin(\psi )\\-\nu \end{pmatrix}},\quad {\hat {c}}_{\psi }={\begin{pmatrix}-\sin(\psi )\\\cos(\psi )\\0\end{pmatrix}}

Die Linien-, Flächen- und Volumenelemente ergeben sich zu

{\begin{aligned}{\rm {d}}{\vec {r}}=&{\vec {g}}_{\mu }\,{\rm {d}}\mu +{\vec {g}}_{\nu }\,{\rm {d}}\nu +{\vec {g}}_{\psi }\,{\rm {d}}\psi \\{\rm {d}}s^{2}:=&|{\rm {d}}{\vec {r}}|^{2}=h^{2}({\rm {d}}\mu ^{2}+{\rm {d}}\nu ^{2})+\mu ^{2}\nu ^{2}\,{\rm {d}}\psi ^{2}\\\mathrm {d} {\vec {a}}=&+h^{2}{\hat {c}}_{\psi }\,\mathrm {d} \mu \,\mathrm {d} \nu +h\mu \nu {\hat {c}}_{\mu }\,\mathrm {d} \nu \,\mathrm {d} \psi +h\mu \nu {\hat {c}}_{\nu }\,\mathrm {d} \psi \,\mathrm {d} \mu \\\mathrm {d} V=&h^{2}\mu \nu \,\mathrm {d} \mu \,\mathrm {d} \nu \,\mathrm {d} \psi \end{aligned}}

Operatoren im Raum

Die üblichen Differentialoperatoren führt die Tabelle auf[1]^:35 $(h={\sqrt {\mu ^{2}+\nu ^{2}}},{\vec {v}}=v_{\mu }{\hat {c}}_{\mu }+v_{\nu }{\hat {c}}_{\nu }+v_{\psi }{\hat {c}}_{\psi })$

Gradient	${\rm {grad}}\,f={\frac {1}{h}}\left({\hat {c}}_{\mu }{\frac {\partial f}{\partial \mu }}+{\hat {c}}_{\nu }{\frac {\partial f}{\partial \nu }}\right)+{\frac {{\hat {c}}_{\psi }}{\mu \nu }}{\frac {\partial f}{\partial \psi }}$
Divergenz	${\rm {div}}\,{\vec {v}}={\frac {1}{h^{2}}}\left({\frac {1}{\mu }}{\frac {\partial (h\mu v_{\mu })}{\partial \mu }}+{\frac {1}{\nu }}{\frac {\partial (h\nu v_{\nu })}{\partial \nu }}\right)+{\frac {1}{\mu \nu }}{\frac {\partial v_{\psi }}{\partial \psi }}$
Rotation	${\rm {rot}}\,{\vec {v}}={\frac {{\hat {c}}_{\mu }}{h\mu \nu }}\left[{\frac {\partial (\mu \nu v_{\psi })}{\partial \nu }}-{\frac {\partial (hv_{\nu })}{\partial \psi }}\right]+{\frac {{\hat {c}}_{\nu }}{h\mu \nu }}\left[{\frac {\partial (hv_{\mu })}{\partial \psi }}-{\frac {\partial (\mu \nu v_{\psi })}{\partial \mu }}\right]+{\frac {{\hat {c}}_{\psi }}{h^{2}}}\left[{\frac {\partial (hv_{\nu })}{\partial \mu }}-{\frac {\partial (hv_{\mu })}{\partial \nu }}\right]$
Laplace-Operator	$\Delta f={\frac {1}{h^{2}}}\left[{\frac {\partial ^{2}f}{\partial \mu ^{2}}}+{\frac {1}{\mu }}{\frac {\partial f}{\partial \mu }}+{\frac {1}{\nu }}{\frac {\partial f}{\partial \nu }}+{\frac {\partial ^{2}f}{\partial \nu ^{2}}}\right]+{\frac {1}{\mu ^{2}\nu ^{2}}}{\frac {\partial ^{2}f}{\partial \psi ^{2}}}$

Lösung der Laplace- und Helmholtz-Gleichung im Raum

Die Helmholtz-Gleichung $\Delta \phi =\lambda \phi$ schreibt sich mit obigem Laplace-Operator:

{\frac {1}{\mu ^{2}+\nu ^{2}}}\left[{\frac {\partial ^{2}\phi }{\partial \mu ^{2}}}+{\frac {1}{\mu }}{\frac {\partial \phi }{\partial \mu }}+{\frac {1}{\nu }}{\frac {\partial \phi }{\partial \nu }}+{\frac {\partial ^{2}\phi }{\partial \nu ^{2}}}\right]+{\frac {1}{\mu ^{2}\nu ^{2}}}{\frac {\partial ^{2}\phi }{\partial \psi ^{2}}}=\lambda \phi

Mit dem Separationsansatz[1]^:36

\phi (\mu ,\nu ,\psi )=M(\mu )\cdot N(\nu )\cdot \Psi (\psi )

liefert Multiplikation der Helmholtz-Gleichung mit ${\tfrac {\mu ^{2}\nu ^{2}}{MN\Psi }}$

{\frac {\mu ^{2}\nu ^{2}}{\mu ^{2}+\nu ^{2}}}\left[{\frac {\frac {{\rm {d}}^{2}M}{{\rm {d}}\mu ^{2}}}{M}}+{\frac {\frac {{\rm {d}}M}{{\rm {d}}\mu }}{\mu M}}+{\frac {\frac {{\rm {d}}N}{{\rm {d}}\nu }}{\nu N}}+{\frac {\frac {{\rm {d}}^{2}N}{{\rm {d}}\nu ^{2}}}{N}}\right]+{\frac {\frac {{\rm {d}}^{2}\Psi }{{\rm {d}}\psi ^{2}}}{\Psi }}=\lambda \mu ^{2}\nu ^{2}

Nur der letzte Bruch auf der linken Seite hängt von ψ ab, weswegen er eine Konstante κ darstellt:

{\frac {\frac {{\rm {d}}^{2}\Psi }{{\rm {d}}\psi ^{2}}}{\Psi }}=\kappa

Einsetzen von κ gestattet auch μ und ν voneinander zu trennen:

{\frac {\frac {{\rm {d}}^{2}M}{{\rm {d}}\mu ^{2}}}{M}}+{\frac {\frac {{\rm {d}}M}{{\rm {d}}\mu }}{\mu M}}+{\frac {\kappa }{\mu ^{2}}}-\lambda \mu ^{2}=\lambda \nu ^{2}-{\frac {\kappa }{\nu ^{2}}}-{\frac {\frac {{\rm {d}}N}{{\rm {d}}\nu }}{\nu N}}-{\frac {\frac {{\rm {d}}^{2}N}{{\rm {d}}\nu ^{2}}}{N}}

Weil die linke Seite nur von μ und die rechte nur von ν abhängen, können beide Seiten der Gleichung mit einer Konstanten η gleichgesetzt werden, was auf die Differentialgleichungen

{\begin{aligned}{\frac {\mathrm {d} ^{2}M}{\mathrm {d} \mu ^{2}}}+{\frac {1}{\mu }}{\frac {\mathrm {d} M}{\mathrm {d} \mu }}+\left({\frac {\kappa }{\mu ^{2}}}-\eta -\lambda \mu ^{2}\right)M=&0\\{\frac {\mathrm {d} ^{2}N}{\mathrm {d} \nu ^{2}}}+{\frac {1}{\nu }}{\frac {\mathrm {d} N}{\mathrm {d} \nu }}+\left({\frac {\kappa }{\nu ^{2}}}+\eta -\lambda \nu ^{2}\right)N=&0\\{\frac {\mathrm {d} ^{2}\Psi }{\mathrm {d} \psi ^{2}}}-\kappa \Psi =&0\end{aligned}}

führt, für die es Lösungen gibt.[1]^:36

Parabolische Zylinderkoordinaten

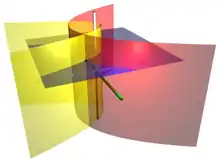
Koordinatenflächen der parabolischen Zylinderkoordinaten. Der rote parabolische Zylinder entspricht μ=2, der gelbe ν=1 und die blaue Ebene z=2.

Die parabolischen Zylinderkoordinaten entstehen aus den ebenen parabolischen Koordinaten des vorangegangenen Abschnitts durch Extrusion senkrecht zur xy-Ebene in z-Richtung, sodass viele Eigenschaften von dort hierher übertragen werden können.

Die parabolischen Zylinderkoordinaten $(\mu ,\nu ,z)$ und die kartesischen $(x,y,z)$ hängen wie folgt zusammen:

${\begin{pmatrix}x\\y\\z\end{pmatrix}}={\begin{pmatrix}\mu \nu \\{\frac {1}{2}}(\nu ^{2}-\mu ^{2})\\z\end{pmatrix}},\quad {\begin{pmatrix}\mu \\\nu \\z\end{pmatrix}}={\begin{pmatrix}{\sqrt {{\sqrt {x^{2}+y^{2}}}-y}}\\{\rm {sign}}(x)\left({\sqrt {y^{2}+x^{2}}}+y\right)\\z\end{pmatrix}}$

Die Niveauflächen, auf denen μ konstant ist, sind in positiver y-Richtung offene konfokale parabolische Zylinder[2]^:140 mit

y=-{\frac {\mu ^{2}}{2}}+{\frac {x^{2}}{2\mu ^{2}}}

rot im Bild, während die Niveauflächen von ν die in negativer y-Richtung offenen konfokalen parabolischen Zylinder sind:

y={\frac {\nu ^{2}}{2}}-{\frac {x^{2}}{2\nu ^{2}}}

gelb im Bild. Die Niveauflächen mit z=const. sind zueinander parallele Ebenen, blau im Bild.

Metrische Faktoren, Weg- und Flächenelemente in parabolischen Zylinderkoordinaten

Die Kovarianten Basisvektoren sind

{\vec {g}}_{\mu }={\frac {\partial }{\partial \mu }}{\begin{pmatrix}x\\y\\z\end{pmatrix}}={\begin{pmatrix}\nu \\-\mu \\0\end{pmatrix}},\quad {\vec {g}}_{\nu }={\frac {\partial }{\partial \nu }}{\begin{pmatrix}x\\y\\z\end{pmatrix}}={\begin{pmatrix}\mu \\\nu \\0\end{pmatrix}},\quad {\vec {g}}_{z}={\frac {\partial }{\partial z}}{\begin{pmatrix}x\\y\\z\end{pmatrix}}={\begin{pmatrix}0\\0\\1\end{pmatrix}}

die, wie es sein muss, senkrecht zueinander sind, und deren Beträge die metrischen Faktoren sind:

h_{\mu }:=|{\vec {g}}_{\mu }|={\sqrt {\mu ^{2}+\nu ^{2}}},\quad h_{\nu }:=|{\vec {g}}_{\nu }|={\sqrt {\mu ^{2}+\nu ^{2}}}=h_{\mu }:=h,\quad h_{z}:=|{\vec {g}}_{z}|=1

Das parabolische zylindrische Orthonormalsystem ist dementsprechend

{\hat {c}}_{\mu }={\frac {1}{h}}{\begin{pmatrix}\nu \\-\mu \\0\end{pmatrix}},\quad {\hat {c}}_{\nu }={\frac {1}{h}}{\begin{pmatrix}\mu \\\nu \\0\end{pmatrix}},\quad {\hat {c}}_{z}={\begin{pmatrix}0\\0\\1\end{pmatrix}}

Das Linien-, Flächen- und Volumenelement lauten

{\begin{aligned}{\rm {d}}{\vec {r}}=&h{\hat {c}}_{\mu }\,{\rm {d}}\mu +h{\hat {c}}_{\nu }\,{\rm {d}}\nu +{\hat {c}}_{z}\,{\rm {d}}z\\{\rm {d}}s^{2}:=&|{\rm {d}}{\vec {r}}|^{2}=h^{2}({\rm {d}}\mu ^{2}+{\rm {d}}\nu ^{2})+{\rm {d}}z^{2}\\{\rm {d}}A:=&h{\hat {c}}_{\nu }\,{\rm {d}}\mu \,\,{\rm {d}}z+h{\hat {c}}_{\mu }\,{\rm {d}}\nu \,{\rm {d}}z+h^{2}{\hat {c}}_{z}\,{\rm {d}}\nu \,{\rm {d}}\mu \\{\rm {d}}V:=&h^{2}{\rm {d}}\mu \,{\rm {d}}\nu \,{\rm {d}}z\end{aligned}}

Operatoren in parabolischen Zylinderkoordinaten

Die üblichen Differentialoperatoren führt die Tabelle auf[1]^:21 $(h={\sqrt {\mu ^{2}+\nu ^{2}}},{\vec {v}}=v_{\mu }{\hat {c}}_{\mu }+v_{\nu }{\hat {c}}_{\nu }+v_{z}{\hat {c}}_{z})$

Gradient	${\rm {grad}}\,f={\frac {1}{h}}\left({\hat {c}}_{\mu }{\frac {\partial f}{\partial \mu }}+{\hat {c}}_{\nu }{\frac {\partial f}{\partial \nu }}\right)+{\hat {c}}_{z}{\frac {\partial f}{\partial z}}$
Divergenz	${\rm {div}}\,{\vec {v}}={\frac {1}{h^{2}}}\left({\frac {\partial (hv_{\mu })}{\partial \mu }}+{\frac {\partial (hv_{\nu })}{\partial \nu }}\right)+{\frac {\partial v_{z}}{\partial z}}$
Rotation	${\rm {rot}}\,{\vec {v}}={\frac {{\hat {c}}_{\mu }}{h}}\left[{\frac {\partial v_{z}}{\partial \nu }}-{\frac {\partial (hv_{\nu })}{\partial z}}\right]+{\frac {{\hat {c}}_{\nu }}{h}}\left[{\frac {\partial (hv_{\mu })}{\partial z}}-{\frac {\partial v_{z}}{\partial \mu }}\right]+{\frac {{\hat {c}}_{z}}{h^{2}}}\left[{\frac {\partial (hv_{\nu })}{\partial \mu }}-{\frac {\partial (hv_{\mu })}{\partial \nu }}\right]$
Laplace-Operator	$\Delta f={\frac {1}{h^{2}}}\left({\frac {\partial ^{2}f}{\partial \mu ^{2}}}+{\frac {\partial ^{2}f}{\partial \nu ^{2}}}\right)+{\frac {\partial ^{2}f}{\partial z^{2}}}$

Lösung der Laplace- und Helmholtz-Gleichung in parabolischen Zylinderkoordinaten

Die multiplikative Trennung der Veränderlichen verläuft ähnlich wie bei der #Lösung der Laplace- und Helmholtz-Gleichung in der Ebene, es muss nur die z-Koordinate hinzugenommen werden[1]^:22

\phi (\mu ,\nu )=M(\mu )\cdot N(\nu )\cdot Z(z)

Mit obigem Laplace-Operator entsteht die Helmholtz-Gleichung:

\Delta \phi (\mu ,\nu )={\frac {1}{\mu ^{2}+\nu ^{2}}}\left({\frac {{\rm {d}}^{2}M}{{\rm {d}}\mu ^{2}}}NZ+M{\frac {{\rm {d}}^{2}N}{{\rm {d}}\nu ^{2}}}Z\right)+MN{\frac {{\rm {d}}^{2}Z}{{\rm {d}}z^{2}}}=\lambda MNZ

Division beider Seiten durch $MNZ$ liefert

{\frac {1}{\mu ^{2}+\nu ^{2}}}\left({\frac {\frac {{\rm {d}}^{2}M}{{\rm {d}}\mu ^{2}}}{M}}+{\frac {\frac {{\rm {d}}^{2}N}{{\rm {d}}\nu ^{2}}}{N}}\right)+{\frac {\frac {{\rm {d}}^{2}Z}{{\rm {d}}z^{2}}}{Z}}=\lambda

Auf der rechten Seite steht eine Konstante und nur der letzte Bruch auf der linken Seite hängt von z ab. Daher muss dieser Term ebenfalls konstant sein:

{\frac {\frac {{\rm {d}}^{2}Z}{{\rm {d}}z^{2}}}{Z}}:=\eta \rightarrow Z(z)=E\exp({\sqrt {\eta }}z)+F\exp(-{\sqrt {\eta }}z)

Diese Konstante oben eingesetzt ergibt wie in der Ebene nur mit λ-η statt λ:

{\begin{aligned}{\frac {{\rm {d}}^{2}M}{{\rm {d}}\mu ^{2}}}-[(\lambda -\eta )\mu ^{2}+\kappa ^{2}]M=0\\{\frac {{\rm {d}}^{2}N}{{\rm {d}}\nu ^{2}}}-[(\lambda -\eta )\nu ^{2}-\kappa ^{2}]N=0\end{aligned}}

und die Lösung erfolgt auch wie dort.

Im Fall der Laplace-Gleichung ist λ=0 und die Lösungsfunktion kann mit dem Sinus und Cosinus sowie dem Sinus hyperbolicus und Kosinus hyperbolicus ausgedrückt werden:

\phi (\mu ,\nu ,z)=[A\sinh(\kappa \mu )+B\cosh(\kappa \mu )][C\sin(\kappa \nu )+D\cos(\kappa \nu )][E\exp({\sqrt {\eta }}z)+F\exp(-{\sqrt {\eta }}z)]

Die Konstanten A, B, C, D, E, F, η und κ dienen der Anpassung an Randbedingungen. Wenn die Separationskonstante κ² mit negativem Vorzeichen angesetzt wird, vertauschen sich in der Lösungsfunktion die Winkelfunktionen durch die Hyperbelfunktionen und umgekehrt, und je nach Vorzeichen von η ist der von z abhängige Faktor eine Wellen- oder Exponentialfunktion.

Literatur

P. Moon, D.E. Spencer: Field Theory Handbook. Including Coordinate Systems, Differential Equations and Their Solutions. 2. Auflage. Springer Verlag, Berlin, Heidelberg, New York 1971, ISBN 3-540-02732-7, S. 3 ff.
Guido Walz (Hrsg.): Lexikon der Mathematik. 2. Auflage. Band 4 (Moo bis Sch). Springer Spektrum Verlag, Mannheim 2017, ISBN 978-3-662-53499-1, doi:10.1007/978-3-662-53500-4.
Eric Weisstein: Parabolic Cylinder Function. MathWorld, 16. April 2024, abgerufen am 13. April 2024 (englisch).
Guido Walz (Hrsg.): Lexikon der Mathematik. 2. Auflage. Band 5 (Sed bis Zyl). Springer Spektrum Verlag, Mannheim 2017, ISBN 978-3-662-53505-9, doi:10.1007/978-3-662-53506-6.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[Spencer-1] P. Moon, D.E. Spencer: Field Theory Handbook. Including Coordinate Systems, Differential Equations and Their Solutions. 2. Auflage. Springer Verlag, Berlin, Heidelberg, New York 1971, ISBN 3-540-02732-7, S. 3 ff.

[MatheLexikon4-2] Guido Walz (Hrsg.): Lexikon der Mathematik. 2. Auflage. Band 4 (Moo bis Sch). Springer Spektrum Verlag, Mannheim 2017, ISBN 978-3-662-53499-1, doi:10.1007/978-3-662-53500-4.

[MathWorld-3] Eric Weisstein: Parabolic Cylinder Function. MathWorld, 16. April 2024, abgerufen am 13. April 2024 (englisch).

[MatheLexikon5-4] Guido Walz (Hrsg.): Lexikon der Mathematik. 2. Auflage. Band 5 (Sed bis Zyl). Springer Spektrum Verlag, Mannheim 2017, ISBN 978-3-662-53505-9, doi:10.1007/978-3-662-53506-6.