Serlo: EN: Geometric series

Geometric series are series of the form $\sum _{k=0}^{\infty }q^{k}$ . They are important within several proofs in real analysis. In particular, they are crucial for proving convergence or divergence of other series. We will derive some criteria using them, e.g. the ratio or the root criterion.

Geometric sum formula

We recall the geometric sum formula for partial sums of the geometric series. The proof of the sum formula reads as follows:

Theorem (Geometrische Summenformel)

For all real $q\neq 1$ and for all $n\in \mathbb {N} _{0}$ there is:

\sum _{k=0}^{n}q^{k}={\frac {1-q^{n+1}}{1-q}}

Proof (Geometrische Summenformel)

We have

{\begin{aligned}\sum _{k=0}^{n}q^{k}&=\ 1+q+q^{2}+\dotsb +q^{n}\\[0.5em]&{\color {OliveGreen}\left\downarrow \ {\text{multiply both side by }}q\right.}\\[0.5em]\implies \ q\cdot \sum _{k=0}^{n}q^{k}&=\ q+q^{2}+q^{3}+\dotsb +q^{n+1}\\[0.5em]&{\color {OliveGreen}\left\downarrow \ {\text{subtract second from first equation}}\right.}\\[0.5em]\implies \ \sum _{k=0}^{n}q^{k}-q\cdot \sum _{k=0}^{n}q^{k}&=\ (1+q+\dotsb +q^{n})-(q+q^{2}+\dotsb +q^{n+1})\\[0.5em]&=1-q^{n+1}\\[0.5em]&{\color {OliveGreen}\left\downarrow \ {\text{factor out }}\sum _{k=0}^{n}q^{k}\right.}\\[0.5em]\implies \ (1-q)\cdot \sum _{k=0}^{n}q^{k}&=\ 1-q^{n+1}\\[0.5em]&{\color {OliveGreen}\left\downarrow \ {}\cdot {\frac {1}{1-q}}{\text{, since }}q\neq 1\right.}\\[0.5em]\implies \ \sum _{k=0}^{n}q^{k}&=\ {\frac {1-q^{n+1}}{1-q}}\\[0.5em]\end{aligned}}

Geometric series

The geometric series

\sum _{k=0}^{\infty }r^{k}

converges for

r={\tfrac {1}{2}}

,

r={\tfrac {1}{3}}

or

r={\tfrac {1}{4}}

.

We consider two cases: $|q|<1$ and $|q|\geq 1$ .

Case $|q|<1$

We consider the geometric series $\sum _{k=0}^{\infty }q^{k}$ for any $|q|<1$ , which especially means $q\neq 1$ . The sum formula above applies to the partial sums in that case:

{\begin{aligned}\sum _{k=0}^{\infty }q^{k}&=\left(\sum _{k=0}^{n}q^{k}\right)_{n\in \mathbb {N} }\\[1em]&{\color {OliveGreen}\left\downarrow \ {\text{geometric sum formula }}(q\neq 1)\right.}\\[1em]&=\left({\frac {1-q^{n+1}}{1-q}}\right)_{n\in \mathbb {N} }\end{aligned}}

So the geometric series converges if and only if the sequence of partial sums $\left({\tfrac {1-q^{n+1}}{1-q}}\right)_{n\in \mathbb {N} }$ converges. This is the case if and only if $\left(q^{n}\right)_{n\in \mathbb {N} }$ converges. We know that $\left(q^{n}\right)_{n\in \mathbb {N} }$ converges to $0$ if and only if $|q|<1$ and it converges to $1$ , if and only if $q=1$ . In this section, we only care about the first case of convergence:

If $|q|<1$ , then the geometric series $\sum _{k=0}^{\infty }q^{k}$ converges.

Now, let us determine its limit:

{\begin{aligned}\sum _{k=0}^{\infty }q^{k}&=\lim _{n\to \infty }\sum _{k=0}^{n}q^{k}\\[0.3em]&=\lim _{n\to \infty }{\frac {1-q^{n+1}}{1-q}}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{limit theorems}}\right.}\\[0.3em]&={\frac {1-\lim _{n\to \infty }q^{n+1}}{1-q}}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ |q|<1\right.}\\[0.3em]&={\frac {1-0}{1-q}}\\[0.3em]&={\frac {1}{1-q}}\end{aligned}}

Exercise (alternative proof that the geometric series converges)

Prove that the geometric series $\sum _{k=0}^{\infty }q^{k}$ with $|q|<1$ converges to ${\tfrac {1}{1-q}}$ .

How to get to the proof? (alternative proof that the geometric series converges)

We need to show that for each $\epsilon >0$ there is an $N\in \mathbb {N}$ , such that

\left|\sum _{k=0}^{n}q^{k}-{\frac {1}{1-q}}\right|<\epsilon

for all

n\geq N

The geometric sum formula yields

\left|\sum _{k=0}^{n}q^{k}-{\frac {1}{1-q}}\right|=\left|{\frac {1-q^{n+1}}{1-q}}-{\frac {1}{1-q}}\right|=\left|{\frac {1-q^{n+1}-1}{1-q}}\right|=\left|{\frac {q^{n+1}}{1-q}}\right|={\frac {1}{1-q}}\cdot |q^{n+1}|

Since the geometric sequence $(q^{n})_{n\in \mathbb {N} }$ with $|q|<1$ converges to 0, so does $(q^{n+1})_{n\in \mathbb {N} }$ . Hence, for every ${\tilde {\epsilon }}>0$ there is an ${\tilde {N}}\in \mathbb {N}$ with

|q^{n+1}-0|<{\tilde {\epsilon }}

for all

n\geq {\tilde {N}}

Since ${\frac {1}{1-q}}$ is constant, there is an $N\in \mathbb {N}$ with

{\frac {1}{1-q}}\cdot |q^{n+1}|<\epsilon

for all

n\geq N

This implies the desired convergence.

Proof (alternative proof that the geometric series converges)

Let $\epsilon >0$ be given. The geometric sequence $(q^{n})_{n\in \mathbb {N} }$ with $|q|<1$ converges to 0. Since $|q|<1$ , for a given ${\tilde {\epsilon }}:=(1-q)\cdot \epsilon >0$ there is an $N\in \mathbb {N}$ with

|q^{n}|<{\tilde {\epsilon }}

for all

n\geq N

With the geometric sum formula, this implies for all $n\geq N$ that

{\begin{aligned}&\left|\sum _{k=0}^{n}q^{k}-{\frac {1}{1-q}}\right|=\left|{\frac {1-q^{n+1}}{1-q}}-{\frac {1}{1-q}}\right|\\[0.3em]=\ &{\frac {1}{1-q}}\cdot |q^{n+1}|\\[0.3em]&{\color {OliveGreen}\left\downarrow \ n+1\geq N\right.}\\[0.3em]<\ &{\frac {1}{1-q}}\cdot {\tilde {\epsilon }}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\tilde {\epsilon }}=(1-q)\cdot \epsilon \right.}\\[0.3em]=\ &{\frac {1}{1-q}}\cdot (1-q)\cdot \epsilon =\epsilon \end{aligned}}

The limit of the series is hence: $\sum _{k=0}^{\infty }q^{k}={\frac {1}{1-q}}$ .

Case $|q|\geq 1$

For $|q|\geq 1$ , we have for all $k\in \mathbb {N} _{0}$ , that $\left|q^{k}\right|\geq 1$ . Therefore, the sequence $\left(q^{k}\right)_{k\in \mathbb {N} _{0}}$ cannot converge to 0. So teh series $\sum _{k=0}^{\infty }q^{k}$ must diverge (this argument is called term test and will be considered in detail, later)

The divergence becomes particularly obvious, if $q$ is positive, e.g. for $q\geq 1$ . In this case, for all $k\in \mathbb {N}$ , we have $q^{k}\geq 1$ and may estimate the partial sums: $\sum _{k=1}^{n}q^{k}\geq \sum _{k=1}^{n}1=n$ So the sequence of partial sums is bounded from below by the sequence $(n)_{n\in \mathbb {N} }$ , which in turn diverges to $+\infty$ . So the series $\sum _{k=0}^{\infty }q^{k}$ must diverge, as well.

Conclusion

We have learned: for $|q|>1$ , $q=-1$ and $q=1$ , the geometric series diverges. These three cases can be concluded into one case $|q|\geq 1$ . However, if $|q|<1$ , then the geometric series converges to ${\tfrac {1}{1-q}}$ :

Theorem (geometric series)

The geometric series $\sum _{k=0}^{\infty }q^{k}$ converges if and only if $|q|<1$ . In that case, the limit is ${\tfrac {1}{1-q}}$ , or written in shorthand notation:

\sum _{k=0}^{\infty }q^{k}={\begin{cases}{\frac {1}{1-q}}&;|q|<1\\{\text{diverges}}&;|q|\geq 1\end{cases}}

Example (geometric series)

For $q={\tfrac {1}{2}}$ , $q=-{\tfrac {1}{2}}$ and $q=2$ there is

{\begin{aligned}\sum _{k=0}^{\infty }\left({\frac {1}{2}}\right)^{k}&=1+{\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{8}}+{\frac {1}{16}}+\ldots ={\frac {1}{1-{\frac {1}{2}}}}={\frac {1}{\frac {1}{2}}}=2\\[1em]\sum _{k=0}^{\infty }\left(-{\frac {1}{2}}\right)^{k}&=1-{\frac {1}{2}}+{\frac {1}{4}}-{\frac {1}{8}}+{\frac {1}{16}}-\ldots ={\frac {1}{1+{\frac {1}{2}}}}={\frac {1}{\frac {3}{2}}}={\frac {2}{3}}\\[1em]\sum _{k=0}^{\infty }2^{k}&=1+2+4+8+16+\ldots \ {\text{ diverges to }}+\infty \end{aligned}}

Example problems

Problem 1

Exercise (problems: geometric series)

Compute the values (=limits) of the following series:

$\sum _{k=0}^{\infty }{\frac {1}{3^{k}}}$
$\sum _{k=0}^{\infty }{\frac {2^{k}}{3^{k}}}$
$\sum _{k=0}^{\infty }{\frac {(-2)^{k}}{3^{k}}}$
$\sum _{k=1}^{\infty }{\frac {1}{2^{k}}}$
$\sum _{k=4}^{\infty }{\frac {1}{3^{k-2}}}$

Solution (problems: geometric series)

Solution sub-exercise 1:

{\begin{aligned}\sum _{k=0}^{\infty }{\frac {1}{3^{k}}}&=\sum _{k=0}^{\infty }{\frac {1^{k}}{3^{k}}}\\[0.5em]&=\sum _{k=0}^{\infty }\left({\frac {1}{3}}\right)^{k}\\[0.5em]&\quad {\color {OliveGreen}\left\downarrow \ \sum _{k=0}^{\infty }\left({\frac {1}{3}}\right)^{k}={\frac {1}{1-{\frac {1}{3}}}}={\frac {1}{\frac {2}{3}}}={\frac {3}{2}}\right.}\\[0.5em]&={\frac {3}{2}}\end{aligned}}

Solution sub-exercise 2:

{\begin{aligned}\sum _{k=0}^{\infty }{\frac {2^{k}}{3^{k}}}&=\sum _{k=0}^{\infty }\left({\frac {2}{3}}\right)^{k}\\[0.5em]&\quad {\color {OliveGreen}\left\downarrow \ \sum _{k=0}^{\infty }\left({\frac {2}{3}}\right)^{k}={\frac {1}{1-{\frac {2}{3}}}}={\frac {1}{\frac {1}{3}}}=3\right.}\\[0.5em]&=3\end{aligned}}

Solution sub-exercise 3:

{\begin{aligned}\sum _{k=0}^{\infty }{\frac {(-2)^{k}}{3^{k}}}&=\sum _{k=0}^{\infty }\left(-{\frac {2}{3}}\right)^{k}\\[0.5em]&\quad {\color {OliveGreen}\left\downarrow \ \sum _{k=0}^{\infty }\left(-{\frac {2}{3}}\right)^{k}={\frac {1}{1-(-{\frac {2}{3}})}}={\frac {1}{1+{\frac {2}{3}}}}={\frac {1}{\frac {5}{3}}}={\frac {3}{5}}\right.}\\[0.5em]&={\frac {3}{5}}\end{aligned}}

Solution sub-exercise 4:

{\tfrac {1}{2}}+{\tfrac {1}{4}}+{\tfrac {1}{8}}+\ldots =1

in a picture

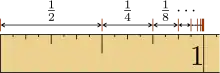
Careful! The series starts with $k=1$ and not $k=0$ . So we need to shuffle terms around first before we can apply the sum formula with $\sum _{k=0}^{\infty }$ :

{\begin{aligned}\sum _{k=1}^{\infty }{\frac {1}{2^{k}}}&=\left(\sum _{k=0}^{\infty }{\frac {1}{2^{k}}}\right)-{\frac {1}{2^{0}}}\\[0.5em]&=\left(\sum _{k=0}^{\infty }\left({\frac {1}{2}}\right)^{k}\right)-1\\[0.5em]&\quad {\color {OliveGreen}\left\downarrow \ \sum _{k=0}^{\infty }\left({\frac {1}{2}}\right)^{k}={\frac {1}{1-{\frac {1}{2}}}}=2\right.}\\[0.5em]&=2-1=1\end{aligned}}

Solution sub-exercise 5:

This series starts with $k=4$ . We perform an index shift to get it starting with $k=0$ :

{\begin{aligned}\sum _{k=4}^{\infty }{\frac {1}{3^{k-2}}}&{\underset {\text{shift}}{\overset {\text{index}}{=}}}\left(\sum _{k=2}^{\infty }{\frac {1}{3^{k}}}\right)\\[0.5em]&=\left(\sum _{k=0}^{\infty }{\frac {1}{3^{k}}}\right)-{\frac {1}{3^{0}}}-{\frac {1}{3^{1}}}\\[0.5em]&=\left(\sum _{k=0}^{\infty }\left({\frac {1}{3}}\right)^{k}\right)-1-{\frac {1}{3}}\\[0.5em]&\quad {\color {OliveGreen}\left\downarrow \ \sum _{k=0}^{\infty }\left({\frac {1}{3}}\right)^{k}={\frac {1}{1-{\frac {1}{3}}}}={\frac {3}{2}}\right.}\\[0.5em]&={\frac {3}{2}}-1-{\frac {1}{3}}\\[0.5em]&={\frac {1}{2}}-{\frac {1}{3}}\\[0.5em]&={\frac {3}{6}}-{\frac {2}{6}}={\frac {1}{6}}\end{aligned}}

Problem 2

Exercise (geometric series with special $q$ )

Let $M,N\in \mathbb {N}$ with $N\geq 2$ and $M<N$ . Find the limits of the following six geometric series:

$\sum _{k=0}^{\infty }{\frac {1}{N^{k}}}$ and $\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{N^{k}}}$
$\sum _{k=0}^{\infty }{\frac {M^{k}}{(M+1)^{k}}}$ and $\sum _{k=0}^{\infty }(-1)^{k}{\frac {M^{k}}{(M+1)^{k}}}$
$\sum _{k=0}^{\infty }{\frac {M^{k}}{N^{k}}}$ and $\sum _{k=0}^{\infty }(-1)^{k}{\frac {M^{k}}{N^{k}}}$

Solution (geometric series with special $q$ )

Solution sub-exercise 1:

{\begin{aligned}\sum _{k=0}^{\infty }{\frac {1}{N^{k}}}&=\sum _{k=0}^{\infty }\left({\frac {1}{N}}\right)^{k}\\[0.5em]&{\color {OliveGreen}\left\downarrow \ {\text{geometric series with }}q={\frac {1}{N}}\right.}\\[0.5em]&={\frac {1}{1-{\frac {1}{N}}}}={\frac {1}{\frac {N-1}{N}}}={\frac {N}{N-1}}\end{aligned}}

and

{\begin{aligned}\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{N^{k}}}&=\sum _{k=0}^{\infty }\left(-{\frac {1}{N}}\right)^{k}\\[0.5em]&{\color {OliveGreen}\left\downarrow \ {\text{geometric series with }}q=-{\frac {1}{N}}\right.}\\[0.5em]&={\frac {1}{1+{\frac {1}{N}}}}={\frac {1}{\frac {N+1}{N}}}={\frac {N}{N+1}}\end{aligned}}

Solution sub-exercise 2:

{\begin{aligned}\sum _{k=0}^{\infty }{\frac {M^{k}}{(M+1)^{k}}}&=\sum _{k=0}^{\infty }\left({\frac {M}{M+1}}\right)^{k}\\[0.5em]&{\color {OliveGreen}\left\downarrow \ {\text{geometric series with }}q={\frac {M}{M+1}}\right.}\\[0.5em]&={\frac {1}{1-{\frac {M}{M+1}}}}={\frac {1}{\frac {1}{M+1}}}=M+1\end{aligned}}

and

{\begin{aligned}\sum _{k=0}^{\infty }(-1)^{k}{\frac {M^{k}}{(M+1)^{k}}}&=\sum _{k=0}^{\infty }\left(-{\frac {M}{M+1}}\right)^{k}\\[0.5em]&{\color {OliveGreen}\left\downarrow \ {\text{geometric series with }}q=-{\frac {M}{M+1}}\right.}\\[0.5em]&={\frac {1}{1+{\frac {M}{M+1}}}}={\frac {1}{\frac {2M+1}{M+1}}}={\frac {M+1}{2M+1}}\end{aligned}}

Solution sub-exercise 3:

{\begin{aligned}\sum _{k=0}^{\infty }{\frac {M^{k}}{N^{k}}}&=\sum _{k=0}^{\infty }\left({\frac {M}{N}}\right)^{k}\\[0.5em]&{\color {OliveGreen}\left\downarrow \ {\text{geometric series with }}q={\frac {M}{N}}\right.}\\[0.5em]&={\frac {1}{1-{\frac {M}{N}}}}={\frac {1}{\frac {N-M}{N}}}={\frac {N}{N-M}}\end{aligned}}

and

{\begin{aligned}\sum _{k=0}^{\infty }(-1)^{k}{\frac {M^{k}}{N^{k}}}&=\sum _{k=0}^{\infty }\left(-{\frac {M}{N}}\right)^{k}\\[0.5em]&{\color {OliveGreen}\left\downarrow \ {\text{geometric series with }}q=-{\frac {M}{N}}\right.}\\[0.5em]&={\frac {1}{1+{\frac {M}{N}}}}={\frac {1}{\frac {N+M}{N}}}={\frac {N}{N+M}}\end{aligned}}

Problem 3

Exercise (index shifting)

Let $q\in \mathbb {R}$ with $|q|<1$ . Find the limits of the three geometric series

$\sum _{k=1}^{\infty }q^{k}$
$\sum _{k=2}^{\infty }q^{k}$
$\sum _{k=m}^{\infty }q^{k}$ for $m\in \mathbb {N}$

Solution (index shifting)

Solution sub-exercise 1:

{\begin{aligned}\sum _{k=1}^{\infty }q^{k}&=\left(\sum _{k=0}^{\infty }q^{k}\right)-q^{0}\\[0.5em]&=\left(\sum _{k=0}^{\infty }q^{k}\right)-1\\[0.5em]&\quad {\color {OliveGreen}\left\downarrow \ \sum _{k=0}^{\infty }q^{k}={\frac {1}{1-q}}\right.}\\[0.5em]&={\frac {1}{1-q}}-1\\[0.5em]&={\frac {1}{1-q}}-{\frac {1-q}{1-q}}\\[0.5em]&={\frac {1-(1-q)}{1-q}}\\[0.5em]&={\frac {q}{1-q}}\end{aligned}}

Solution sub-exercise 2:

{\begin{aligned}\sum _{k=2}^{\infty }q^{k}&=\left(\sum _{k=0}^{\infty }q^{k}\right)-q^{0}-q^{1}\\[0.5em]&=\left(\sum _{k=0}^{\infty }q^{k}\right)-1-q\\[0.5em]&\quad {\color {OliveGreen}\left\downarrow \ \sum _{k=0}^{\infty }q^{k}={\frac {1}{1-q}}\right.}\\[0.5em]&={\frac {1}{1-q}}-1-q\\[0.5em]&={\frac {1}{1-q}}-{\frac {1-q}{1-q}}-{\frac {q(1-q)}{1-q}}\\[0.5em]&={\frac {1-(1-q)-q(1-q)}{1-q}}\\[0.5em]&={\frac {1-1+q-q+q^{2}}{1-q}}\\[0.5em]&={\frac {q^{2}}{1-q}}\end{aligned}}

Solution sub-exercise 3:

For $|q|<1$ and $m\in \mathbb {N}$ there is

{\begin{aligned}\sum _{k=m}^{\infty }q^{k}&=\left(\sum _{k=0}^{\infty }q^{k}\right)-\sum _{k=0}^{m-1}q^{k}\\[0.5em]&\quad {\color {OliveGreen}\left\downarrow \ \sum _{k=0}^{\infty }q^{k}={\frac {1}{1-q}}{\text{ v }}\sum _{k=0}^{m-1}q^{k}={\frac {1-q^{m}}{1-q}}\right.}\\[0.5em]&={\frac {1}{1-q}}-{\frac {1-q^{m}}{1-q}}\\[0.5em]&={\frac {1-(1-q^{m})}{1-q}}\\[0.5em]&={\frac {1-1+q^{m}}{1-q}}\\[0.5em]&={\frac {q^{m}}{1-q}}\end{aligned}}

Problem 4

Exercise (Sequences which relate to the geometric series)

Solve the following three problems:

For all real $q\neq 1$ and $n\in \mathbb {N}$ , prove the limit $\sum _{k=0}^{n}(k+1)q^{k}={\frac {1-(n+2)q^{n+1}+(n+1)q^{n+2}}{(1-q)^{2}}}$ .
For all $q\in \mathbb {R}$ with $|q|<1$ , prove the limit $\sum _{k=0}^{\infty }(k+1)q^{k}={\frac {1}{(1-q)^{2}}}$ .
Find the limits of the series $\sum _{k=0}^{\infty }{\frac {k+1}{2^{k}}}$ and $\sum _{k=1}^{\infty }{\frac {k}{2^{k}}}$ .

Solution (Sequences which relate to the geometric series)

Solution sub-exercise 1:

For all $q\in \mathbb {R}$ and $n\in \mathbb {N}$ we have to establish

(1-q)^{2}\cdot \sum _{k=0}^{n}(k+1)q^{k}=1-(n+2)q^{n+1}+(n+1)q^{n+2}

the left-hand side is re-arranged as follows:

{\begin{aligned}(1-q)^{2}\cdot \sum _{k=0}^{n}(k+1)q^{k}&=(1-2q+q^{2})\cdot \sum _{k=0}^{n}(k+1)q^{k}\\[0.5em]&=(1-q-(q-q^{2}))\cdot \sum _{k=0}^{n}(k+1)q^{k}\\[0.5em]&=(1-q)\cdot \sum _{k=0}^{n}(k+1)q^{k}-(q-q^{2})\cdot \sum _{k=0}^{n}(k+1)q^{k}\\[0.5em]&=\sum _{k=0}^{n}(k+1)q^{k}-\sum _{k=0}^{n}(k+1)q^{k+1}-\left[\sum _{k=0}^{n}(k+1)q^{k+1}-\sum _{k=0}^{n}(k+1)q^{k+2}\right]\\[0.5em]&={\color {OliveGreen}1+2q+3q^{2}+4q^{3}+\ldots +nq^{n-1}+(n+1)q^{n}}\\[0.5em]&\quad {\color {Red}-q-2q^{2}-3q^{3}-\ldots -(n-1)q^{n-1}-nq^{n}-(n+1)q^{n+1}}\\[0.5em]&\quad -\left[{\color {OliveGreen}q+2q^{2}+3q^{3}+\ldots +(n-1)q^{n-1}+nq^{n}+(n+1)q^{n+1}}\right.\\[0.5em]&\qquad \left.{\color {Red}-q^{2}-2q^{3}-\ldots -(n-2)q^{n-1}-(n-1)q^{n}-nq^{n+1}-(n+1)q^{n+2}}\right]\\[0.5em]&=1+q+q^{2}+q^{3}+\ldots +q^{n-1}+q^{n}-(n+1)q^{n+1}\\[0.5em]&\quad -[q+q^{2}+q^{3}+\ldots +q^{n-1}+q^{n}+q^{n+1}-(n+1)q^{n+2}]\\[0.5em]&{\color {OliveGreen}\left\downarrow \ {\text{telescoping sum}}\right.}\\[0.5em]&=1-(n+2)q^{n+1}+(n+1)q^{n+2}\end{aligned}}

Solution sub-exercise 2:

In the chapter Beispiele von Grenzwerten , we proved that $\lim _{n\to \infty }nq^{n}=0$ holds for $|q|<1$ (reason: $q^{n}$ grows exponentially and "beats" the linearly growing $n$ ). The limit theorems hence yield $\lim _{n\to \infty }nq^{n+1}=q\cdot \lim _{n\to \infty }nq^{n}=0$ and $\lim _{n\to \infty }(n+1)q^{n+2}=0$ . Therefore

{\begin{aligned}\sum _{k=0}^{\infty }(k+1)q^{k}&=\lim _{n\to \infty }\sum _{k=0}^{n}(k+1)q^{k}\\[0.5em]&=\lim _{n\to \infty }{\frac {1-(n+2)q^{n+1}+(n+1)q^{n+2}}{(1-q)^{2}}}\\[0.5em]&{\color {OliveGreen}\left\downarrow \ {\text{limit theorems}}\right.}\\[0.5em]&={\frac {1-\lim _{n\to \infty }(n+2)q^{n+1}+\lim _{n\to \infty }(n+1)q^{n+2}}{(1-q)^{2}}}\\[0.5em]&={\frac {1-0+0}{(1-q)^{2}}}\\[0.5em]&={\frac {1}{(1-q)^{2}}}\end{aligned}}

Solution sub-exercise 3:

We re-use the solution to sub-exercise 2 with $q={\tfrac {1}{2}}$ :

{\begin{aligned}\sum _{k=0}^{\infty }{\frac {k+1}{2^{k}}}&=\sum _{k=0}^{\infty }(k+1)\left({\frac {1}{2}}\right)^{k}\\[0.5em]&{\color {OliveGreen}\left\downarrow \ {\text{sub-exercise 2}}\right.}\\[0.5em]&={\frac {1}{(1-{\frac {1}{2}})^{2}}}\\[0.5em]&={\frac {1}{({\frac {1}{2}})^{2}}}={\frac {1}{\frac {1}{4}}}=4\end{aligned}}

The second limit also follows from $q={\tfrac {1}{2}}$ , using an index shift:

{\begin{aligned}\sum _{k=1}^{\infty }{\frac {k}{2^{k}}}&{\underset {\text{shift}}{\overset {\text{index-}}{=}}}\sum _{k=0}^{\infty }(k+1)\left({\frac {1}{2}}\right)^{k+1}\\[0.5em]&=\sum _{k=0}^{\infty }(k+1)\left({\frac {1}{2}}\right)^{k}{\frac {1}{2}}\\[0.5em]&={\frac {1}{2}}\sum _{k=0}^{\infty }(k+1)\left({\frac {1}{2}}\right)^{k}\\[0.5em]&{\color {OliveGreen}\left\downarrow \ {\text{sub-exercise 2}}\right.}\\[0.5em]&={\frac {1}{2}}{\frac {1}{(1-{\frac {1}{2}})^{2}}}\\[0.5em]&={\frac {1}{2}}{\frac {1}{\frac {1}{4}}}={\frac {4}{2}}=2\end{aligned}}

Solution (Alternative proof to sub-exercise 1)

We may also reconstruct the limit in a similar manner to the geometric sum formula: There is a factor of $(1-q)^{2}$ in the denominator, so applying the trick "multiply by $q$ and subtract" twice, we should get to the result. We start from

\sum _{k=0}^{n}(k+1)q^{k}=\ 1+2q+3q^{2}+4q^{3}+5q^{4}+\ldots +nq^{n-1}+(n+1)q^{n}

And multiply the equation by $q$ :

q\cdot \sum _{k=0}^{n}(k+1)q^{k}=\ q+2q^{2}+3q^{3}+4q^{4}+5q^{5}+\ldots +nq^{n}+(n+1)q^{n+1}

Next, both results are subtracted:

{\begin{aligned}\sum _{k=0}^{n}(k+1)q^{k}-q\cdot \sum _{k=0}^{n}(k+1)q^{k}&=(1+2q+3q^{2}+4q^{3}+\ldots +nq^{n-1}+(n+1)q^{n})\\[0.5em]&\quad -(q+2q^{2}+3q^{3}+4q^{4}+\ldots +nq^{n}+(n+1)q^{n+1})\\[0.5em]&=1+q+q^{2}+q^{3}+\ldots +q^{n-1}+q^{n}-(n+1)q^{n+1}\\[0.5em]\end{aligned}}

On the left side, we may factor out a second $(1-q)$ :

{\begin{aligned}(1-q)\cdot \sum _{k=0}^{n}(k+1)q^{k}&=\ 1+q+q^{2}+q^{3}+\ldots +q^{n-1}+q^{n}-(n+1)q^{n+1}\\[0.5em]&{\color {OliveGreen}\left\downarrow \ {}\cdot {\frac {1}{1-q}}\right.}\\[0.5em]\implies \ \sum _{k=0}^{n}(k+1)q^{k}&=\ {\frac {1+q+q^{2}+q^{3}+\ldots +q^{n-1}+q^{n}-(n+1)q^{n+1}}{1-q}}\\[0.5em]&{\color {OliveGreen}\left\downarrow \ {\text{expand by }}1-q{\text{ and multiply out}}\right.}\\[0.5em]&=\ {\frac {1-(n+2)q^{n+1}+(n+1)q^{n+2}}{(1-q)^{2}}}\\[0.5em]\end{aligned}}

Solution (Alternative proof to sub-exercise 3)

We may also add and subtract a 1:

{\begin{aligned}\sum _{k=1}^{\infty }{\frac {k}{2^{k}}}&=\sum _{k=0}^{\infty }k\left({\frac {1}{2}}\right)^{k}\\[0.5em]&=\sum _{k=0}^{\infty }(k+1-1)\left({\frac {1}{2}}\right)^{k}\\[0.5em]&{\color {OliveGreen}\left\downarrow \ {\text{series }}\sum _{k=0}^{\infty }(k+1)\left({\frac {1}{2}}\right)^{k}{\text{ and }}\sum _{k=0}^{\infty }\left({\frac {1}{2}}\right)^{k}{\text{ converge}}\right.}\\[0.5em]&=\sum _{k=0}^{\infty }(k+1)\left({\frac {1}{2}}\right)^{k}-\sum _{k=0}^{\infty }\left({\frac {1}{2}}\right)^{k}\\[0.5em]&{\color {OliveGreen}\left\downarrow \ {\text{sub-exercise 2 with }}q={\tfrac {1}{2}}\right.}\\[0.5em]&={\frac {1}{(1-{\frac {1}{2}})^{2}}}-\sum _{k=0}^{\infty }\left({\frac {1}{2}}\right)^{k}\\[0.5em]&{\color {OliveGreen}\left\downarrow \ {\text{geometric series}}\right.}\\[0.5em]&={\frac {1}{(1-{\frac {1}{2}})^{2}}}-{\frac {1}{1-{\frac {1}{2}}}}\\[0.5em]&={\frac {1}{\frac {1}{4}}}-{\frac {1}{\frac {1}{2}}}=4-2=2\end{aligned}}

Hint

Analogously to sub-exercise 3, one may show for every $|q|<1$ that:

\sum _{k=1}^{\infty }kq^{k}={\frac {q}{(1-q)^{2}}}

just replace ${\tfrac {1}{2}}$ by $q$

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

Geometric sum formula

Geometric series

Case | q | < 1 {\displaystyle |q|<1}

Case | q | ≥ 1 {\displaystyle |q|\geq 1}

Conclusion

Example problems

Problem 1

Problem 2

Problem 3

Problem 4

Case $|q|<1$

Case $|q|\geq 1$