Näherungskonstruktion der Ecke 1.024

01-65537-Eck E-17 o. Hinweise

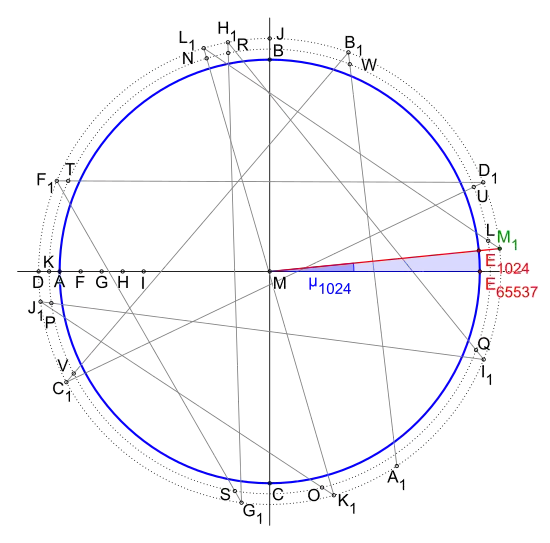
1. Bestimme die Lage des Mittelpunktes M
2. Zeichne einen Kreis, den Umkreis des späteren 65537-Ecks, um den Mittelpunkt M mit einem beliebigen Radius.
3. Zeichne zwei zueinander senkrecht stehende Mittelachsen, damit ergeben sich auf dem Umkreis die Punkte A, E₆₅₅₃₇ bzw. B und C.
4. Konstruiere auf der Mittelachse AE₆₅₅₃₇ außerhalb des Kreises die Strecke AD, sie ist ein Zehntel der Strecke AM.
5. Trage die Strecke AD ab dem Punkt A viermal auf die Mittelachse AE₆₅₅₃₇ ab, damit ergeben sich die Punkte F, G, H und I.
6. Zeichne den Hilfskreis mit dem Radius MD um den Punkt M, er wird im Folgenden Hilfskreis durch D genannt; der Schnittpunkt mit der Mittelachse BC ist J.
7. Halbiere die Strecke AD, damit ergibt sich der Punkt K.
8. Zeichne den Hilfskreis mit dem Radius MK um den Punkt M; dieser Hilfskreis wird im Folgenden Hilfskreis durch K genannt.
9. Bestimme auf dem Hilfskreis durch K den Punkt L mit einem Abstand |E₆₅₅₃₇L|, der gleich lang ist wie die Strecke FK.
10. Bestimme auf dem Hilfskreis durch K den Punkt N mit einem Abstand |BN|, der gleich lang ist wie die Strecke AH.
11. Bestimme auf dem Hilfskreis durch K den Punkt O mit einem Abstand |CO|, der gleich lang ist wie die Strecke GK.
12. Bestimme auf dem Hilfskreis durch K den Punkt P mit einem Abstand |KP|, der gleich lang ist wie die Strecke FK.
13. Bestimme auf dem Hilfskreis durch K den Punkt Q mit einem Abstand |CQ|, der gleich lang ist wie der Abstand |CI|.
14. Bestimme auf dem Hilfskreis durch K den Punkt R mit einem Abstand |BR|, der gleich lang ist wie die Strecke AG.
15. Bestimme auf dem Hilfskreis durch K den Punkt S mit einem Abstand |HS|, der gleich lang ist wie der Abstand |BI|.
16. Bestimme auf dem Hilfskreis durch K den Punkt T mit einem Abstand |DT|, der gleich lang ist wie die Strecke IK.
17. Bestimme auf dem Hilfskreis durch K den Punkt U mit einem Abstand |E₆₅₅₃₇U|, der gleich lang ist wie die Strecke AI.
18. Bestimme auf dem Hilfskreis durch K den Punkt V mit einem Abstand |GV|, der gleich lang ist wie die Strecke DI.
19. Bestimme auf dem Hilfskreis durch K den Punkt W mit einem Abstand |JW|, der gleich lang ist wie die Strecke AI.
20. Bestimme auf dem Hilfskreis durch D den Punkt A₁ mit einem Abstand |E₆₅₅₃₇A₁|, der gleich lang ist wie die Strecke MA.
21. Zeichne ab dem Punkt A₁ eine gerade Linie durch den Punkt W, damit ergibt sich der Schnittpunkt B₁ auf dem Hilfskreis durch D.
22. Zeichne ab dem Punkt B₁ eine gerade Linie durch den Punkt V, damit ergibt sich der Schnittpunkt C₁ auf dem Hilfskreis durch D.
23. Zeichne ab dem Punkt C₁ eine gerade Linie durch den Punkt U, damit ergibt sich der Schnittpunkt D₁ auf dem Hilfskreis durch D.
24. Zeichne ab dem Punkt D₁ eine gerade Linie durch den Punkt T, damit ergibt sich der Schnittpunkt F₁ auf dem Hilfskreis durch D.
25. Zeichne ab dem Punkt F₁ eine gerade Linie durch den Punkt S, damit ergibt sich der Schnittpunkt G₁ auf dem Hilfskreis durch D.
26. Zeichne ab dem Punkt G₁ eine gerade Linie durch den Punkt R, damit ergibt sich der Schnittpunkt H₁ auf dem Hilfskreis durch D.
27. Zeichne ab dem Punkt H₁ eine gerade Linie durch den Punkt Q, damit ergibt sich der Schnittpunkt I₁ auf dem Hilfskreis durch D.
28. Zeichne ab dem Punkt I₁ eine gerade Linie durch den Punkt P, damit ergibt sich der Schnittpunkt J₁ auf dem Hilfskreis durch D.
29. Zeichne ab dem Punkt J₁ eine gerade Linie durch den Punkt O, damit ergibt sich der Schnittpunkt K₁ auf dem Hilfskreis durch D.
30. Zeichne ab dem Punkt K₁ eine gerade Linie durch den Punkt N, damit ergibt sich der Schnittpunkt L₁ auf dem Hilfskreis durch D.
31. Zeichne ab dem Punkt L₁ eine gerade Linie durch den Punkt L, damit ergibt sich der Schnittpunkt M₁ auf dem Hilfskreis durch D.
32. Verbinde den Punkt M₁ mit dem Mittelpunkt M, auf dem Umkreis ergibt sich somit annähernd die Ecke E₁₀₂₄, d. h. der Kreisbogen ME₆₅₅₃₇E₁₀₂₄ beinhaltet annähernd 1024 Seiten des regelmäßigen 65537-Ecks.

Näherungskonstruktion der ersten Seite

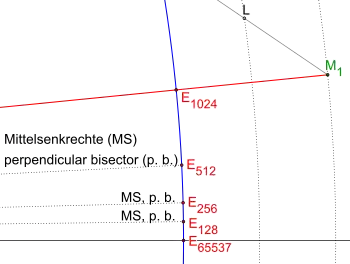65537-Eck, 1. Vergrößerung Erzeuge eine stark vergrößerte Ansicht des Kreisbogens ${\displaystyle ME_{65537}E_{1024}}$ und halbiere mittels MS dreimal den Winkel ${\displaystyle E_{65537}ME_{1024}}$, ergibt die Ecken ${\displaystyle E_{512},E_{256}}$ und ${\displaystyle E_{128}}$

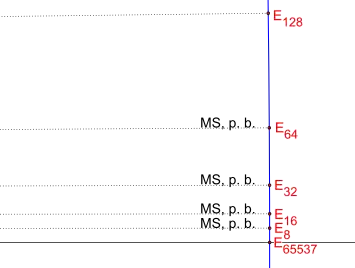65537-Eck, 2. Vergrößerung Erzeuge eine stark vergrößerte Ansicht des Kreisbogens ${\displaystyle ME_{65537}E_{128}}$ und halbiere mittels MS viermal den Winkel ${\displaystyle E_{65537}ME_{128}}$, ergibt die Ecken ${\displaystyle E_{64},E_{32},E_{16}}$ und ${\displaystyle E_{8}}$

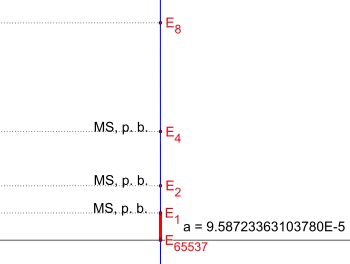65537-Eck, 3. Vergrößerung Erzeuge eine stark vergrößerte Ansicht des Kreisbogens ${\displaystyle ME_{65537}E_{8}}$ und halbiere mittels MS dreimal den Winkel ${\displaystyle E_{65537}ME_{8}}$, ergibt die Ecken ${\displaystyle E_{4},E_{2}}$ und ${\displaystyle E_{1}}$

In der dritten Vergrößerung, ergibt sich somit annähernd die erste Seite E₆₅₅₃₇E₁ = a des regelmäßigen 65537-Ecks.

Ergebnis

• Konstruierter Winkel (Anzeige GeoGbra) ${\displaystyle \mu _{1024}=5{,}62491417062117^{\circ }}$
• Winkel ${\displaystyle \mu _{1024\;SOLL}=360^{\circ }\cdot {\frac {1024}{65537}}=5{,}62491417062118...^{\circ }}$
• Absoluter Fehler des konstruierten Winkels ${\displaystyle F_{\mu 1024}=\mu _{1024}-\mu _{1024\;SOLL}=-1E-14^{\circ }}$

(1 Winkelsekunde = ${\displaystyle {\frac {1^{\circ }}{3600}}}$ = 0,000277...° = 2,77...E-4°)

• Konstruierte Seite des 65537-Ecks (Anzeige GeoGbra) ${\displaystyle a={\overline {E_{65537}E_{1}}}=9{,}58723363103780E-5\;[LE]}$
• Seite des 65537-Ecks ${\displaystyle a_{SOLL}=2\cdot \sin \left({\frac {180^{\circ }}{65537}}\right)=9{,}5872336310378200E-5\;[LE]}$
• Absoluter Fehler der konstruierten ersten Seite ${\displaystyle F_{a}=a-a_{SOLL}=-2E-19\;[LE]}$
• Absoluter Fehler der letzten Seite ${\displaystyle F_{a65537}=-F_{a}\cdot 65537=2E-19\cdot 65537=1{,}31074E-14\;[LE]}$

• Konstruierter Zentriwinkel (Anzeige GeoGbra) ${\displaystyle \mu =5{,}49308024474723E-3^{\circ }}$
• Zentriwinkel ${\displaystyle \mu _{SOLL}={\frac {360^{\circ }}{65537}}=5{,}4930802447472420E-3^{\circ }}$
• Absoluter Fehler vom konstruierten Zentriwinkel ${\displaystyle F_{\mu }=\mu -\mu _{SOLL}=-1{,}2...E-17^{\circ }}$

Beispiel um den Fehler zu verdeutlichen

Bei einem Umkreisradius r = 10 Billionen km (das Licht bräuchte für diese Strecke ca. 1 Jahr und 21 Tage) wäre die 1. Seite ca. 2 mm zu kurz, bzw. die 65537. Seite ca. 131 m zu lang.