natürliche Zahlen

${\displaystyle \mathbb {N} =\{1,2,3,\dots \}=\{k\}_{k=1}^{\infty }}$

Die Menge der natürlichen Zahlen ist eine ideale Indexmenge und wird für Abzählbarkeitsaussagen verwendet.

Menge der natürlichen Zahlen einschließlich der "Null": ${\displaystyle \mathbb {N} _{0}=\{0,1,2,3,\dots \}=\{0\}\cup \mathbb {N} }$

Axiomatik der natürlichen Zahlen

(N1)	Die Zahl "1" ist eine natürliche Zahl: ${\displaystyle 1\in \mathbb {N} }$
(N2)	Ist n eine natürliche Zahl, so ist auch (n + 1) eine natürliche Zahl: ${\displaystyle n\in \mathbb {N} \Rightarrow (n+1)\in \mathbb {N} }$
Definition	(n + 1) heißt der Nachfolger von n und n nennt man den Vorgänger von (n + 1)
(N3)	Jede Menge M die die Zahl "1" und mit n auch stehts die Zahl (n + 1) enthält ist gleich der Menge der natürlichen Zahlen (${\displaystyle M=\mathbb {N} }$) (Induktionsaxiom)

ganze Zahlen

${\displaystyle \mathbb {Z} =\{\dots -2,-1,0,1,2\dots \}=-\mathbb {N} \cup \mathbb {N} _{0}}$

${\displaystyle -\mathbb {N} :=\{(-1)\cdot x:x\in \mathbb {N} \}}$

rationale Zahlen

Die Menge der rationalen Zahlen ist die Menge aller Zahlen die sich als Bruch aus ganzen Zahlen darstellen lassen.

${\displaystyle \mathbb {Q} =\left\{x\left|x={\frac {p}{q}},p\in \mathbb {Z} ,q\in \mathbb {N} \right\}\right.}$

Der Fall ${\displaystyle q=0}$ ist per Definition ausgeschlossen.

irrationale Zahlen

Die Menge der irrationalen Zahlen ist die Menge aller nichtendlichen und nichtperiodischen Dezimalbrüche.
Beispiele: ${\displaystyle {\sqrt {2}},\pi ,e}$

reelle Zahlen

Zahlenstrahl zur Darstellung der Reellen Zahlen

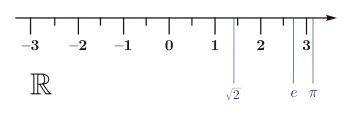
Die Menge der reellen Zahlen bezeichnet die Menge aller Zahlen, die sich durch einen (unendlichen) Dezimalbruch darstellen lassen.

${\displaystyle \mathbb {R} =\left\{x:x=p,p_{1}p_{2}p_{3}\dots {\mbox{ mit }}{\begin{matrix}p\in \mathbb {Z} \\p_{k}\in \{k\}_{k=0}^{9}\\k\in \mathbb {N} \end{matrix}}\right\}}$

komplexe Zahlen

${\displaystyle \mathbb {C} =\left\{z:z=a+i\cdot b{\mbox{ mit }}{\begin{matrix}a,b\in \mathbb {R} \\i^{2}=-1\end{matrix}}\right\}}$

Dabei wird ${\displaystyle a={\mbox{Re}}(z)}$ als Realteil und ${\displaystyle b={\mbox{Im }}(z)}$ als Imaginärteil von z bezeichnet.

Beziehungen zwischen Mengen

Im Sinne der Mengeninklusion gilt:

${\displaystyle \mathbb {N} \subset \mathbb {N} _{0}\subset \mathbb {Z} \subset \mathbb {Q} \subset \mathbb {R} \subset \mathbb {C} }$